Транспортная задача на сети

ТРАНСПОРТНАЯ ЗАДАЧА НА СЕТИ

ТРАНСПОРТНАЯ ЗАДАЧА НА СЕТИ
Существуют два наиболее распространенных метода решения транспортной задачи в сетевой форме:
метод сокращения невязок или условно оптимальных планов;
метод последовательного улучшения плана (метод потенциалов).
Рассмотрим решение сетевой транспортной задачи без учета ограничений пропускной способности методом последовательного улучшения плана. В этом случае математическая постановка задачи должна быть сформулирована без учета условия (3).

ТРАНСПОРТНАЯ ЗАДАЧА НА СЕТИ
Далее осуществим пошаговые действия для решения задачи.
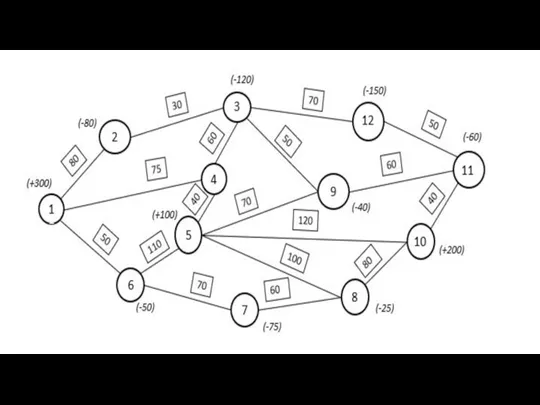
Шаг 1 — составим начальный план, в котором весь груз должен быть отправлен и все потребности станций прибытия удовлетворены. Стрелками обозначим направление грузопотоков, а числами — их мощность.
Шаг 2 — присвоим вершинам соответствующие потенциалы. Условия оптимальности плана такие же, как и при решении задачи в матричной форме методом потенциалов:

ТРАНСПОРТНАЯ ЗАДАЧА НА СЕТИ

ТРАНСПОРТНАЯ ЗАДАЧА НА СЕТИ
Для начала одной из вершин, например 1, зададим любой потенциал, достаточно большой, чтобы не иметь дело с отрицательными числами (в нашей задаче 100). Продвигаясь по дугам в направлении следования грузопотока, прибавляем к потенциалу предыдущей вершины величину стоимости звена; при движении против потока стоимость из потенциала вычитаем.
Потенциал вершины 2 = 100 + 80 = 180;
3 = 180 + 30 = 210;
4 = 210–60 = 150;
5 = 150–40 = 110.
Продолжаем это до тех пор, пока потенциалы не будут присвоены всем вершинам сети (рис. 3).

ТРАНСПОРТНАЯ ЗАДАЧА НА СЕТИ

ТРАНСПОРТНАЯ ЗАДАЧА НА СЕТИ
Проверяем условия оптимальности плана (6) на всех дугах без потока. Нарушения запишем против соответствующей дуги со знаком «+». В нашей задаче условия (6) нарушены на дугах 5.8 (+60) и 6.7 (+110) (рис. 3).

ТРАНСПОРТНАЯ ЗАДАЧА НА СЕТИ
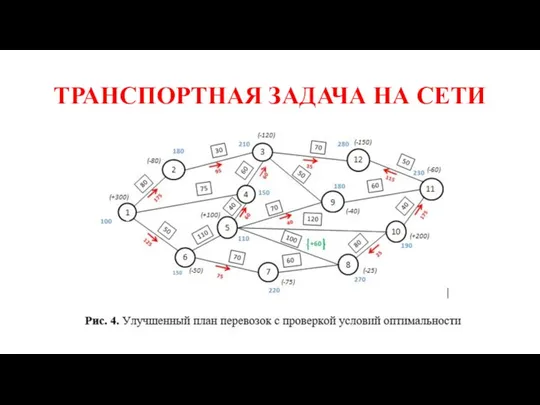
ШАГ 3. Выбираем дугу 6.7 с наибольшим нарушением. Величина его положительна, следовательно, необходимо направить грузопоток в направлении от меньшего потенциала к большему. Находим замкнутый контур, состоящий из дуг с потоком и выбранной дуги с нарушением. Это можно сделать единственным образом. В нашей задаче он состоит из дуг 6.7, 7.8, 8.10, 10.11, 11.12, 12.3, 3.2, 2.1, 1.6. Продвигаясь по контуру в направлении от меньшего потенциала дуги с нарушением к большем, в нашем случае против часовой стрелки, находим дугу 7.8 с минимальным встречным грузопотоком — 75 единиц. Прибавляем их ко всем попутным потокам и вычитаем из всех встречных. Улучшенный план показан на рис. 4.

ТРАНСПОРТНАЯ ЗАДАЧА НА СЕТИ

ТРАНСПОРТНАЯ ЗАДАЧА НА СЕТИ
Шаги 2 и 3 поочередно повторяют до тех пор, пока не будет дуг с нарушением условий (6).В дальнейшем при шаге 2 не требуется вновь присваивать потенциалы, достаточно исправить их у тех вершин сети, куда грузопоток подошел с другого направления.
После исправления плана осталось нарушение на дуге 5.8. Замкнутый контур состоит теперь из дуг 5.8, 8.10, 10.11, 11.12, 12.3, 3.4, 4.5. Направление движения — против часовой стрелки. Минимальный встречный поток равен 25 на дуге 8.10. Оптимальный план показан на рис. 5.

ТРАНСПОРТНАЯ ЗАДАЧА НА СЕТИ

ТРАНСПОРТНАЯ ЗАДАЧА НА СЕТИ
Нарушений условий (6) ни на одной дуге нет. За две итерации получена экономия по сравнению с начальным планом 110 × 75+60 × 25 = 9750 единиц стоимости (например, тонно-километров).
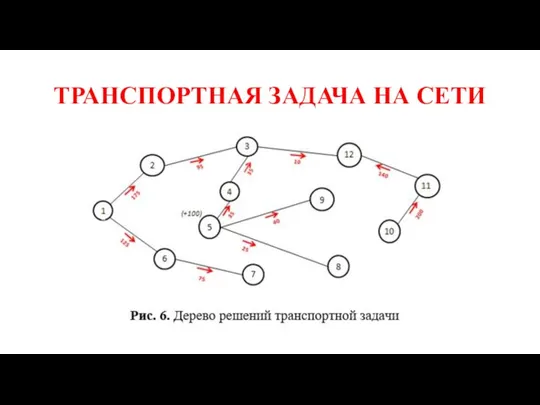
Представим на рис. 6 только те дуги, по которым проходят грузопотоки. Эта часть сети не содержит ни одного замкнутого контура и является деревом решения (дерево — одно из определяющих понятий в теории графов).

ТРАНСПОРТНАЯ ЗАДАЧА НА СЕТИ