Центральне розтягання (стискання) стержня

Поздовжні сили при розтяганні (стисканні) та їхнє визначення
Центральним розтяганням (центральним стисканням) називають такий вид деформації, коли в поперечному перерізі стержня з шести можливих внутрішніх силових факторів виникає лише один - поздовжня сила N. Для визначення поздовжніх сил у стержні використовують метод перерізів (рис. 1).
Рис. 1
Для перерізу І – І рівняння рівноваги
Для перерізу ІІ – ІІ рівняння рівноваги
Поздовжня сила в даному поперечному перерізі дорівнює сумі проекцій усіх зовнішніх сил, розташованих з одного боку від цього перерізу, на вісь, паралельну до осі стержня.
Поздовжня сила, яка викликає розтягання, спрямована від перерізу є додатною, а поздовжня сила, яка викликає стискання, спрямована до перерізу є від’ємною. В тому разі, коли напрям поздовжньої сили заздалегідь невідомий, її спрямовують від перерізу. Якщо з рівнянь рівноваги поздовжня сила отримана зі знаком плюс, то стержень розтягнутий, якщо зі знаком мінус – то стиснутий.
2

.
2. Напруження в поперечних і в похилих перерізах стержня при розтяганні (стисканні)
Напруження у поперечному перерізі стержня
Поздовжня сила N, що виникає в поперечному перерізі стержня, є рівнодійною внутрішніх нормальних зусиль, розподілених по площі поперечного перерізу А. Зв’язок поздовжньої сили з нормальними напруженнями σ, які виникають у цьому перерізі, виражають так
За умови виконання гіпотези плоских перерізів:
Це дозволяє у формулі (1) напруження винести за знак інтеграла
(1)
(2)
(3)
З формули (2) маємо нормальне напруження у поперечному перерізі.:
3

4
Напруження у довільному похилому перерізі стержня
Рис. 2
- зовнішня нормаль до похилого перерізу (рис. 2).
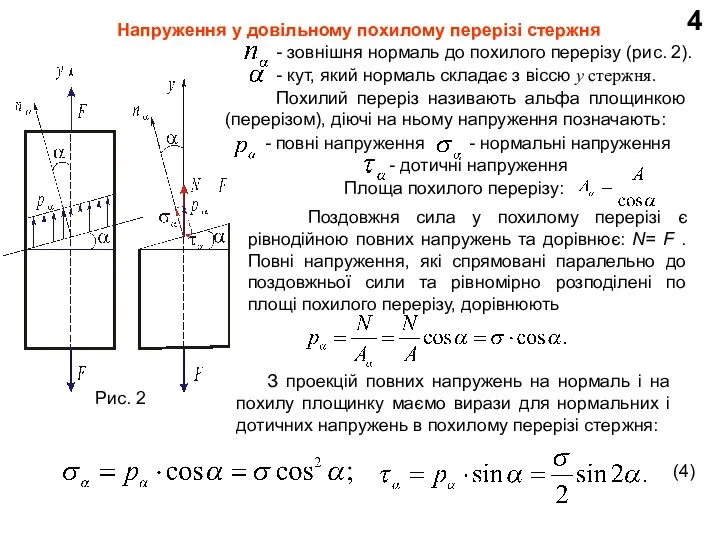
- кут, який нормаль складає з віссю у стержня.
Похилий переріз називають альфа площинкою (перерізом), діючі на ньому напруження позначають:
- повні напруження
- нормальні напруження
- дотичні напруження
Поздовжня сила у похилому перерізі є рівнодійною повних напружень та дорівнює: N= F . Повні напруження, які спрямовані паралельно до поздовжньої сили та рівномірно розподілені по площі похилого перерізу, дорівнюють
Площа похилого перерізу:
З проекцій повних напружень на нормаль і на похилу площинку маємо вирази для нормальних і дотичних напружень в похилому перерізі стержня:
(4)

5
З аналізу співвідношень (4) випливає:
1. У похилих перерізах розтягнутого (стиснутого) стержня діють водночас як нормальні так і дотичні напруження, величина яких залежить від кута α нахилу площинки перерізу.
2. Максимальні нормальні напруження є тоді, коли α=0, тобто в поперечних перерізах стержня.
3. Максимальні дотичні напруження діють на площинках, нахилених до осі стержня під кутом α=450
Напруження у довільному похилому перерізі стержня
4. Нормальні напруження на цих площинках дорівнюють дотичним, тобто

6
3. Поздовжні та поперечні деформації при розтяганні (стисканні). Закон Гука
Експерименти показують, що в результаті розтягання стержня його поздовжній розмір збільшується, а поперечний – зменшуються (рис. 3), при стисканні - навпаки.
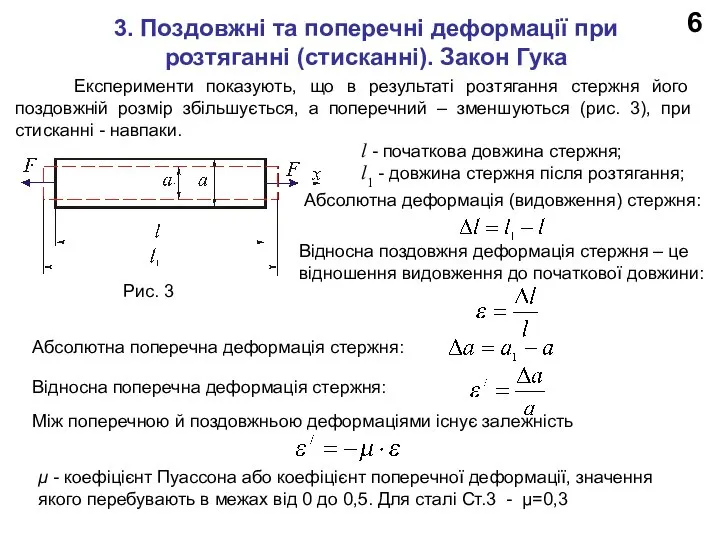
Рис. 3
l - початкова довжина стержня;
l1 - довжина стержня після розтягання;
Абсолютна деформація (видовження) стержня:
Відносна поздовжня деформація стержня – це відношення видовження до початкової довжини:
Абсолютна поперечна деформація стержня:
Відносна поперечна деформація стержня:
Між поперечною й поздовжньою деформаціями існує залежність
μ - коефіцієнт Пуассона або коефіцієнт поперечної деформації, значення якого перебувають в межах від 0 до 0,5. Для сталі Ст.3 - μ=0,3

7
Закон Гука
(5)
Експериментально встановлено, що відносна поздовжня деформація прямо пропорційна нормальному напруженню: Співвідношення (5) є математичним записом закону Гука. Характеристикою пружних властивостей матеріалу є величина Е - модуль пружності першого роду або модуль Юнга; для сталі Ст3:
Якщо врахувати вирази: для напружень (2), відносної поздовжньої деформації і закон Гука (5), то для абсолютної деформації стержня отримаємо формулу Гука:
Добуток ЕА в знаменнику формули Гука має розмірність сили. Цей добуток називають жорсткістю поперечного перерізу стержня при розтяганні (стисканні). Формулу (6) можна застосовувати лише для окремої ділянки стержня, що має постійний поперечний переріз і величина N у межах цієї ділянки стержня не змінюється. Для стержня змінного (ступінчастого) перерізу, видовження визначають на кожній характерній ділянці, а потім сумують, так що загальне видовження (вкорочення) обчислюють за формулою:
(6)
(7)
Якщо стержень розтягується силою та нагрівається, його деформація дорівнює

8
4. Епюра поздовжньої сили при розтяганні (стисканні)
N1 = F1= 40 кН;
N2 = F1 – F2= 40 – 60 = - 20 кН.
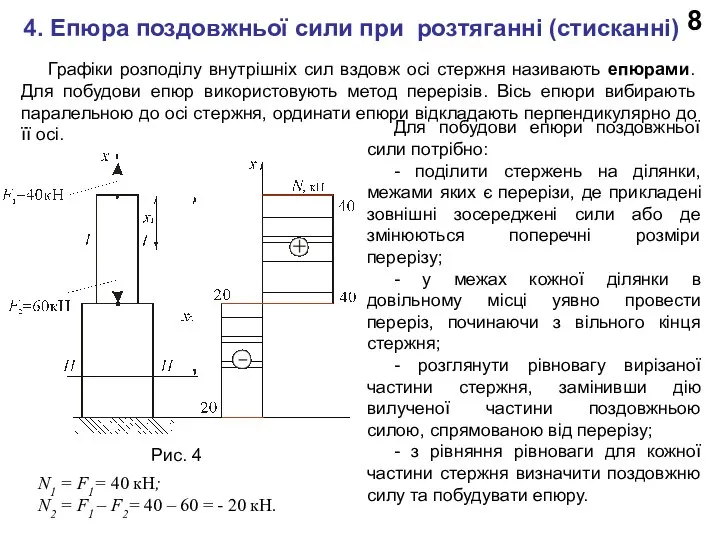
Рис. 4
Графіки розподілу внутрішніх сил вздовж осі стержня називають епюрами. Для побудови епюр використовують метод перерізів. Вісь епюри вибирають паралельною до осі стержня, ординати епюри відкладають перпендикулярно до її осі.
Для побудови епюри поздовжньої сили потрібно:
- поділити стержень на ділянки, межами яких є перерізи, де прикладені зовнішні зосереджені сили або де змінюються поперечні розміри перерізу;
- у межах кожної ділянки в довільному місці уявно провести переріз, починаючи з вільного кінця стержня;
- розглянути рівновагу вирізаної частини стержня, замінивши дію вилученої частини поздовжньою силою, спрямованою від перерізу;
- з рівняння рівноваги для кожної частини стержня визначити поздовжню силу та побудувати епюру.