Содержание
- 2. Содержание Введение Случайные возмущения Классическое Броуновское движение Срединные смещения Срединное смещение и ФБД Фурье-анализ ФБД. Фильтрация
- 3. Фракталы, получаемые с помощью L-систем или СИФ, обладают одним явным недостатком, ограничивающим их применение для моделирования
- 4. Случайные возмущения Рис. 1. Рандомизированная снежинка Коха. Рис. 2. Рандомизированный ковер Серпинского.
- 5. Броуновское движение
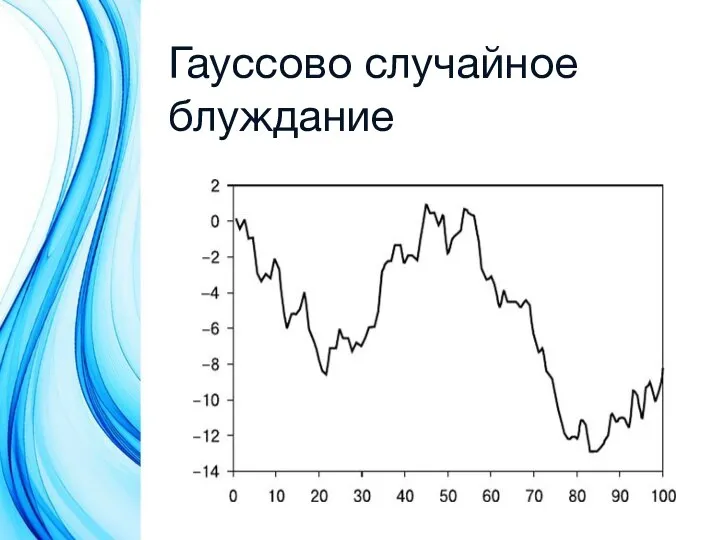
- 6. Гауссово случайное блуждание
- 7. Гауссово случайное блуждание
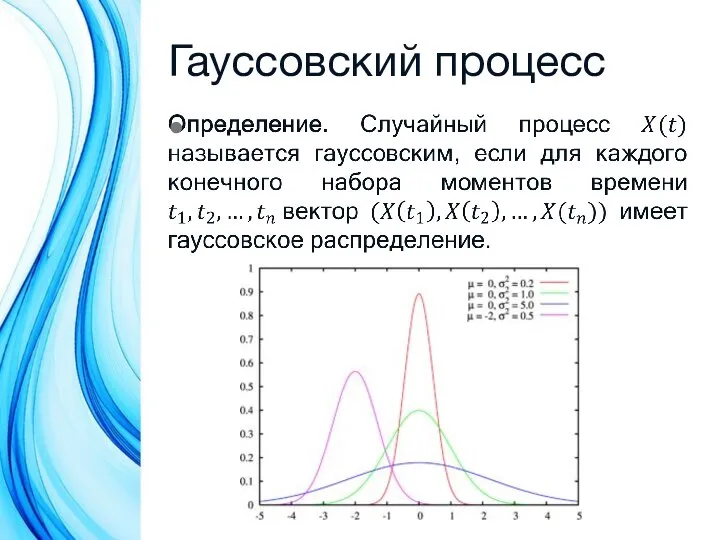
- 8. Гауссовский процесс
- 9. Классическое броуновское движение
- 10. Свойства
- 11. Теоремы
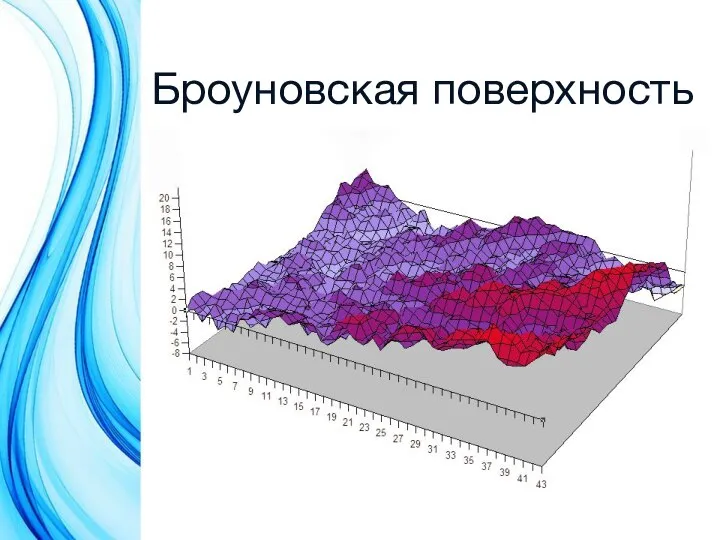
- 12. Броуновская поверхность
- 13. Срединные смещения. Кривая A B C D E A B C
- 14. Срединные смещения. Поверхность
- 15. Фрактальное броуновское движение
- 16. Свойства
- 17. Теоремы
- 18. Фурье-анализ ФБД
- 19. Оценка спектральной плотности ФБД
- 20. Определение ДПФ
- 21. Матрично-векторная форма ДПФ
- 22. Определение обратного ДПФ
- 23. Фильтрация Фурье
- 24. Моделирование растений и графических объектов Случайные фракталы применяются для моделирования растений и разных графических объектов, например,
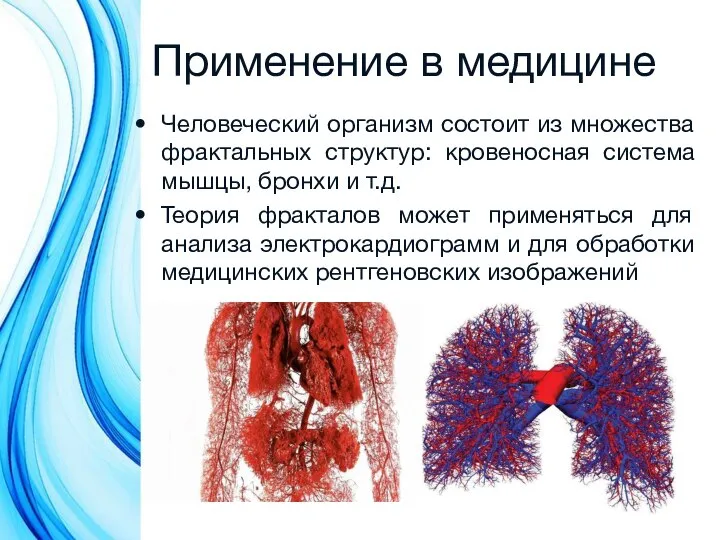
- 27. Применение в медицине Человеческий организм состоит из множества фрактальных структур: кровеносная система мышцы, бронхи и т.д.
- 28. Моделирование турбулентного движения Изучение турбулентности в потоках очень хорошо подстраивается под фракталы. Турбулентные потоки хаотичны и
- 31. Скачать презентацию
























 Презентация на тему Конвекция
Презентация на тему Конвекция  Однофазный синусоидальный ток
Однофазный синусоидальный ток Система охлаждения двигателя
Система охлаждения двигателя Давление газа
Давление газа Магнитные свойства вещества. Сила Лоренца
Магнитные свойства вещества. Сила Лоренца Исследование радиального профиля параметров активной среды лазеров с разрядом в полом катоде
Исследование радиального профиля параметров активной среды лазеров с разрядом в полом катоде 14 Лучистый теплообмен. Расчёт угловых коэффициентов. Казаков +
14 Лучистый теплообмен. Расчёт угловых коэффициентов. Казаков + Геометрическая оптика. Свет. Источники света
Геометрическая оптика. Свет. Источники света Проектирование компрессорных установок горных предприятий. Занятие 7
Проектирование компрессорных установок горных предприятий. Занятие 7 Источники света. Прямолинейное распространение света
Источники света. Прямолинейное распространение света Инерция
Инерция Учимся мыслить
Учимся мыслить Деление ядер урана
Деление ядер урана Генератор 2ГВ-008
Генератор 2ГВ-008 Движение и его относительность
Движение и его относительность Электричество. Простейшая электрическая цепь. Первая помощь при ударе электрическим током
Электричество. Простейшая электрическая цепь. Первая помощь при ударе электрическим током Радиоактивные превращения. Экспериментальные методы исследования частиц
Радиоактивные превращения. Экспериментальные методы исследования частиц Звездный час (викторина)
Звездный час (викторина) Презентация на тему Планетарная модель атома
Презентация на тему Планетарная модель атома  Поглощенная доза излучения. Основы дозиметрии
Поглощенная доза излучения. Основы дозиметрии Подготовка к ЕГЭ на уроках физики
Подготовка к ЕГЭ на уроках физики Динамика моря и Условия судоходства
Динамика моря и Условия судоходства Презентация на тему Колебательный контур
Презентация на тему Колебательный контур  Решение задач Закон сохранения энергии
Решение задач Закон сохранения энергии Испарение и конденсация
Испарение и конденсация Магнитное поле. Лекция 20
Магнитное поле. Лекция 20 Презентация на тему Построения в линзах
Презентация на тему Построения в линзах  Физика. Вводная лекция
Физика. Вводная лекция