Содержание
- 2. Циклирование фазы
- 3. Приёмник: (0, 270, 180, 90) Δp=-3: (0, 270, 180, 90) -> (+, +, +, +) Δp=-2:
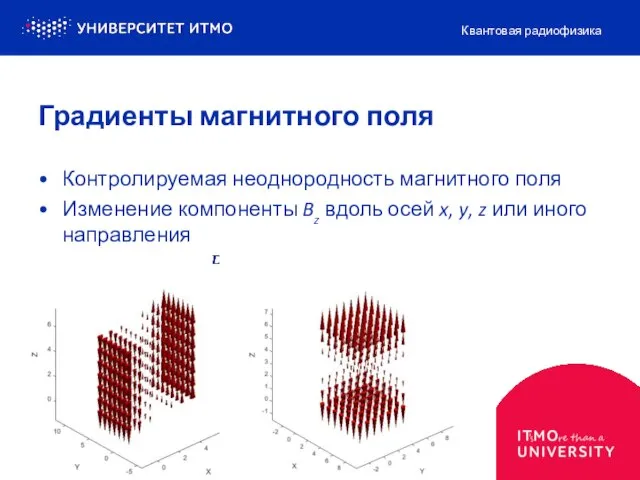
- 4. Пространственная чувствительность ЯМР-экспериментов
- 5. Контролируемая неоднородность магнитного поля Изменение компоненты Bz вдоль осей x, y, z или иного направления Квантовая
- 6. Во вращающейся системе координат, без учета релаксационных эффектов Квантовая радиофизика Уравнения Блоха в присутствии градиента магнитного
- 7. Решение уравнений для намагниченности с начальными значениями продольной и поперечной компонент µT(0) и µz(0) При сонаправленности
- 8. Сигнал (от всего образца) Спектр Квантовая радиофизика Спектр FID в присутствии градиента Bz
- 9. Сигнал (от всего образца) Спектр Квантовая радиофизика Спектр FID в присутствии градиента Bz
- 10. Квантовая радиофизика FID в присутствии градиента Bz
- 11. Чувствительность ЯМР-экспериментов к движению
- 12. x=x(t) Рассмотрим разложение x(t) в ряд Квантовая радиофизика Движение частиц при воздействии градиента
- 13. Фазовые члены в выражении для намагниченности Можно подобрать форму G=G(t) таким образом, чтобы выполнялось одно или
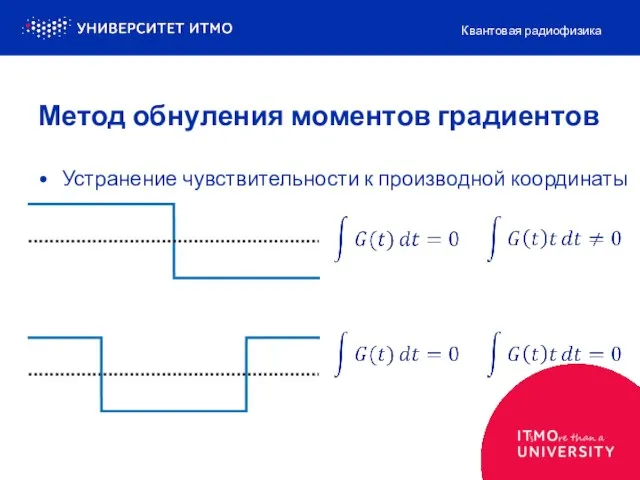
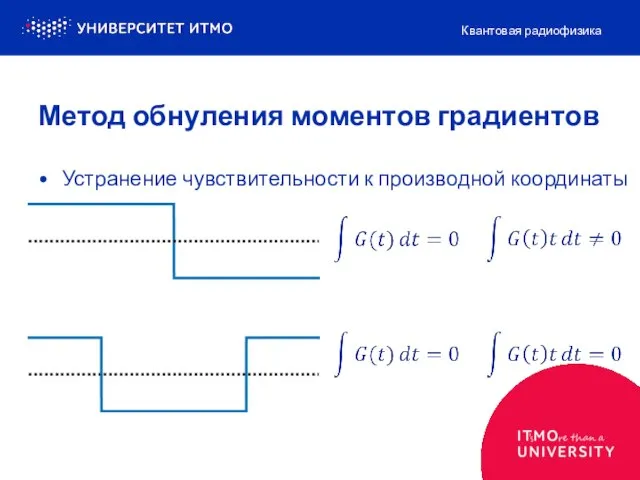
- 14. Устранение чувствительности к производной координаты Квантовая радиофизика Метод обнуления моментов градиентов
- 15. Устранение чувствительности к производной координаты Квантовая радиофизика Метод обнуления моментов градиентов
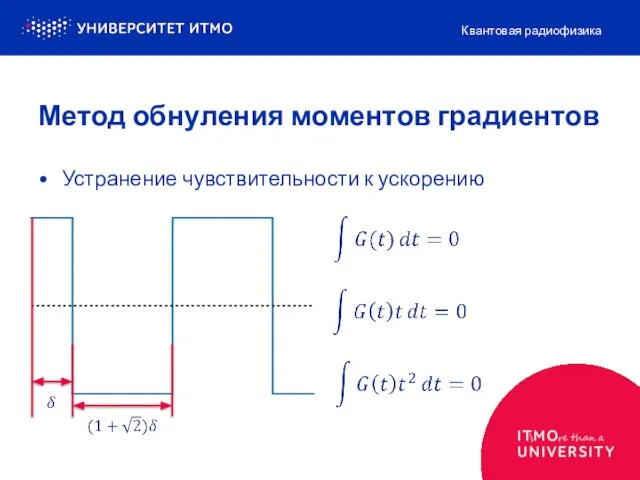
- 16. Устранение чувствительности к ускорению Квантовая радиофизика Метод обнуления моментов градиентов
- 17. Используется последовательность с импульсным градиентом с нулевым первым моментом Предполагается ламинарный поток Квантовая радиофизика Измерение скорости
- 18. Выражение для сигнала ЯМР Два эксперимента с импульсами градиента разной полярности (вариант +G/-G или +G/0) Точность
- 20. Скачать презентацию













 Ядерные силы. Ядерные реакции
Ядерные силы. Ядерные реакции Коробка передач
Коробка передач Experimental studies of modular generator
Experimental studies of modular generator Радиактивность
Радиактивность Холлофайбер – универсальный теплоизоляционный материал нового века
Холлофайбер – универсальный теплоизоляционный материал нового века Лекция 1
Лекция 1 Определение параметров колебательного движения
Определение параметров колебательного движения Измерение физических величин
Измерение физических величин Презентация на тему Расчёт массы тела по его плотности
Презентация на тему Расчёт массы тела по его плотности 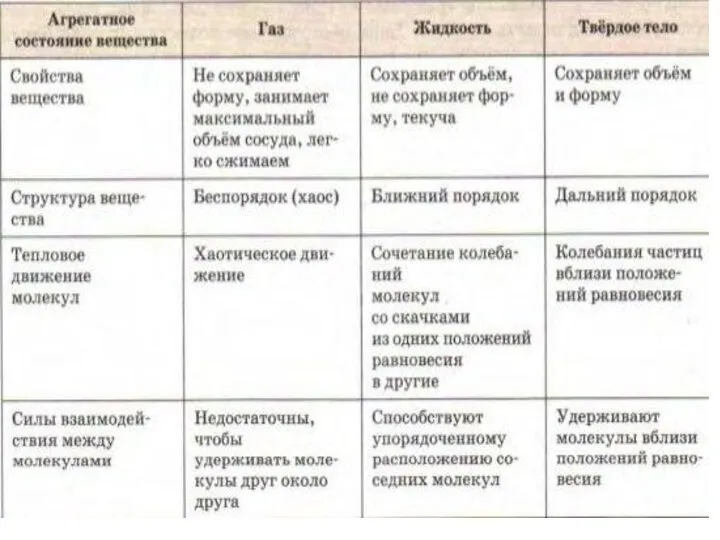 Свойства жидкостей
Свойства жидкостей Адронный коллайдер
Адронный коллайдер Динамика вращательного движения
Динамика вращательного движения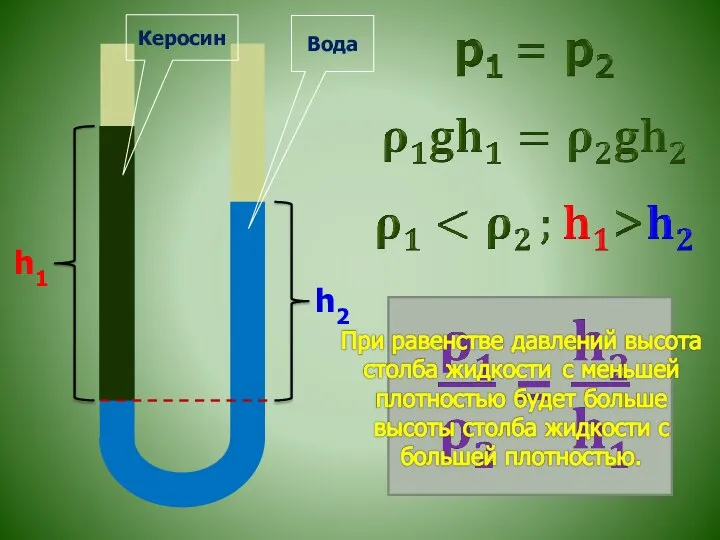 Шлюзы и фонтаны
Шлюзы и фонтаны Задачи небесной механики
Задачи небесной механики Исследование зависимости угла преломления от угла падения света
Исследование зависимости угла преломления от угла падения света Идеальный газ
Идеальный газ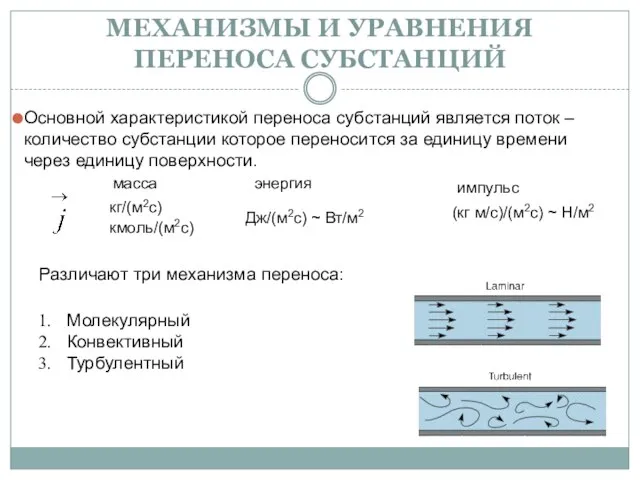 Механизмы и уравнения переноса субстанций
Механизмы и уравнения переноса субстанций Применение ядерной энергии в различных отраслях. Доза радиоактивного излучения
Применение ядерной энергии в различных отраслях. Доза радиоактивного излучения Порівняння роботи рухомого складу за різними видами тяги
Порівняння роботи рухомого складу за різними видами тяги Постоянный_электрический_ток
Постоянный_электрический_ток Коэффициент отражения
Коэффициент отражения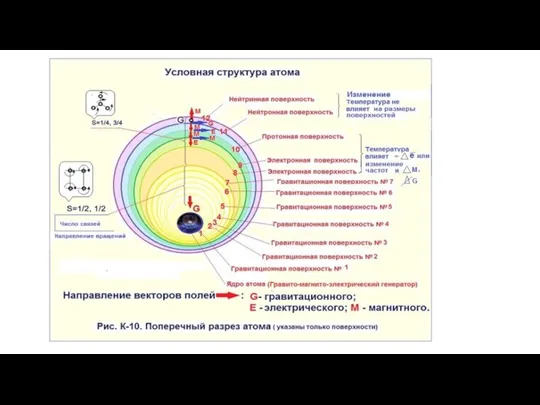 Условная структура атома
Условная структура атома Лампа накаливания. История создания. Современная конструкция
Лампа накаливания. История создания. Современная конструкция Izolace, separace a detekce proteinů část ii
Izolace, separace a detekce proteinů část ii Деление атомного ядра
Деление атомного ядра Эпиграфы
Эпиграфы Механические передачи. Цилиндрические и конические зубчатые передачи. (Лекция 5)
Механические передачи. Цилиндрические и конические зубчатые передачи. (Лекция 5) Аккумулирование энергии
Аккумулирование энергии