Гидродинамика

Расчёт простых трубопроводных систем
При расчёте простых трубопроводов в зависимости от поставленной задачи, известных и определяемых параметров выделяют три типа расчётов.
1 Определение напора (Н) или давления (р) при известных: расходе жидкости (Q), геометрических размерах трубопровода (длине l, диаметре d), местных сопротивлениях на трубопроводе.
2 Определение расхода (Q), или пропускной способности трубопровода, при известных: действующем напоре (H) или давлении (р) в системе; геометрических размерах и установленных местных сопротивлениях.

3 Определение геометрических размеров трубопроводов (l; d), характеристик местных сопротивлений при известном расходе (Q), действующем напоре (Н) или давлении (р). Наиболее трудоёмкой считается задача по определению диаметра (d) трубопровода, так как такой расчёт проводится методом подбора и пересчёта нескольких вариантов.
Рассмотрим расчёт простого трубопровода. Здесь возможны два случая: истечение жидкости в атмосферу и истечение подуровень.
Расчёты простых трубопроводных систем основаны на использовании основного уравнения гидродинамики - уравнения Бернулли.

Расчёт простой трубопроводной системы с истечением жидкости в атмосферу
На рисунке представлена схема простого водопровода с водонапорной башней, создающей постоянный напор Н. Известны длина трубопровода l, диаметр d, местные сопротивления в виде входа в трубу, вентиля и двух колен (отводов).
Давление на поверхности воды в баке атмосферное (рa), выход воды в конце трубы также в атмосферу (ра)

В представленной схеме действующий напор H считается постоянным, уровень жидкости в напорном баке поддерживается на постоянном горизонте за счёт подачи воды (или другой жидкости) в бак, например, из скважины или от насосной установки, так, чтобы автоматически регулировался приток в бак, равным расходу жидкости в системе. Постоянная подача жидкости показана по трубопроводу, обозначенному пунктирной линией.

В дальнейших схемах трубопроводных систем приток жидкости в систему не обозначается, но всегда подразумевается установившееся движение, т. е. скорость движения жидкости в трубе не изменяется во времени.
Расчёт простой системы проведём путём применения уравнения Бернулли.
Согласно методике составления уравнения, выполним следующие пункты.
1 Выбираем два сечения: одно сечение проводим по свободной поверхности в напорном баке (башне), где скорость допустимо считать равной нулю (уровень жидкости постоянный, движения нет), другое - на выходе жидкости из трубы, где существует определённая скорость движения.
2 Сечения 1-1 и 2-2 нумеруем по направлению движения жидкости.
3 В выбранных сечениях учитываем абсолютное давление, т. е. давление, рассчитанное с учётом атмосферного: р1 =рa, р2 =рa.

4 Плоскость сравнения 0-0 совместим с сечением 2-2, тогда z1 = Н; z2 = 0. Если бы плоскость сравнения совместили с сечением 1-1, тогда z1 = 0; z2 = - H. Помним, что отсчёты от плоскости сравнения вверх считаются положительными, вниз - отрицательными.
Записываем уравнение Бернулли в общем виде и расписываем значение всех параметров:
z1 = H; z2 = 0
р1=ра р2=ра
v1=0 α2 = 1,0; v2=v;
для коэффициента α2 предполагаем турбулентный режим в круглой трубе.

Расчёт простой трубопроводной системы при истечении жидкости под уровень
Истечением подуровень считается случай, когда жидкость поступает в резервуар, заполненный жидкостью, т. е. под уровень жидкости. Схема трубопровода с истечением под уровень представлена на рисунке, но выход жидкости направлен в другой открытый резервуар.
Для расчёта простой системы с истечением под уровень воспользуемся также уравнением Бернулли:
1 Выберем два сечения по свободным поверхностям жидкости в резервуарах, где скорости жидкости равны нулю.

2 Сечения 1-1 и 2-2 пронумеруем по направлению движения жидкости.
3 Учтём абсолютные давления в выбранных сечениях: р1 = ра; р2 = ра
4 Плоскость сравнения 0-0 совместим с сечением 2-2, тогда z1 = Н;
z2 = 0.
5 Запишем уравнение Бернулли в общем виде и покажем подстановку параметров:
z1 = H; z2 = 0
р1=ра р2=ра
v1=0 v2=0;

Если режим движения и зона сопротивления не подтвердится, проводится повторный расчёт коэффициента λ в соответствии с числом Re по схеме.
После окончательного уточнения режима движения и области сопротивления определяется коэффициент λ и рассчитывается расход Q.
Как правило, при движении воды в шероховатых трубах имеет место турбулентный режим, зона квадратичного сопротивления.
Расчёт простых систем третьего типа по определению длины или значений коэффициентов местных сопротивлений различных устройств (кранов, задвижек, диафрагм и им подобных) не представляет трудности.
Составляется уравнение Бернулли для характерных сечений, затем оно преобразуется в буквенное выражение для расчёта предельной длины трубопровода или для определения коэффициента местного сопротивления какого-либо устройства. В буквенное выражение подставляется значение заданных или рассчитанных параметров.

На практике для расчёта диаметра трубопровода пользуются оптимальными значениями скоростей: при движении в водопроводных системах скорость v = (0,8 - 1,2) м/с, реже до 1,5 м/с; для шахтных водоотливных трубопроводов v - (2,0 - 2,5) м/с.
Следует отметить, что для технико-экономических расчётов по определению оптимальных значений диаметров трубопроводов следует пользоваться специальной литературой и таблицами.

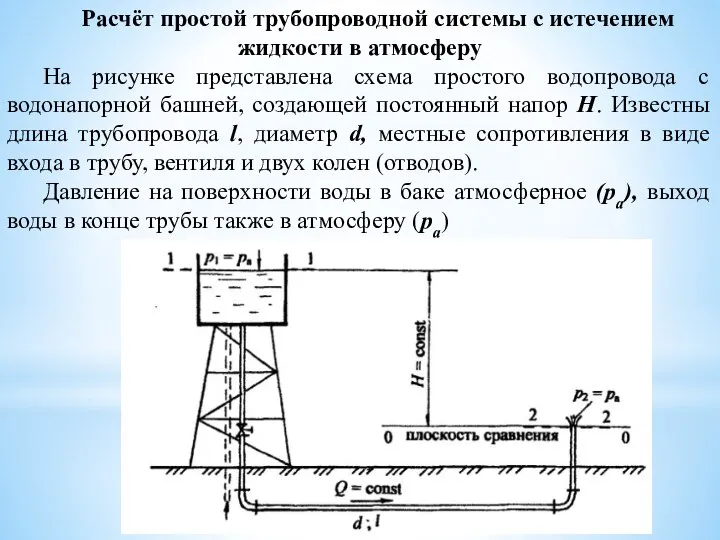
Пример 1. С помощью насоса по трубе диаметром d = 50 мм и длиной l = 70 м нефть подаётся в закрытый резервуар на высоту Н = 15 м. Считать Н = const.
Определить показание мановакуумметра (рмв), установленного на поверхности нефти в закрытом резервуаре, если показание манометра после насоса рман = 1,3 ат. Расход нефти Q = 1,2 л/с, плотность нефти ?н = 900 кг/м3, относительная вязкость по Энглеру °Е = 4,0. В системе установлен пробковый кран с углом закрытия α = 400 и два колена с коэффициентом сопротивления ζкол= 0,8.
Решение. Представленная трубопроводная система относится к первому типу простых систем.
Следует вспомнить, что мановакуумметр - это прибор, который может измерять, как манометрическое (избыточное) давление, так и вакуум. При решении задачи давление на поверхности нефти будем обозначать рма.
Если при решении задачи значение давления получится положительным, значит, мановакуумметр работает, как манометр; отрицательное значение давления означает, что мановакуумметр работает, как вакуумметр.

Для определения показания мановакуумметра воспользуемся уравнением Бернулли. Согласно методике составления уравнения:
1 Выбираем два сечения: одно - в месте установки манометра, это сечение проводим нормально к направлению движения жидкости, где скорость равна скорости движения нефти в трубе - v; другое - по свободной поверхности в резервуаре, где давление определяется по мановакуумметру, а скорость равна нулю.
2 Сечения 1-1 и 2-2 нумеруем по направлению движения жидкости, чтобы в уравнении потери напора в гидравлических сопротивлениях учитывались со знаком "+".
3 В выбранных сечениях принимаем абсолютное давление, т. е. с учётом атмосферного: р1 = ра + рман р2 = ра + рма

Рассчитаем все слагаемые в уравнении :

Пример 2. Вода из закрытого резервуара А поступает в открытый резервуар В при пропускной способности системы Q = 15 л/с по трубам: d1 = 75 мм; l1 = 8 м и l2 = 12 м; d2 =100 мм и l3 = 15 м. Напоры воды в резервуарах постоянны относительно оси трубы: Н1 = 1,5 м; Н2 = 3,5 м.
Определить показание манометра (рман) на поверхности воды в закрытом резервуаре, а также соответствующий манометрический напор (Нман).
Принять абсолютную шероховатость труб: ∆1 =0,5 мм; ∆2 = 0,2 мм. Учесть местные сопротивления в системе: на входе в первую трубу; в пробковом кране при угле закрытия α = 300; при внезапном расширении и на выходе из второй трубы.
Движение воды в системе считать установившемся, т.е. Q = const. Построить линию полного напора (напорную линию), пьезометрическую линию, показать эпюру потерь напора.

Решение. Представленная схема относится к простым трубопроводным системам первого типа с истечением подуровень.
Для определения избыточного (манометрического) давления (рман) на поверхности воды в резервуаре А воспользуемся уравнением Бернулли:
1 Выберем два сечения по свободным поверхностям в резервуарах, где скорость допустимо считать равной нулю.
2 Сечения 1-1 и 2-2 пронумеруем по направлению движения воды.
3 В выбранных сечениях учтём абсолютное давление: р1 = ра + рман; р2= ра
4 Плоскость сравнения совместим с осью трубы, тогда z1 = H1 ; z2 = H2 .
5 Запишем уравнение Бернулли в общем виде и решим его:
после подстановки параметров и сокращении получим: