Векторное произведение

Определение векторного произведения
Система координат — способ определить положение и перемещение точки или тела с помощью чисел или других символов.
Координаты — это совокупность чисел, которые определяют положение какого-либо объекта на прямой, плоскости, поверхности или в пространстве. Как найти координаты точки мы рассказали в этой статье.
Скаляр — это величина, которая полностью определяется в любой координатной системе одним числом или функцией.
Вектор — направленный отрезок прямой, для которого указано, какая точка является началом, а какая — концом.
Вектор с началом в точке A и концом в точке B принято обозначать как →AB. Векторы также можно обозначать малыми латинскими буквами со стрелкой или черточкой над ними, вот так: →a.
Коллинеарность — отношение параллельности векторов. Два ненулевых вектора называются коллинеарными, если они лежат на параллельных прямых или на одной прямой.
Проще говоря это «параллельные» векторы. Коллинеарные векторы могут быть одинаково направлены или противоположно направлены.

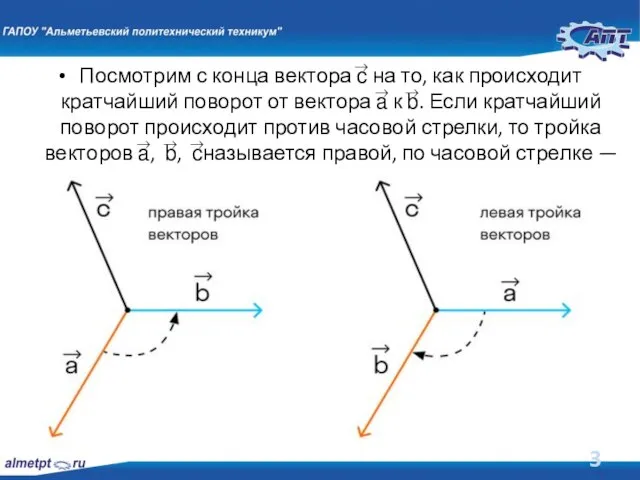
Посмотрим с конца вектора с⃗ на то, как происходит кратчайший поворот от вектора a⃗ к b⃗. Если кратчайший поворот происходит против часовой стрелки, то тройка векторов а⃗, b⃗, c⃗называется правой, по часовой стрелке — левой.

Векторным произведением двух векторов a ⃗ и b ⃗, которые заданы в прямоугольной системе координат трехмерного пространства, называется такой вектор с ⃗, что:
он является нулевым, если векторы a ⃗ и b ⃗ коллинеарные;
он перпендикулярен и вектору a ⃗ и вектору b ⃗;
длина векторного произведения равна произведению длин векторов a ⃗ и b ⃗ на синус угла между ними
тройка векторов a ⃗, b ⃗ , c ⃗ ориентирована так же, как и заданная система координат.

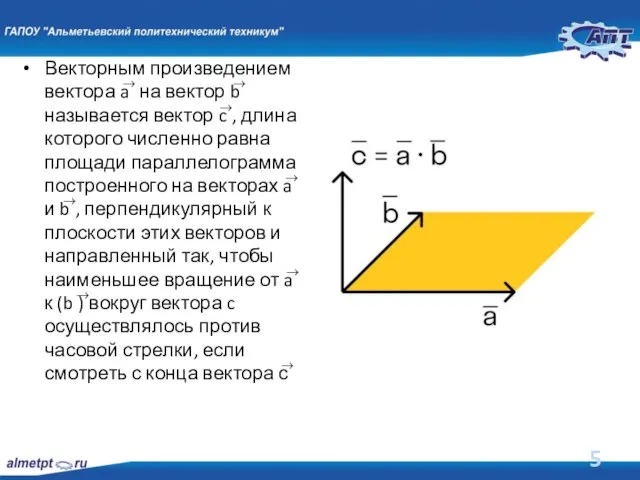
Векторным произведением вектора a ⃗ на вектор b ⃗ называется вектор c ⃗, длина которого численно равна площади параллелограмма построенного на векторах a ⃗ и b ⃗, перпендикулярный к плоскости этих векторов и направленный так, чтобы наименьшее вращение от a ⃗ к (b ) ⃗вокруг вектора c осуществлялось против часовой стрелки, если смотреть с конца вектора с ⃗

Векторное произведение двух векторов a = {ax; ay; az} и b = {bx; by; bz} в декартовой системе координат — это вектор, значение которого можно вычислить, используя формулы вычисления векторного произведения векторов:

Координаты векторного произведения
Рассмотрим векторное произведение векторов в координатах.
Сформулируем второе определение векторного произведения, которое позволяет находить его координаты по координатам заданных векторов.
В прямоугольной системе координат трехмерного пространства векторное произведение двух векторов a ⃗= (ax, ay, az) и b ⃗= (bx, by, bz) есть вектор
где i ⃗, j ⃗, k ⃗,— координатные векторы.
Это определение показывает нам векторное произведение в координатной форме.
Векторное произведение удобно представлять в виде определителя квадратной матрицы третьего порядка, первая строка которой есть орты i ⃗, j ⃗, k ⃗, во второй строке находятся координаты вектора a ⃗, а в третьей — координаты вектора b ⃗ в заданной прямоугольной системе координат:

Если разложим этот определитель по элементам первой строки, то получим равенство из определения векторного произведения в координатах:

Свойства векторного произведения
Векторное произведение в координатах представляется в виде определителя матрицы:
На основании свойств определителя можно легко обосновать свойства векторного произведения векторов: 3. Сочетательное свойство
1. Антикоммутативность
2.Свойство дистрибутивности