Содержание
- 2. Предмет молекулярной физики. Статистический и термодинамический методы исследований. Молекулярно-кинетическая теория идеального газа. Уравнение состояния. Законы: Авогадро,
- 3. Молекулярно-кинетическая теория (МКТ) исходит из молекулярно-кинетических представлений: 1) все вещества состоят из молекул (атомов); 2) молекулы
- 4. метод основан на том, что свойства макросистем, состоящих из большого числа микрочастиц, определяются усреднёнными значениями характеристик
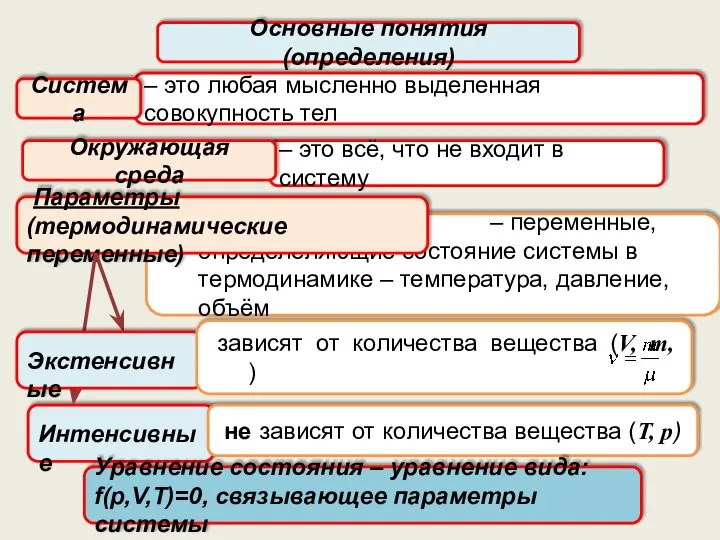
- 5. – это любая мысленно выделенная совокупность тел Основные понятия (определения) Система – это всё, что не
- 6. При нормальных условиях ( T=273 К, p= 105 Па) газ можно считать идеальным Молекулярно-кинетическая теория идеального
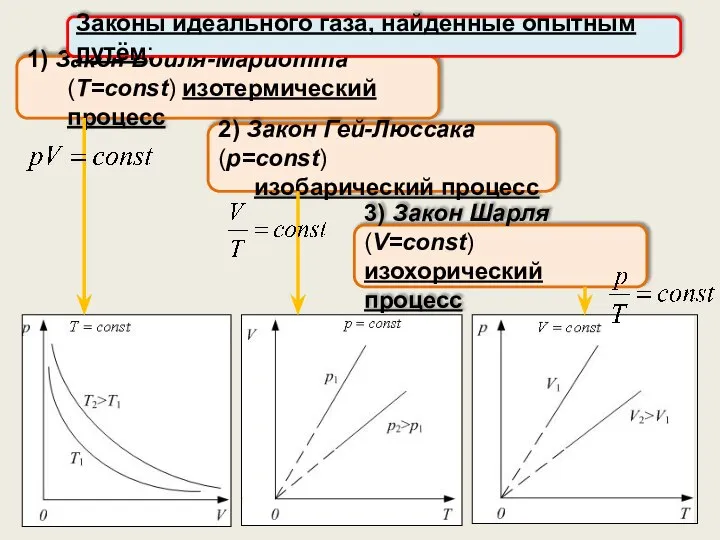
- 7. 1) Закон Бойля-Мариотта (T=const) изотермический процесс Законы идеального газа, найденные опытным путём: 2) Закон Гей-Люссака (p=const)
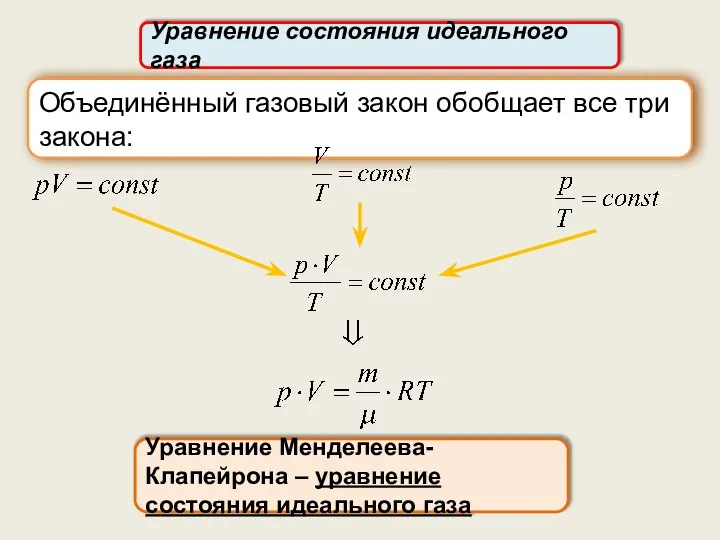
- 8. Уравнение состояния идеального газа Уравнение Менделеева-Клапейрона – уравнение состояния идеального газа Объединённый газовый закон обобщает все
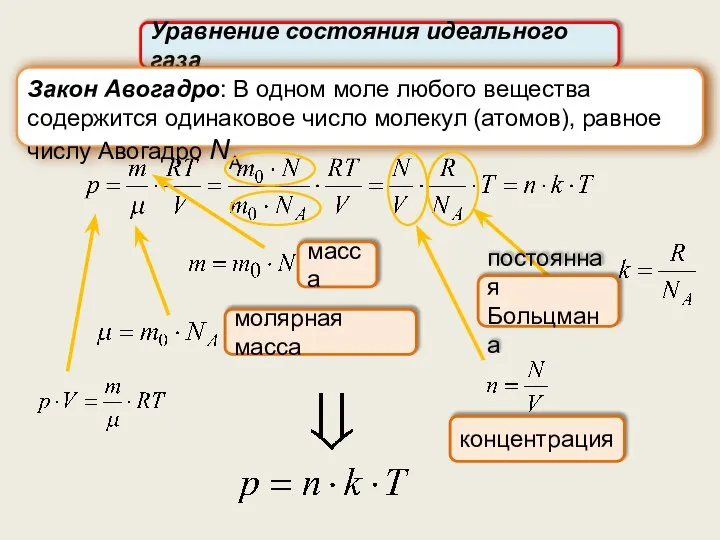
- 9. Уравнение состояния идеального газа молярная масса Закон Авогадро: В одном моле любого вещества содержится одинаковое число
- 10. Давление смеси газов Доказательство: Закон Дальтона: давление смеси газов равно сумме парциальных давлений всех входящих в
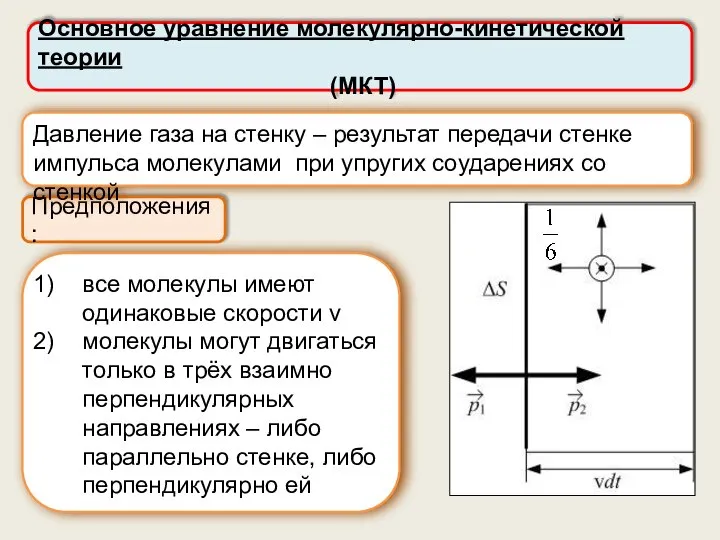
- 11. Основное уравнение молекулярно-кинетической теории (МКТ) Предположения: Давление газа на стенку – результат передачи стенке импульса молекулами
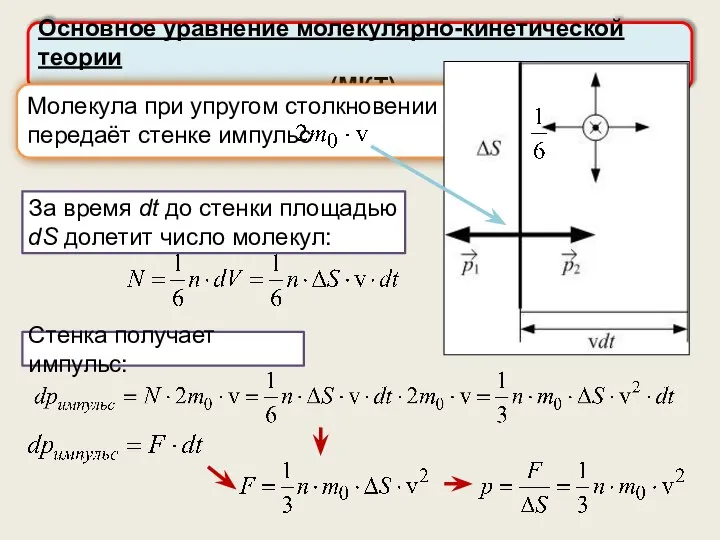
- 12. Основное уравнение молекулярно-кинетической теории (МКТ) Молекула при упругом столкновении передаёт стенке импульс За время dt до
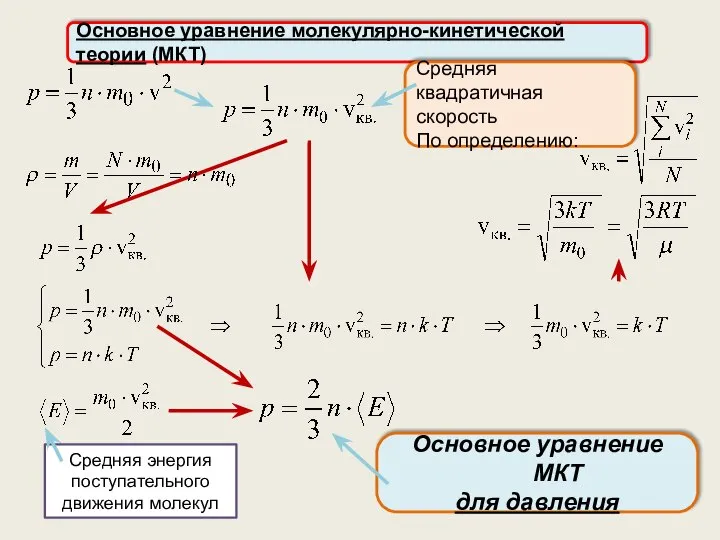
- 13. Основное уравнение молекулярно-кинетической теории (МКТ) Средняя квадратичная скорость По определению: Основное уравнение МКТ для давления Средняя
- 14. Основное уравнение молекулярно-кинетической теории (МКТ) Отсюда смысл абсолютной температуры: при абсолютном нуле (T=0 К) прекращается тепловое
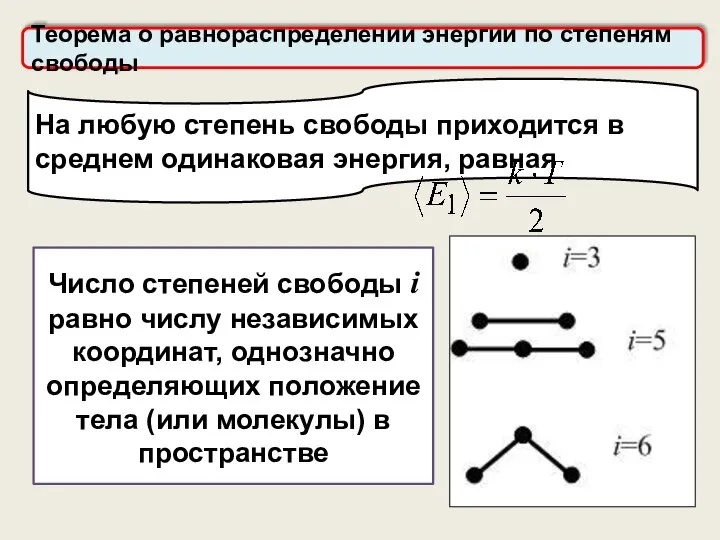
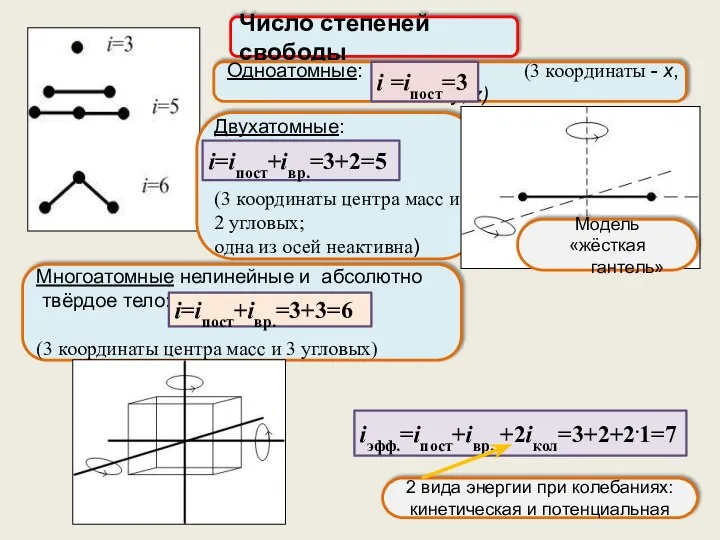
- 15. Число степеней свободы i равно числу независимых координат, однозначно определяющих положение тела (или молекулы) в пространстве
- 16. Число степеней свободы Одноатомные: (3 координаты - x, y, z) i =iпост=3 Двухатомные: (3 координаты центра
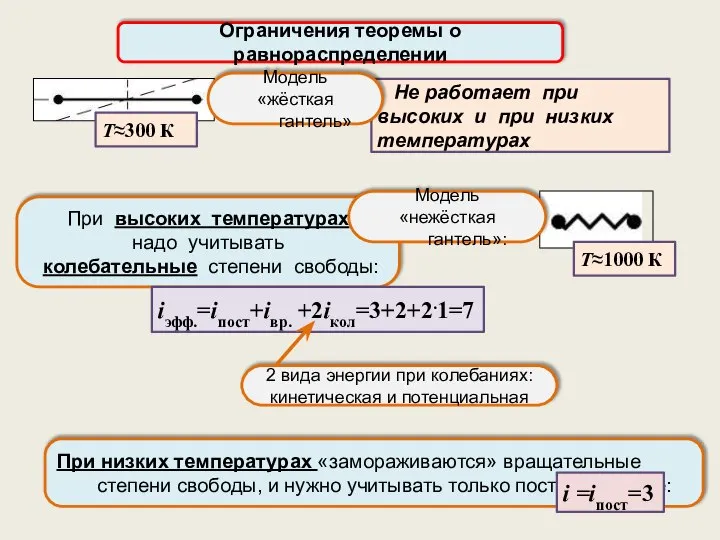
- 17. При высоких температурах надо учитывать колебательные степени свободы: При низких температурах «замораживаются» вращательные степени свободы, и
- 18. Внутренняя энергия идеального газа – суммарная кинетическая энергия всех молекул; потенциальная энергия взаимодействия молекул не учитывается
- 19. Термодинамика изучает общие свойства макросистем, находящихся в состоянии термодинамического равновесия, и процессы перехода между состояниями. Термодинамика
- 20. Предмет и задачи термодинамики В механике переменными являются координаты и импульсы (скорости) частиц. В термодинамике такое
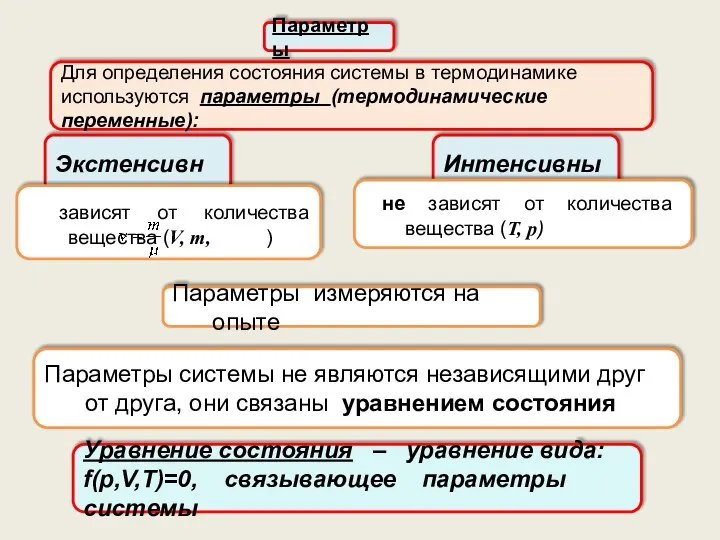
- 21. Параметры Для определения состояния системы в термодинамике используются параметры (термодинамические переменные): Экстенсивные Интенсивные зависят от количества
- 22. В термодинамике нет моделей, теоретических предположений о строении вещества или о механизме процессов. Свойства вещества –
- 23. Внутренняя энергия Внутренняя энергия системы – это функция состояния, то есть однозначно определяется состоянием системы. Изменение
- 24. Первое начало термодинамики Количество теплоты, сообщённое системе, идёт на приращение её внутренней энергии и на работу
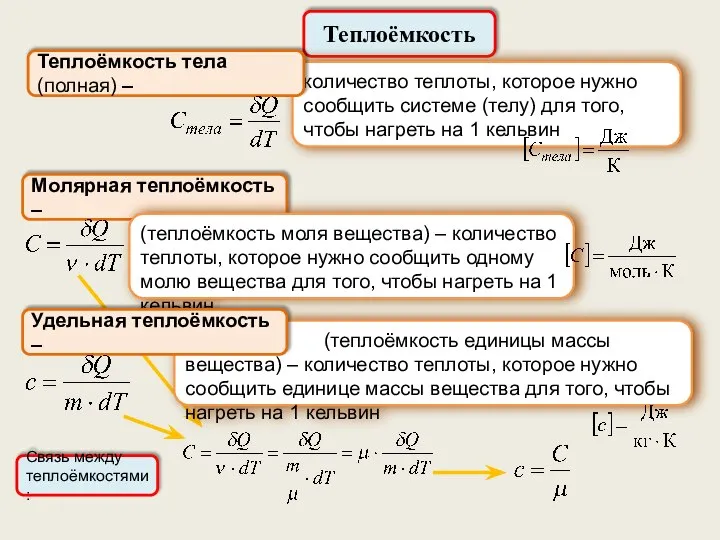
- 25. Теплоёмкость Молярная теплоёмкость – количество теплоты, которое нужно сообщить системе (телу) для того, чтобы нагреть на
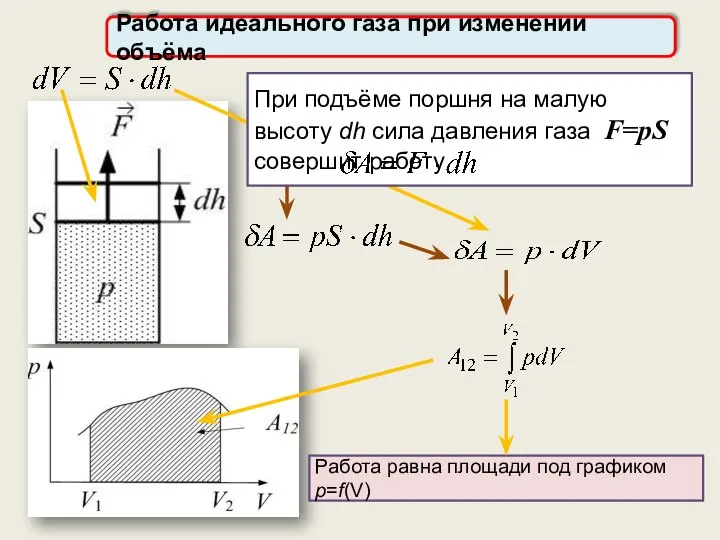
- 26. Работа идеального газа при изменении объёма При подъёме поршня на малую высоту dh сила давления газа
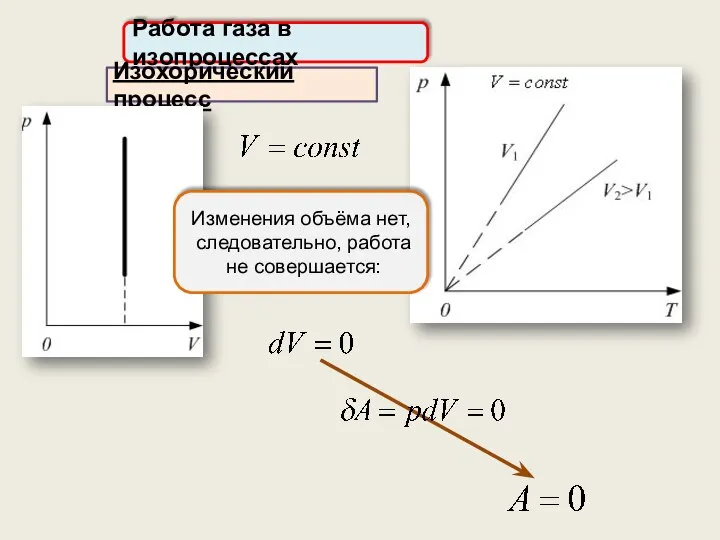
- 27. Работа газа в изопроцессах Изохорический процесс Изменения объёма нет, следовательно, работа не совершается:
- 28. Работа газа в изопроцессах Изобарический процесс Универсальная газовая постоянная R численно равна работе одного моля идеального
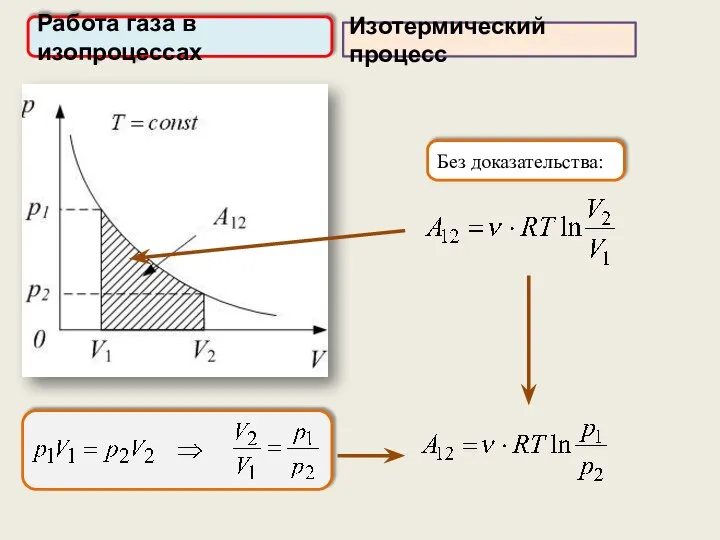
- 29. Работа газа в изопроцессах Изотермический процесс Без доказательства:
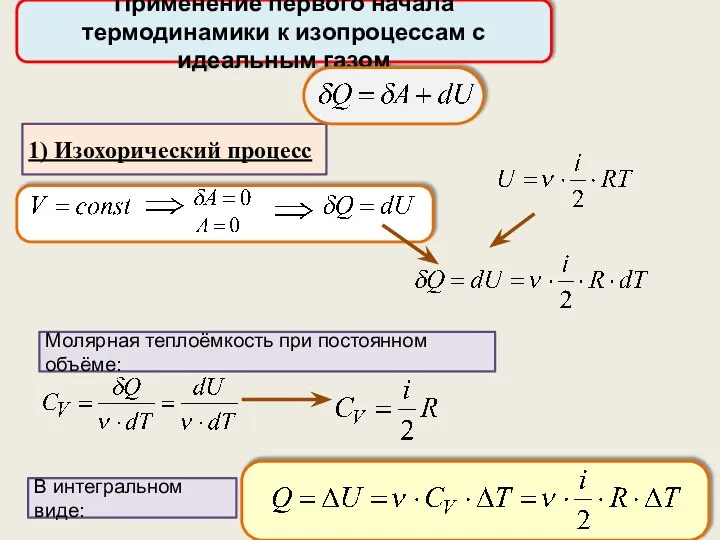
- 30. Применение первого начала термодинамики к изопроцессам с идеальным газом Молярная теплоёмкость при постоянном объёме: 1) Изохорический
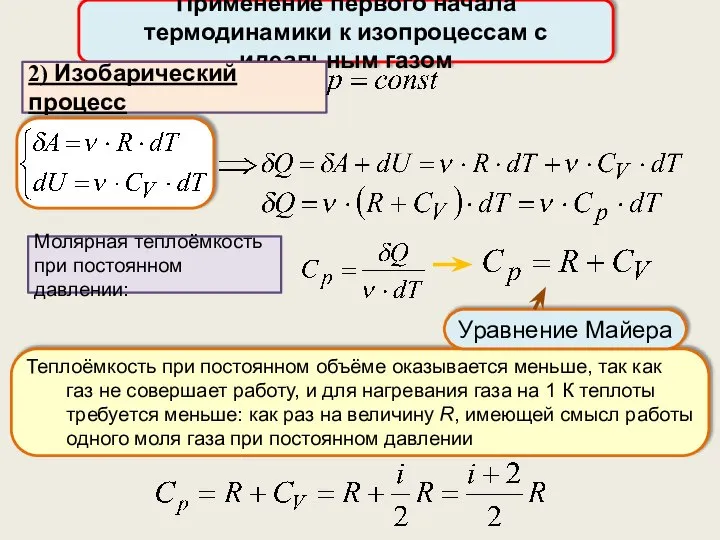
- 31. Применение первого начала термодинамики к изопроцессам с идеальным газом Молярная теплоёмкость при постоянном давлении: 2) Изобарический
- 32. Применение первого начала термодинамики к изопроцессам с идеальным газом 3) Изотермический процесс
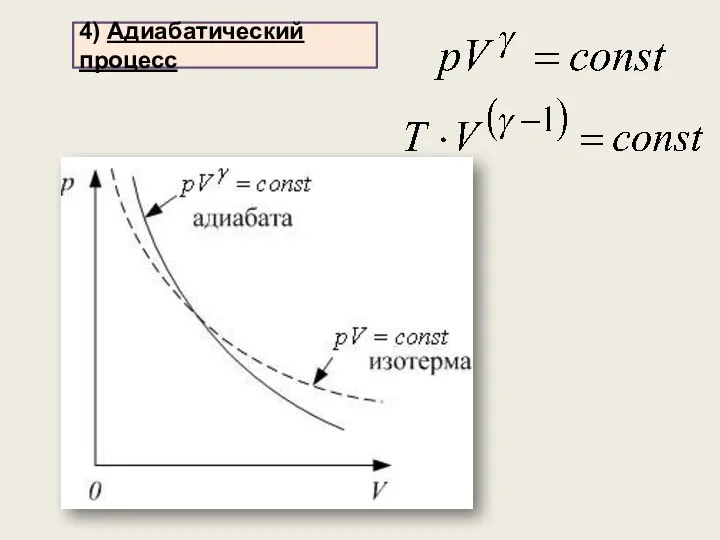
- 33. протекает без теплообмена с окружающей средой: система не получает и не отдаёт теплоты 4) Адиабатический процесс
- 34. 4) Адиабатический процесс
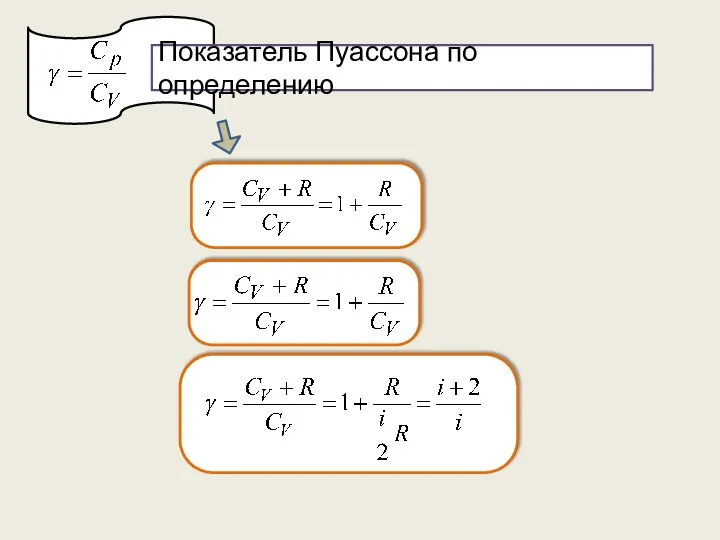
- 35. Показатель Пуассона по определению
- 36. Работа в адиабатическом процессе По первому началу термодинамики:
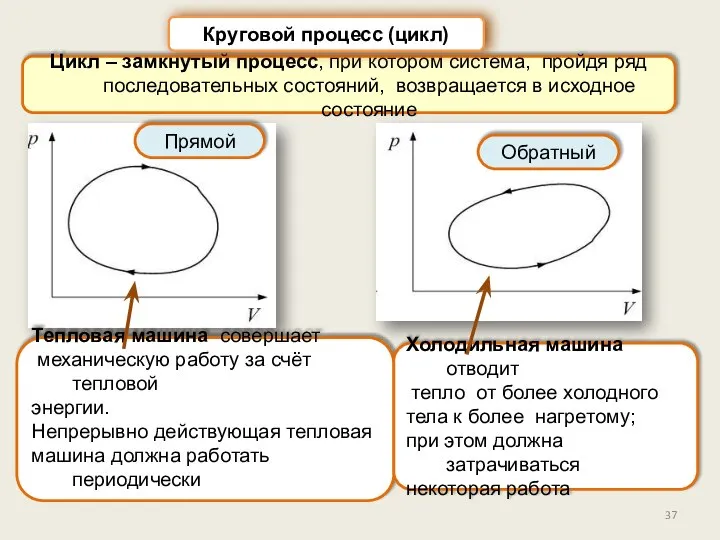
- 37. Цикл – замкнутый процесс, при котором система, пройдя ряд последовательных состояний, возвращается в исходное состояние Круговой
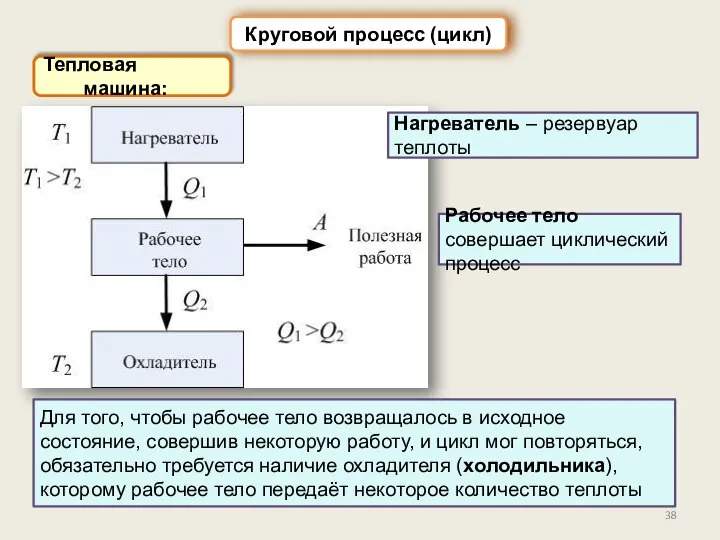
- 38. Тепловая машина: Круговой процесс (цикл) Рабочее тело совершает циклический процесс Нагреватель – резервуар теплоты Для того,
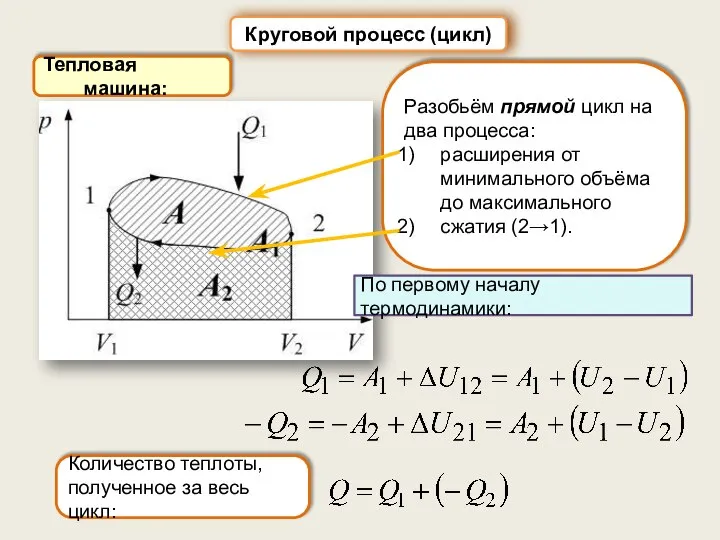
- 39. Тепловая машина: Круговой процесс (цикл) Разобьём прямой цикл на два процесса: расширения от минимального объёма до
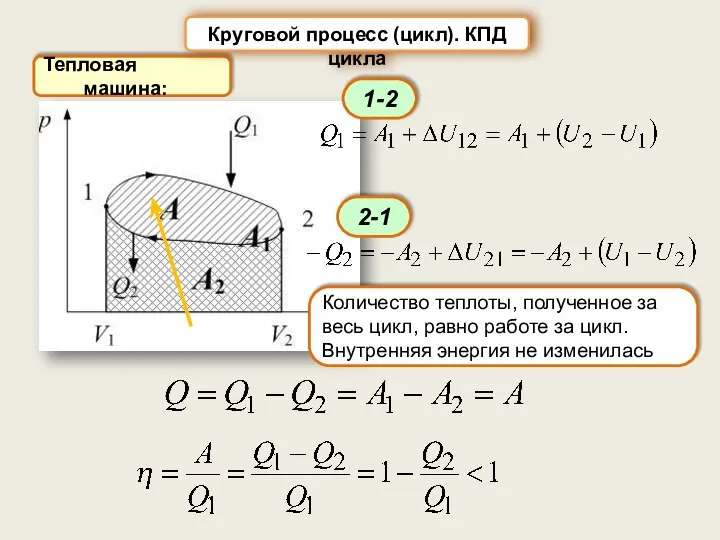
- 40. Тепловая машина: Круговой процесс (цикл). КПД цикла Количество теплоты, полученное за весь цикл, равно работе за
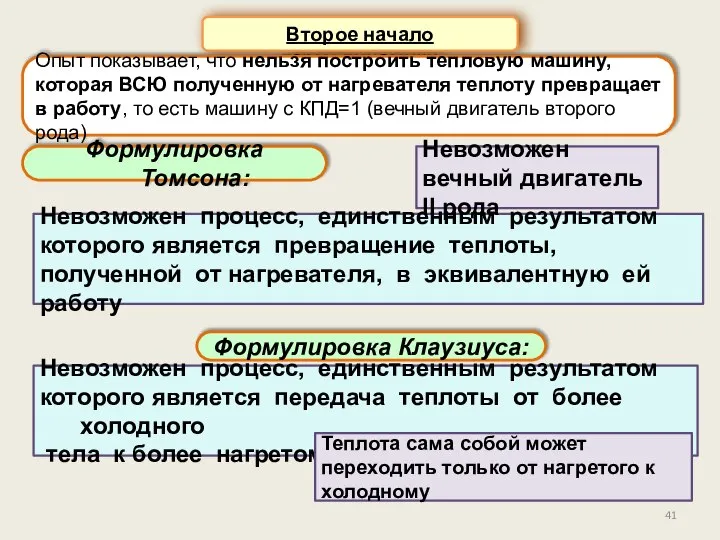
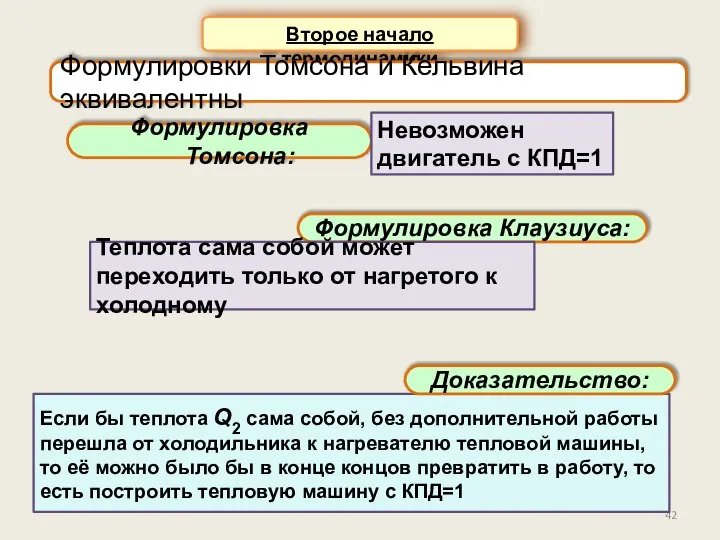
- 41. Второе начало термодинамики Формулировка Томсона: Опыт показывает, что нельзя построить тепловую машину, которая ВСЮ полученную от
- 42. Второе начало термодинамики Формулировка Томсона: Формулировки Томсона и Кельвина эквивалентны Если бы теплота Q2 сама собой,
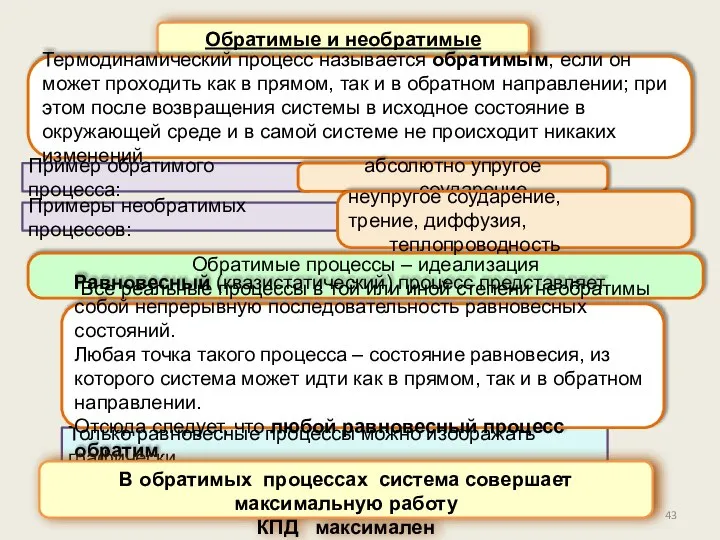
- 43. Обратимые и необратимые процессы Термодинамический процесс называется обратимым, если он может проходить как в прямом, так
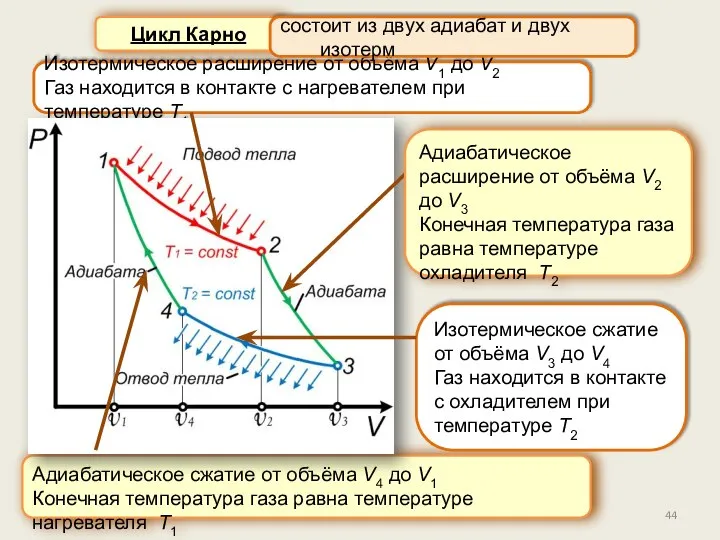
- 44. Цикл Карно Изотермическое расширение от объёма V1 до V2 Газ находится в контакте с нагревателем при
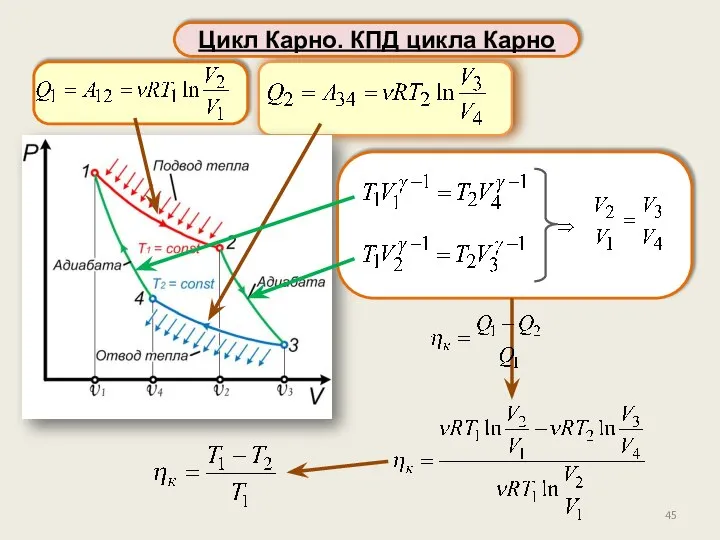
- 45. Цикл Карно. КПД цикла Карно
- 46. Теорема Карно 1) КПД цикла Карно не зависит от природы рабочего тела и определяется только температурами
- 48. Скачать презентацию

















 Исследование деформаций в тонкостенной цилиндрической оболочке
Исследование деформаций в тонкостенной цилиндрической оболочке Развитие взглядов на строение вещества
Развитие взглядов на строение вещества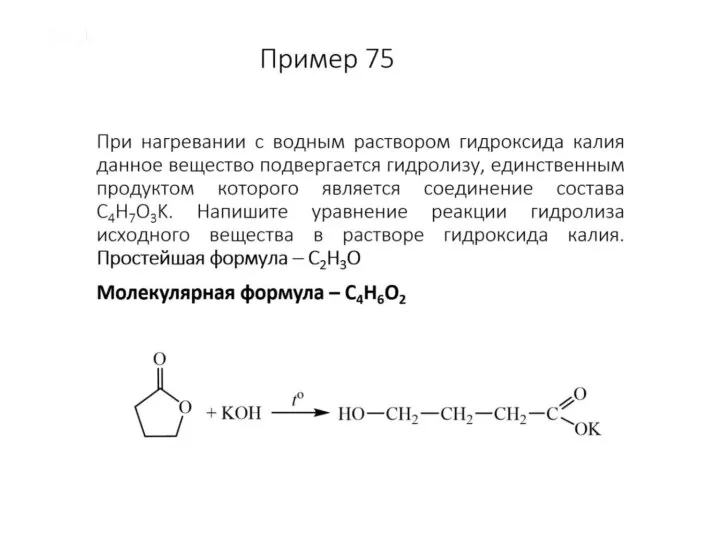 Задачи по физике
Задачи по физике Теплоносители и их свойства. Местная вентиляция и кондиционирование воздуха. (Тема 14)
Теплоносители и их свойства. Местная вентиляция и кондиционирование воздуха. (Тема 14) Тюнинг - стайлинг
Тюнинг - стайлинг Перепад давления
Перепад давления Закон Ома. Сопротивление цепи
Закон Ома. Сопротивление цепи Измерение массы медицинского шприца (без иглы)
Измерение массы медицинского шприца (без иглы) Технічна механіка. Розрахунково-графічна робота С1
Технічна механіка. Розрахунково-графічна робота С1 Давление света
Давление света Концепции современного естествознания
Концепции современного естествознания Общие сведения о системах радиосвязи. Электропитание средств связи
Общие сведения о системах радиосвязи. Электропитание средств связи Методы исследования в биомеханике
Методы исследования в биомеханике Ошибки при синхронииации. Beamforming. Перераспределение частот
Ошибки при синхронииации. Beamforming. Перераспределение частот zamena_t_kolodok
zamena_t_kolodok Приспособления малой механизации
Приспособления малой механизации Курсовая работа. Расчет свободной энергии ферромагнетика методом гиббса
Курсовая работа. Расчет свободной энергии ферромагнетика методом гиббса Равнодействующая всех сил
Равнодействующая всех сил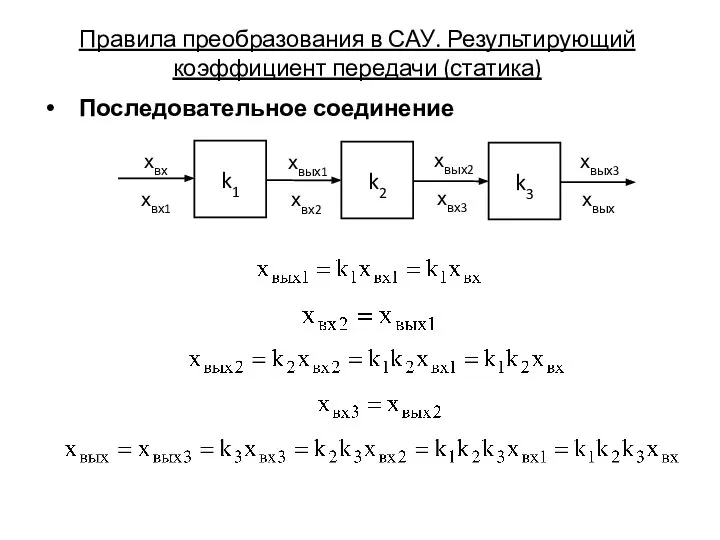 Правила преобразования в САУ. Результирующий коэффициент передачи (статика)
Правила преобразования в САУ. Результирующий коэффициент передачи (статика) Механические колебания
Механические колебания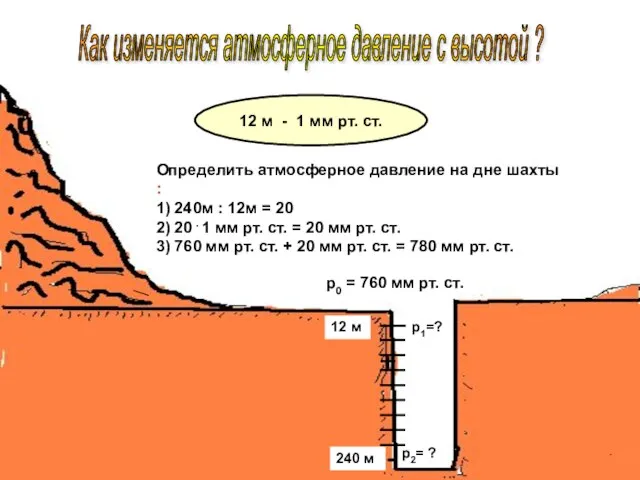 Презентация по физике "Как изменяется атмосферное давление с высотой ?" -
Презентация по физике "Как изменяется атмосферное давление с высотой ?" -  Реактивное движение
Реактивное движение 16M33┐є┐и▓ё╙═╗·┐к╖в┼р╤╡╫╩┴╧пер
16M33┐є┐и▓ё╙═╗·┐к╖в┼р╤╡╫╩┴╧пер Искусственный интеллект. Сценарий №1
Искусственный интеллект. Сценарий №1 Медицинское открытие. Бионические контактные линзы
Медицинское открытие. Бионические контактные линзы Ускорение свободного падения на Земле идругих небесных телах
Ускорение свободного падения на Земле идругих небесных телах Физика вокруг нас
Физика вокруг нас Монтаж электропривода
Монтаж электропривода