связано с окружающей нас природой и возможность использования этих сил человеком.
Цель урока: показать разнообразие сил, описываемых с помощью векторов.
Тема урока: Скорость прямолинейного равноускоренного движения. График скорости.
Ход урока:
1. Понятие вектора.
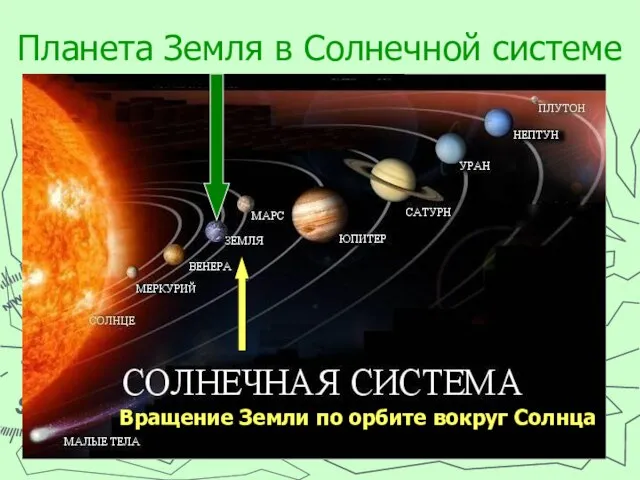
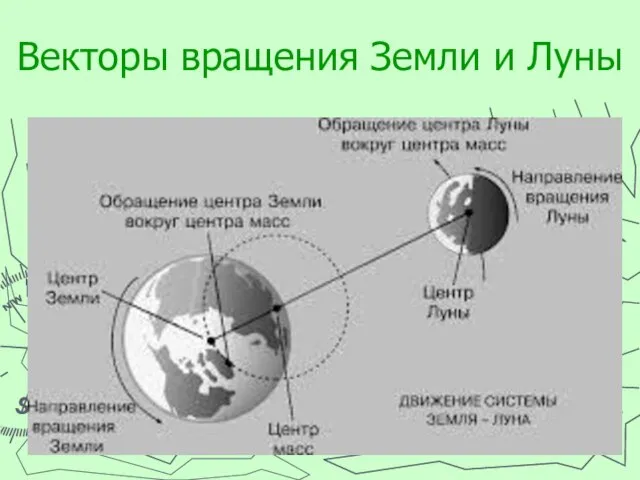
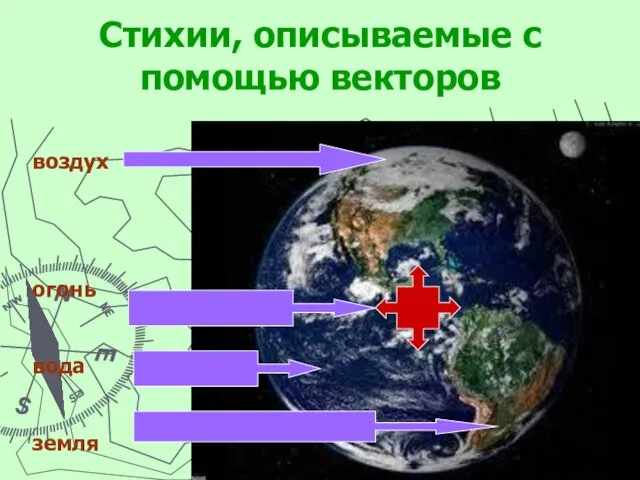
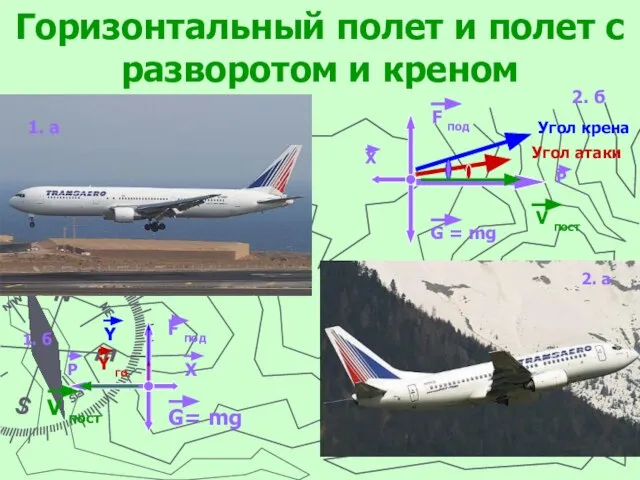
2. Вектор и окружающий нас мир.
3. Графическое изображение векторов.
4. Различные процессы, математически описываемые с помощью векторов.
5. Вывод.
Рефлексия: привести свой пример явления или процесса, который может быть описан с помощью векторов.
Из определения ускорения
при прямолинейном равноускоренном движении проекцию вектора ускорения на ось Х (т.к тело двигалось вдоль оси ОХ), можно найти по формуле.
Выразим из этой формулы проекцию Vx вектора скорости V, которую имеет движущееся тело к моменту времени t, если в начальный момент наблюдения to=Ос.
Можно записать уравнение нахождение скорости, в каждый момент времени
V(t)= V0 + at
Так как тело движется вдоль оси ОХ, то через проекции VX , V0x , aX, запишем
VХ = V0Х + axt
Если в начальный момент времени V0=0, то VX= aXt
Из курса математики известна линейная функция y= kx + b,
где x - аргумент, k - постоянный член, b - свободный член.
Графиком функции y (x) является прямая, по аналогии с графиком V(t) тоже является прямая:
где t- аргумент,
aX - постоянный коэффициент,
V0X - свободный член.












 Индивидуальное задание для практики (2)
Индивидуальное задание для практики (2) Презентация на тему Инфразвук
Презентация на тему Инфразвук  Презентация на тему Квантовая физика
Презентация на тему Квантовая физика  Эксплуатация аккумуляторов
Эксплуатация аккумуляторов Пара сил. Момент пары сил. Свойства пар сил. Момент силы относительно точки
Пара сил. Момент пары сил. Свойства пар сил. Момент силы относительно точки Организация технического обслуживания и диагностики с разработкой шиномонтажного стенда
Организация технического обслуживания и диагностики с разработкой шиномонтажного стенда Основы термодинамики. Тема № 4
Основы термодинамики. Тема № 4 Электрическая цепь. Последовательное и параллельное соединение проводников
Электрическая цепь. Последовательное и параллельное соединение проводников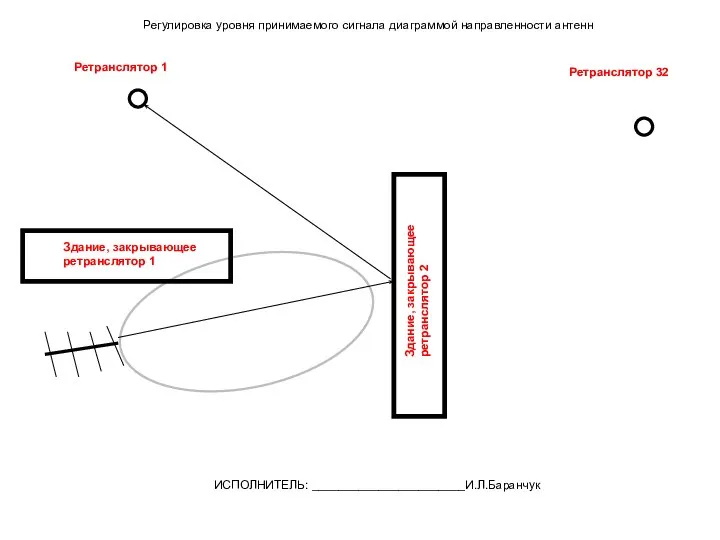 Приём отражённого сигнала в городе
Приём отражённого сигнала в городе Уравнение теплового баланса. Алгоритм решения задач
Уравнение теплового баланса. Алгоритм решения задач Плотность. Плотность мрамора
Плотность. Плотность мрамора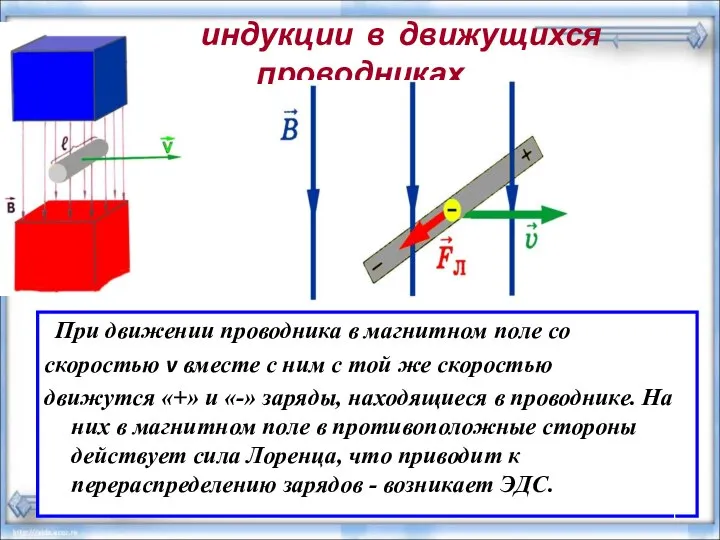 Вихревое электрическое поле. ЭДС индукции в движущихся проводниках
Вихревое электрическое поле. ЭДС индукции в движущихся проводниках График плавления и отвердевания кристаллических тел
График плавления и отвердевания кристаллических тел Звуки природы и звуки космоса. Что их объединяет
Звуки природы и звуки космоса. Что их объединяет Наглядное пособие для изучения шпоночного и штифтового соединений
Наглядное пособие для изучения шпоночного и штифтового соединений Техника безопасности при работе в лаборатории
Техника безопасности при работе в лаборатории Презентация на тему Перемещение при прямолинейном равноускоренном движении (9 класс)
Презентация на тему Перемещение при прямолинейном равноускоренном движении (9 класс)  Цепи переменного тока с последовательным соединением элементов
Цепи переменного тока с последовательным соединением элементов Уравнения Максвелла
Уравнения Максвелла Сила. Силы в природе и Работа. Мощность
Сила. Силы в природе и Работа. Мощность Метод размерностей
Метод размерностей Свет. Источники света. Звезда-Солнце. Солнечные и лунные затмения
Свет. Источники света. Звезда-Солнце. Солнечные и лунные затмения Инерционные силы
Инерционные силы Количество теплоты. Единицы количества теплоты. Удельная теплоемкость
Количество теплоты. Единицы количества теплоты. Удельная теплоемкость Тепловые двигатели
Тепловые двигатели Расчет силы тока и напряжения в электрических цепях
Расчет силы тока и напряжения в электрических цепях Lect_2
Lect_2 Давление света
Давление света