законов этой дисциплины, представляющий собой конкретизацию общефизического закона сохранения энергии (первый закон термодинамики) — один из основных законов этой дисциплины, представляющий собой конкретизацию общефизического закона сохранения энергии для термодинамических систем (первый закон термодинамики) — один из основных законов этой дисциплины, представляющий собой конкретизацию общефизического закона сохранения энергии для термодинамических систем, в которых необходимо учитывать термические (первый закон термодинамики) — один из основных законов этой дисциплины, представляющий собой конкретизацию общефизического закона сохранения энергии для термодинамических систем, в которых необходимо учитывать термические, массообменные (первый закон термодинамики) — один из основных законов этой дисциплины, представляющий собой конкретизацию общефизического закона сохранения энергии для термодинамических систем, в которых необходимо учитывать термические, массообменные и химические процессы.
В форме закона сохранения (уравнения баланса энергии) первое начало используют в термодинамике потокаВ форме закона сохранения (уравнения баланса энергии) первое начало используют в термодинамике потока и в неравновесной термодинамике.
В равновесной термодинамике под первым законом термодинамики обычно подразумевают одно из следствий закона сохранения энергии, из чего проистекает отсутствие единообразия формулировок первого начала, используемых в учебной и научной литературе (К. А. Путилов в своей монографии[1] приводит шесть формулировок, которые он считает наиболее удачными).
[1] - Путилов К. А., Термодинамика, 1971, с. 39—40.
В общем виде формулировка первого закона термодинамики будет звучать примерно так:
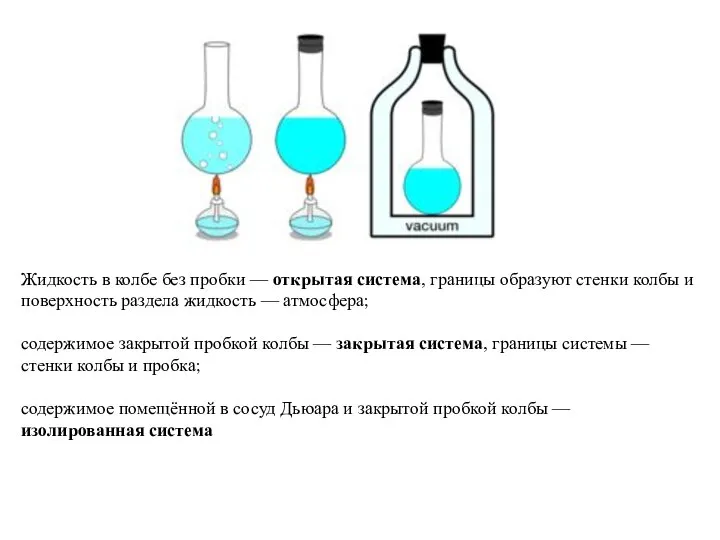
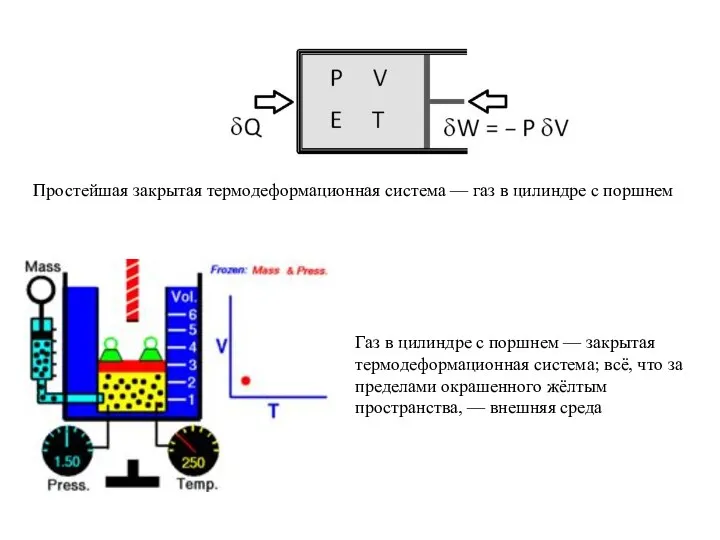
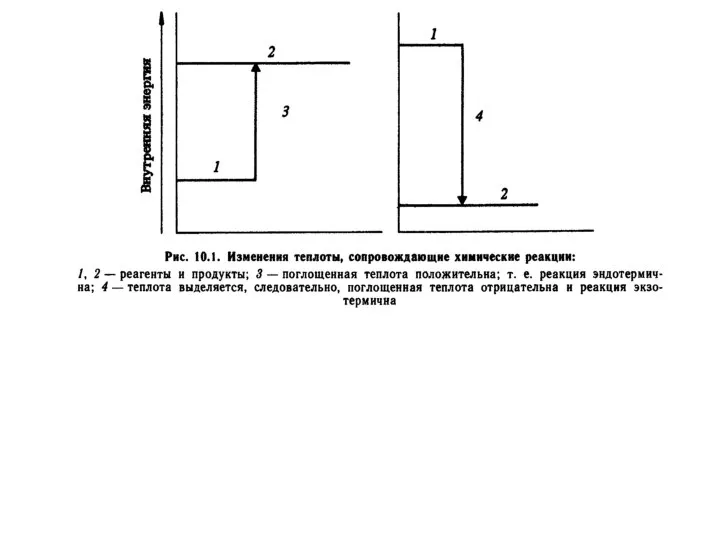
Изменение внутренней энергии системы при переходе из одного состояния в другое равно сумме количества теплоты, подведенной к системе извне и работе действующих на нее внешних сил.
























































 Применение неметаллов
Применение неметаллов Общая характеристика элементов подгруппы углерода. Углерод – его строение и свойства
Общая характеристика элементов подгруппы углерода. Углерод – его строение и свойства Азотная кислота
Азотная кислота Презентация на тему Химия и повседневная жизнь человека
Презентация на тему Химия и повседневная жизнь человека  Металлы. Общая характеристика, химические свойства. Получение
Металлы. Общая характеристика, химические свойства. Получение Самостоятельная работа
Самостоятельная работа Выберите вещества
Выберите вещества История развития химии
История развития химии Газовые смеси. Способы задания газовых смесей. Лекция 5
Газовые смеси. Способы задания газовых смесей. Лекция 5 Металлическая, водородная, Ван-дер-ваальсова химические связи
Металлическая, водородная, Ван-дер-ваальсова химические связи Презентация на тему Азотная кислота
Презентация на тему Азотная кислота  Характеристика нефти и ее фракций как сырья для производства мoторныx топлив. Тема 2
Характеристика нефти и ее фракций как сырья для производства мoторныx топлив. Тема 2 Общие представления об электрохимических технологиях
Общие представления об электрохимических технологиях Строение атома
Строение атома Новогодний Пробник №190415
Новогодний Пробник №190415 Сложные вещества оксиды
Сложные вещества оксиды Презентация на тему Строение и свойства циклоалканов
Презентация на тему Строение и свойства циклоалканов  Диэлектрики
Диэлектрики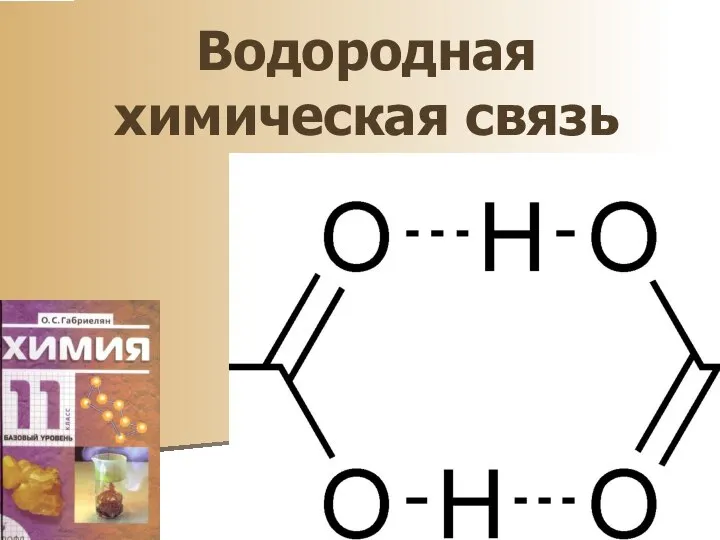 Водородная химическая связь
Водородная химическая связь Презентация на тему Альдегиды и их свойства
Презентация на тему Альдегиды и их свойства  Гималайская соль
Гималайская соль proekt_TTU_3_1
proekt_TTU_3_1 от греч. Hydro –вода, Lysis – разложение, распад Гидролиз – это реакция обменного разложения веществ водой
от греч. Hydro –вода, Lysis – разложение, распад Гидролиз – это реакция обменного разложения веществ водой Маска откройся
Маска откройся Титриметрический анализ. Основные понятия
Титриметрический анализ. Основные понятия Фенолы
Фенолы 1666603286718__4v20ts
1666603286718__4v20ts Практическое пособие по твердофазной экстракции
Практическое пособие по твердофазной экстракции