Содержание
- 2. Что будем рассматривать? Что такое ЯЗЫК? Какие существуют ФОРМАЛЬНЫЕ СПОСОБЫ описания языков? Что такое ЯЗЫК ПРОГРАММИРОВАНИЯ
- 3. Структура курса (учебный план 09.03.04 ) Семестр 16 недель Лекции: 32 часа (1 пара в неделю)
- 4. Лабораторные работы 1 (2 часа) Синтез КС-грамматик 2 (2 часа) КС-грамматика языка программирования 3 (2 часа)
- 5. Отчеты по работам Отчет по каждой работе в электронном виде должен быть оформлен и сдан: Отчет
- 6. Задания №1 и №2 Задание №1 (работа №1) – в учебнике. Залание №2 (работы 2-15) -
- 7. Задание по трансляторам В каждом задании описывается некоторый очень усеченный вариант известных языков программирования Java и
- 8. Пример задания по трансляторам Программа: главная программа языка С++. Допускается описание функций без параметров, функции возвращают
- 9. Обратите внимание на полноту реализации задания во всех заданиях предполагается использование составного и пустого оператора, всегда
- 10. Тема 1 Формальные грамматики и языки
- 11. Базовые понятия Алфавит - непустое конечное множество символов. Цепочка над алфавитом Σ - конечная последовательность символов
- 12. Примеры алфавита Алфавит Σ = {0,1} Σ* = {ε , 0, 1 ,00, 01, 10, 11,
- 13. Грамматика Порождающая грамматика - упорядоченная четверка G = (VT , VN ,P ,S), где VT -
- 14. Типы G = (VT , VN ,P ,S) Тип грамматики определяется сложностью правил P ={u ?
- 15. Пример грамматики G = (VT ,VN ,P ,S), где VT = {0,1,…,9,x,a,…f} VN = {S, H,
- 16. Обозначение нетерминалов Вариант 1 - большие латинские буквы (при условии их отсутствия в VT) G: S
- 17. Правила КС-грамматики G = (VT ,VN ,P ,S) конструкция правила ? Пример S ? SaB |
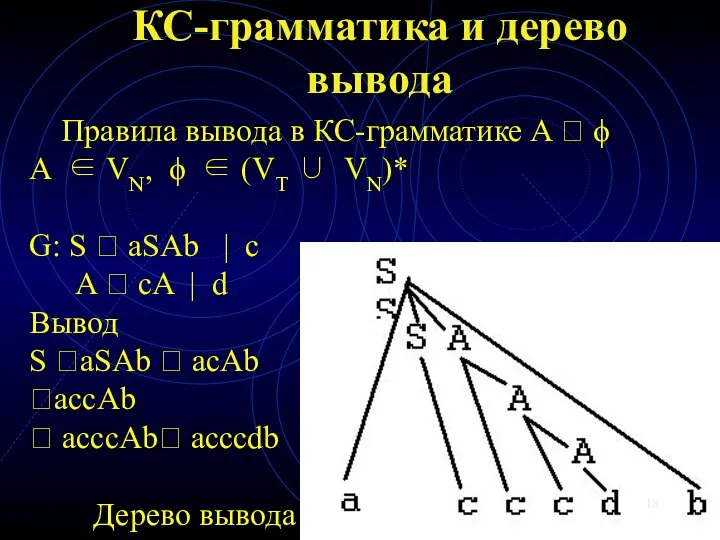
- 18. КС-грамматика и дерево вывода Правила вывода в КС-грамматике A ? ϕ A ∈ VN, ϕ ∈
- 19. Операции над языками 1) Обычные теоретико-множественные: Объединение L1 ∪ L2 Пересечение L1 ∩ L2 Разность L1
- 20. Операции – инструмент синтеза КСГ Теорема Семейство КС-языков замкнуто относительно операций объединения, произведения, итерации и усеченной
- 21. Доказательство для L1 L2 Конкатенация (умножение) Дано: G1 = (VT1 ,VN1 ,P1 ,S1), G2 = (VT2
- 22. Доказательство для L1 ∪ L2 Объединение Дано: G1 = (VT1 ,VN1 ,P1 ,S1), G2 = (VT2
- 23. Доказательство для L* Итерация Дано: G1 = (VT1 ,VN1 ,P1 ,S1) Нужна грамматика языка L(G) =
- 24. Правая рекурсия для L* Итерация Дано: G1 = (VT1 ,VN1 ,P1 ,S1) Нужна грамматика языка L(G)
- 25. Доказательство для L+ Усеченная итерация Дано: G1 = (VT1 ,VN1 ,P1 ,S1) Нужна грамматика языка L(G)
- 26. Правая рекурсия для L+ Усеченная итерация Дано: G1 = (VT1 ,VN1 ,P1 ,S1) Нужна грамматика языка
- 27. Пример: язык (ab)*c ∪ b+ G: S ? A | B // объединение (ab)*c и b+
- 28. Пример: идентификатор С++ Идентификатор – это последовательность букв и цифр, начинающаяся с буквы. Знак подчеркивания рассматривается
- 29. Симметрия в языке L = αnγβn , n >= 0 S ? αSβ | γ Вывод
- 30. Простой пример симметрии Симметричные конструкции S ? ASB | X L(S) = L(A)n L(X) L(B)n n
- 31. Пример симметрии L = a2nd(a+b*с)n+1 , n >= 0 Выделим симметрию L = a2nd(a+b*с)n+1 = (aa)n
- 32. Преобразования КСГ Подстановки Новые нетерминалы для фрагментов Неукорачивание Левая рекурсия ? правая Правая рекурсия ? левая
- 33. Левая рекурсия ? правая Были правила S ? SA | B Вывод: S ? SA ?
- 34. Левая рекурсия ? правая (Общий случай) Были правила S ? Sβ1 | Sβ2 | … |
- 35. Правая рекурсия ? левая (Общий случай) Были правила S ? β1S | β2S | … |
- 36. Рекурсия Грамматика конечна по опреледению. Язык, как правило, бесконечен. Рекурсия – единственный способ представить бесконечный язык
- 37. Рекурсия конструкций ЯП ? | | ? ; ? { } ? | | |… ?
- 38. Синтаксический анализ Задача любого транслятора – построить дерево грамматического разбора. Если язык бесконечен, а КС-грамматика конечна,
- 39. Лемма о разрастании Для любой КС - грамматики, порождающей бесконечный язык, существуют такие натуральные числа p
- 40. Следствие – теорема о языке anbncn Теорема Язык anbncn не является КС-языком. Вывод: КС-грамматика не может
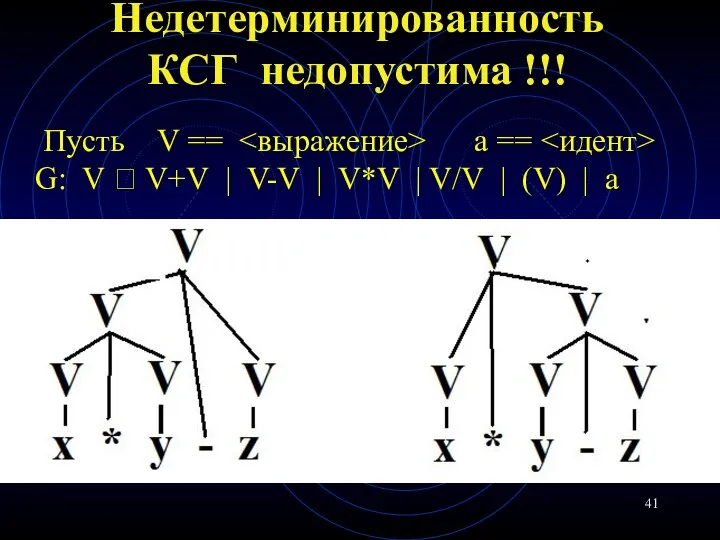
- 41. Недетерминированность КСГ недопустима !!! Пусть V == a == G: V ? V+V | V-V |
- 42. Выражения Нет понятия логического, арифметического и т.п. выражения: Работает семантика контекстных условий для контроля корректности выражений:
- 43. Синтаксис выражений 1 Упорядочить группы операций по приоритетам, начиная с низкоприоритетных . 2 Каждой группе поставить
- 44. Правила для группы многократных операций Операции многократные, т.е. разрешается запись а*а*а*а Операция бинарная выполнение слева направо
- 45. Правила для группы однократных операций Операции однократные, т.е. НЕ разрешается запись а*а*а*а Операция бинарная Ai ?
- 46. Пример выражения с бинарными операциями A1 > A2 + - A3 * / A1 ? A1
- 47. Лабораторная работа №1 1. Построить КС-грамматику по заданию в учебнике (№ задания == номер в списке
- 48. Лабораторная работа № 2 1. Построить таблицу приоритетов операций языка программирования индивидуального задания 2. Построить КС-грамматику
- 49. Языки, грамматика, автоматы Грамматика порождает язык Автомат распознает язык Программист использует (1) при создании программы Транслятор
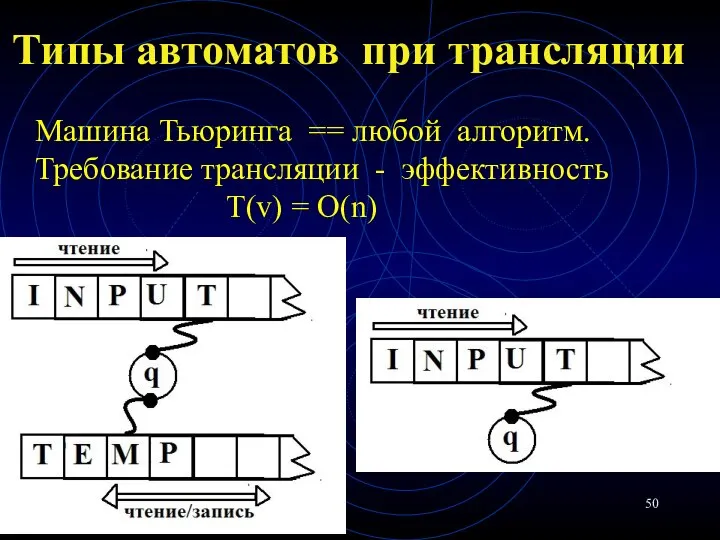
- 50. Типы автоматов при трансляции Машина Тьюринга == любой алгоритм. Требование трансляции - эффективность T(v) = O(n)
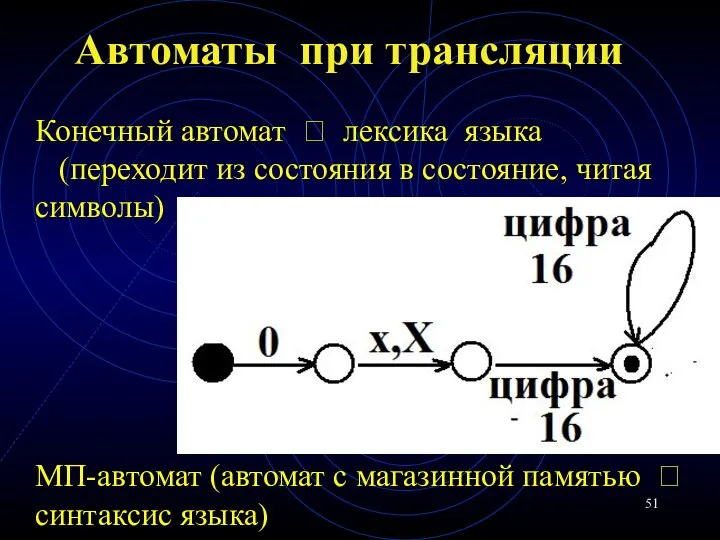
- 51. Автоматы при трансляции Конечный автомат ? лексика языка (переходит из состояния в состояние, читая символы) МП-автомат
- 52. Синтез конечных автоматов Учебное пособие (содержит теоретический материал и примеры): глава 2
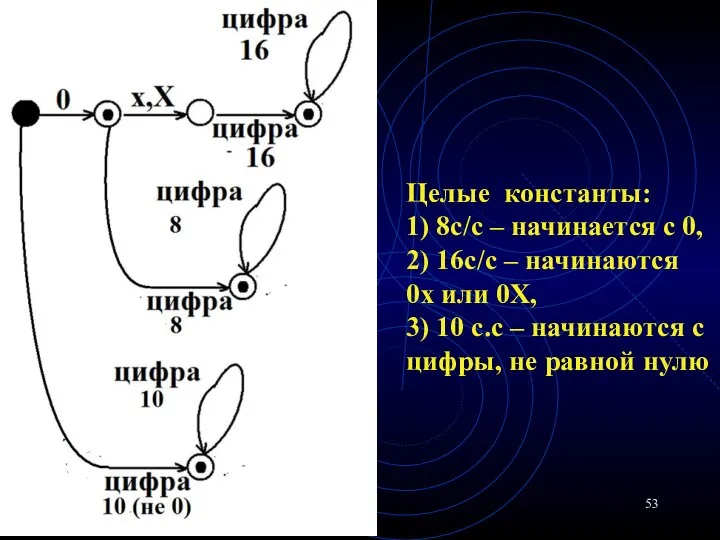
- 53. Целые константы: 1) 8с/с – начинается с 0, 2) 16c/c – начинаются 0x или 0X, 3)
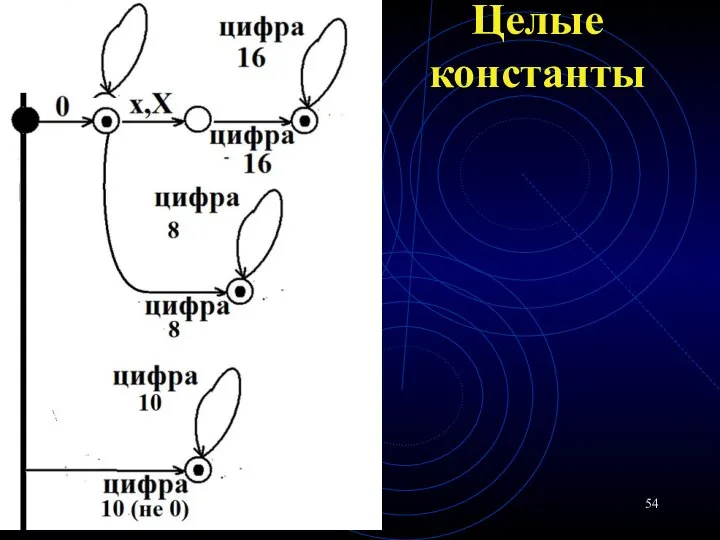
- 54. Целые константы
- 56. Скачать презентацию















































 Точки и вектора. Геометрия
Точки и вектора. Геометрия Анализ конкретной стратегии изданий на платформах разного типа
Анализ конкретной стратегии изданий на платформах разного типа POS кредит для интернет магазинов
POS кредит для интернет магазинов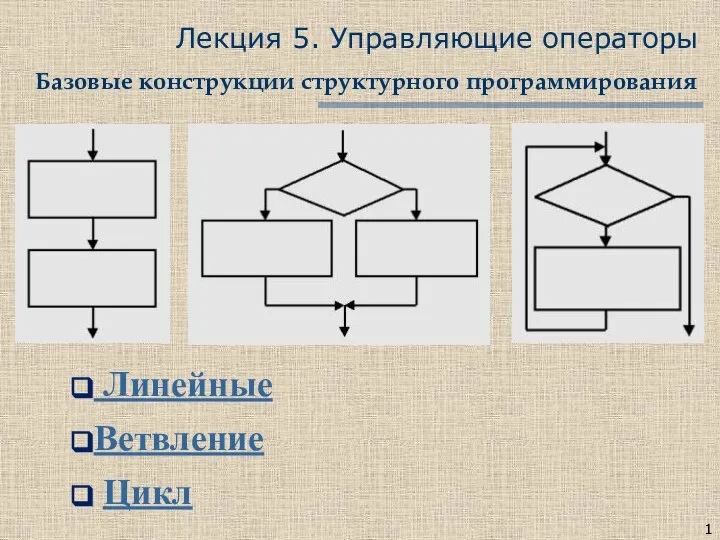 Управляющие операторы. Базовые конструкции структурного программирования. Лекция 5
Управляющие операторы. Базовые конструкции структурного программирования. Лекция 5 Информационные ресурсы
Информационные ресурсы Generation of the 21st century
Generation of the 21st century Алгоритмизация и программирование
Алгоритмизация и программирование Сортировка массива
Сортировка массива Устройства хранения данных. Файлы и папки. Работа с файловым менеджером и программами-утилитами операционной системы
Устройства хранения данных. Файлы и папки. Работа с файловым менеджером и программами-утилитами операционной системы Введение в информационную безопасность. Основы защиты информации
Введение в информационную безопасность. Основы защиты информации Система поддержки принятия решений. Электромеханика
Система поддержки принятия решений. Электромеханика dz Python (1)
dz Python (1) Использование компьютерных программ в графическом дизайне
Использование компьютерных программ в графическом дизайне RedeX Plus
RedeX Plus Как заполнить Google форму?
Как заполнить Google форму? Европейский Север. От западных границ до Урала
Европейский Север. От западных границ до Урала Программное обеспечение компьютера
Программное обеспечение компьютера Рекомендации по действиям при взломе аккаунта и созданию
Рекомендации по действиям при взломе аккаунта и созданию Использование сайта педагога как актуальный ресурс для коммуникации
Использование сайта педагога как актуальный ресурс для коммуникации Создание презентаций с помощью MS PowerPoint
Создание презентаций с помощью MS PowerPoint Презентация на тему Основные понятия и правила записи функций в Excel
Презентация на тему Основные понятия и правила записи функций в Excel  Презентация на тему Кодирование информации
Презентация на тему Кодирование информации  Технология создания и обработки графической информации. Лекция 2
Технология создания и обработки графической информации. Лекция 2 Визуальное программирование. Среда программирования Scratch 3.17.2
Визуальное программирование. Среда программирования Scratch 3.17.2 Презентация на тему Классификация компьютеров
Презентация на тему Классификация компьютеров  Эффективность применения штрихового кодирования в России
Эффективность применения штрихового кодирования в России Единицы измерения информации
Единицы измерения информации Механика работы активности
Механика работы активности