10-18-1-algebra-logiki_1

Ключевые слова
логическое высказывание
логическая операция
логическая переменная
предикат

Алгебра логики
Джордж Буль (1815-1864) – английский математик, основоположник алгебры логики. Изучал логику мышления матема-тическими методами и разработал алгебраические методы решения тради-ционных логических задач. Долгое время алгебра логики была известна достаточно узкому классу специалистов.
В 1938 году Клод Шеннон применил алгебру логики для описания процесса функционирования релейно-контактных и электронно-ламповых схем.

Высказывания и переменные

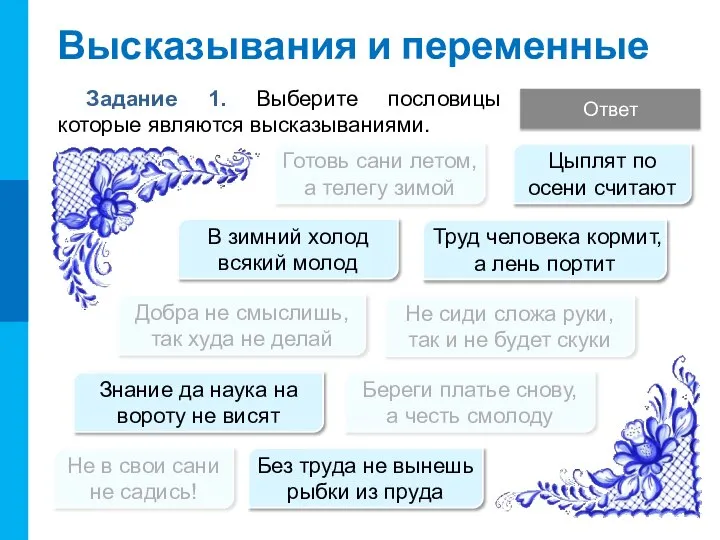
Высказывания и переменные
Задание 1. Выберите пословицы которые являются высказываниями.
Знание да наука на вороту не висят
Береги платье снову,
а честь смолоду
Труд человека кормит, а лень портит
Готовь сани летом, а телегу зимой
Не сиди сложа руки, так и не будет скуки
Добра не смыслишь, так худа не делай
Цыплят по осени считают
В зимний холод
всякий молод
Не в свои сани не садись!
Без труда не вынешь рыбки из пруда
Ответ

Высказывания и переменные
Истинность или ложность составных высказываний зависит от истинности или ложности образующих их высказываний и определённой трактовки связок (логических операций над высказываниями).

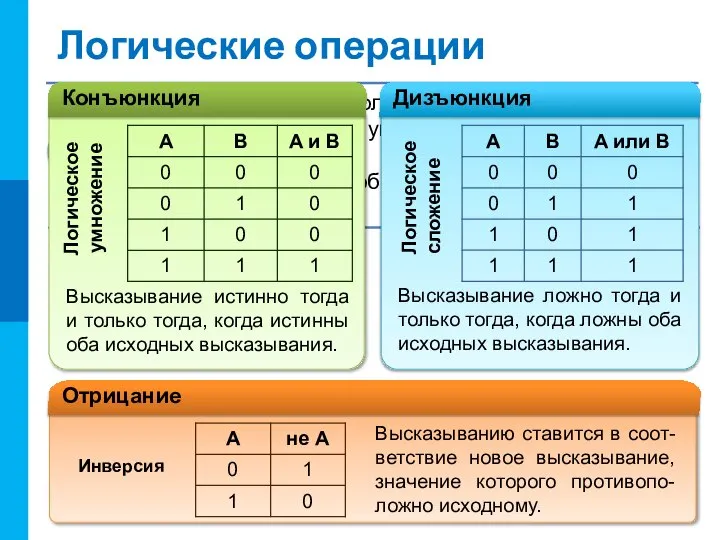
Логические операции
Высказывание истинно тогда и только тогда, когда истинны оба исходных высказывания.
Высказывание ложно тогда и только тогда, когда ложны оба исходных высказывания.
Логическое
умножение
Логическое
сложение
Высказыванию ставится в соот-ветствие новое высказывание, значение которого противопо-ложно исходному.
Инверсия

Логические операции
Ложно тогда и только тогда, когда посылка (первое) истинна, а следствие (второе) ложно.
Следование
Пример высказывания:
Если верно списали пример, то получили верный ответ.
A: Пример списали верно
B: Получили верный ответ
В высказывании нет информации о правильности самого решения. Анализи-ровать можно только то, что сказано в высказывании.
Если списали неверно, то ответ может быть любым.
Из ложной посылки можно получить истинное и ложное высказывание, из истинного только истинное.

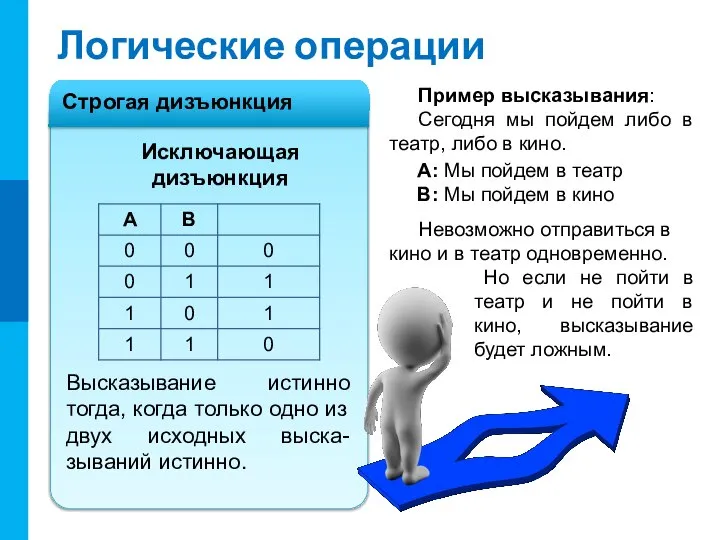
Логические операции
Высказывание истинно тогда, когда только одно из двух исходных выска-зываний истинно.
Исключающая дизъюнкция
Пример высказывания:
Сегодня мы пойдем либо в театр, либо в кино.
A: Мы пойдем в театр
B: Мы пойдем в кино
Невозможно отправиться в кино и в театр одновременно.
Но если не пойти в театр и не пойти в кино, высказывание будет ложным.

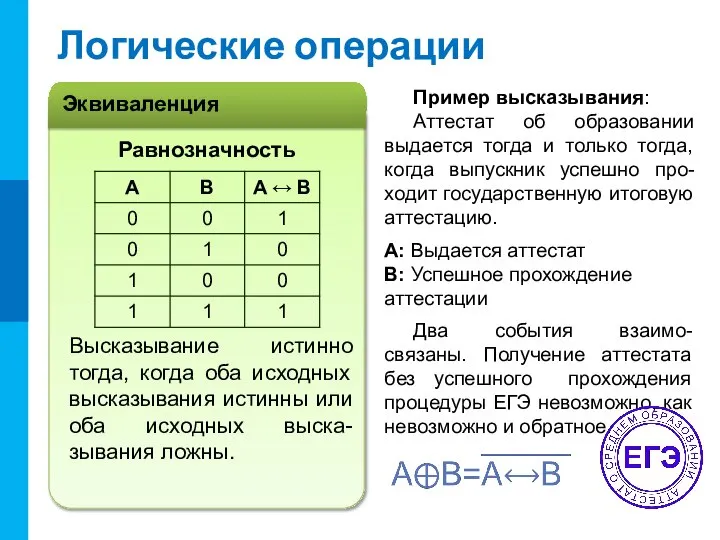
Логические операции
Высказывание истинно тогда, когда оба исходных высказывания истинны или оба исходных выска-зывания ложны.
Равнозначность
Пример высказывания:
Аттестат об образовании выдается тогда и только тогда, когда выпускник успешно про-ходит государственную итоговую аттестацию.
A: Выдается аттестат
B: Успешное прохождение аттестации
Два события взаимо-связаны. Получение аттестата без успешного прохождения процедуры ЕГЭ невозможно, как невозможно и обратное.

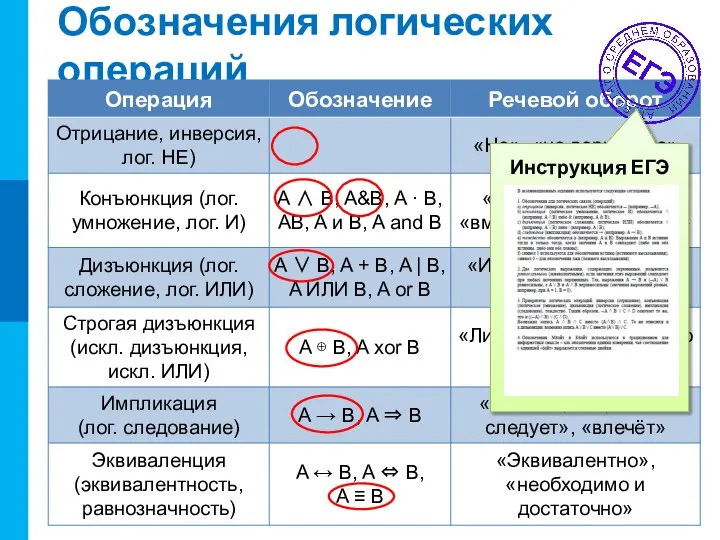
Обозначения логических операций

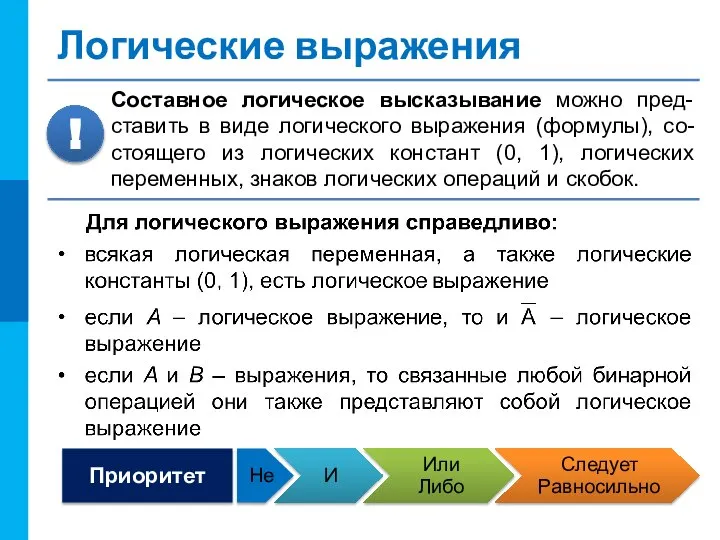
Логические выражения
Не
И
Или
Либо
Следует
Равносильно
Приоритет

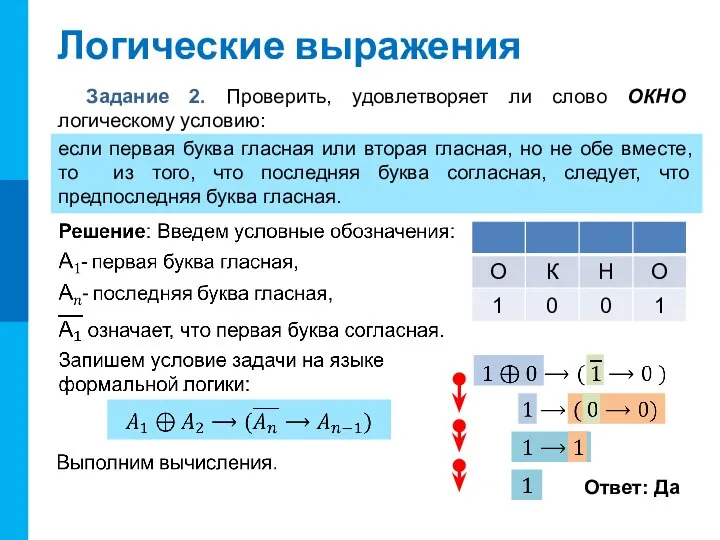
Логические выражения
Задание 2. Проверить, удовлетворяет ли слово ОКНО логическому условию:
если первая буква гласная или вторая гласная, но не обе вместе, то из того, что последняя буква согласная, следует, что предпоследняя буква гласная.
Ответ: Да

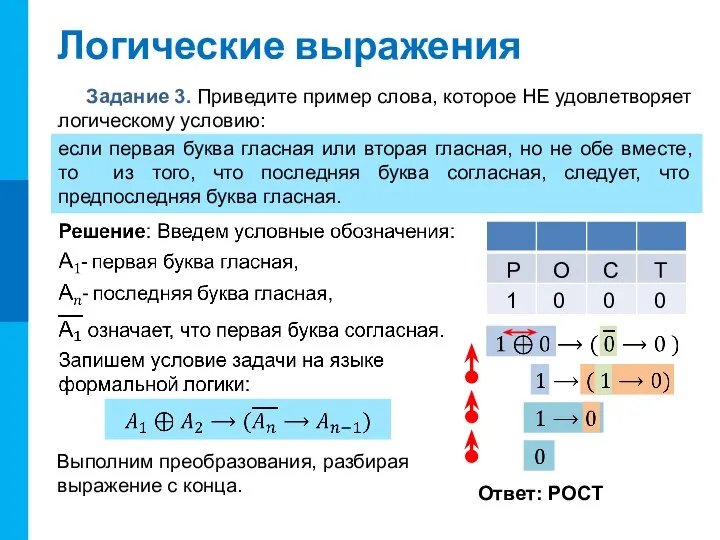
Логические выражения
Задание 3. Приведите пример слова, которое НЕ удовлетворяет логическому условию:
если первая буква гласная или вторая гласная, но не обе вместе, то из того, что последняя буква согласная, следует, что предпоследняя буква гласная.
Выполним преобразования, разбирая выражение с конца.
Ответ: РОСТ
1
0
0
0
Р
О
С
Т

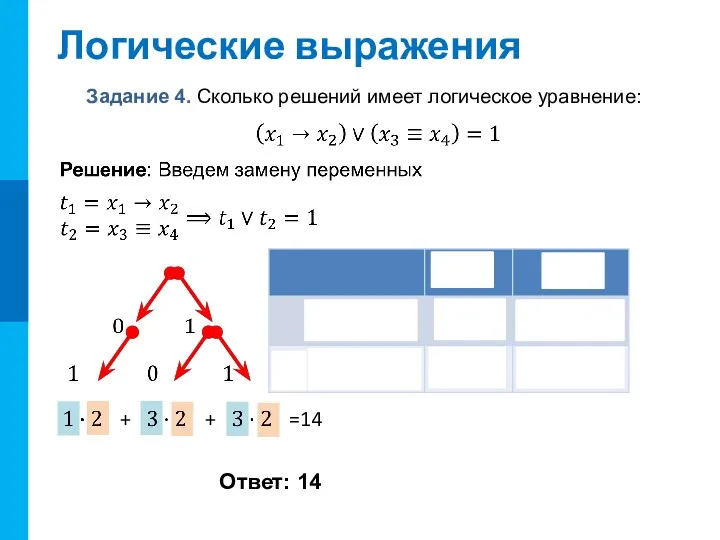
Логические выражения
Задание 4. Сколько решений имеет логическое уравнение:
Ответ: 14
+
+
=14

Предикаты и множества истинности
Ответ

Самое главное
Высказывание – это предложение, в отношении которого можно сказать, истинно оно или ложно. Высказывания, образованные из других высказываний, называются составными. Высказывание, никакая часть которого не является высказыванием, называется элементарным.
Истинность или ложность составных высказываний зависит от истинности или ложности образующих их высказываний и логических операций над высказываниями.
Логическая операция полностью может быть описана таблицей истинности, указывающей, какие значения принимает составное высказывание при всех возможных значениях образующих его элементарных высказываний.

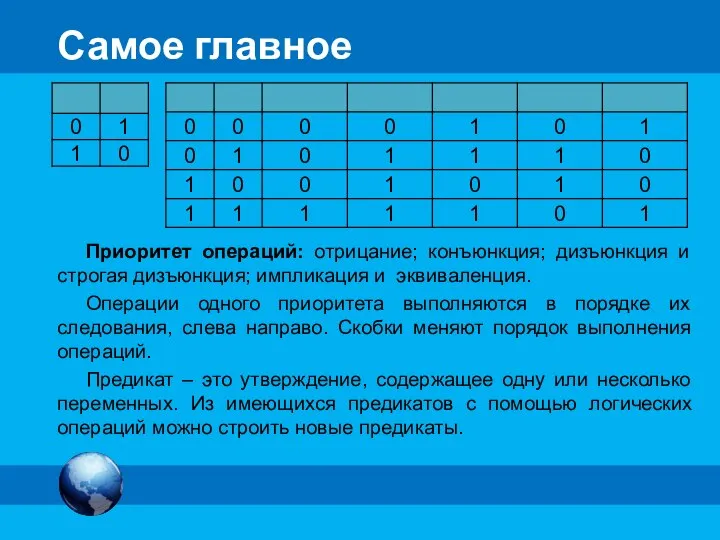
Самое главное
Приоритет операций: отрицание; конъюнкция; дизъюнкция и строгая дизъюнкция; импликация и эквиваленция.
Операции одного приоритета выполняются в порядке их следования, слева направо. Скобки меняют порядок выполнения операций.
Предикат – это утверждение, содержащее одну или несколько переменных. Из имеющихся предикатов с помощью логических операций можно строить новые предикаты.

Вопросы и задания
Выбрать два противоположных высказывания:
Среди учеников деревни Сосновка только один добирается до школы на автобусе
Все ученики деревни Сосновка добираются до школы на автобусе
Никто из учеников деревни Сосновка не добирается до школы на автобусе
В деревне Сосновка есть хотя бы один ученик, который до школы добирается не на автобусе
Ответ
Ответ

Ответ: 12
Вопросы и задания
Сколько точек с целочисленными координатами удовлетворяют условию:
Решение
Ответ
Сколько решений имеет логическое уравнение:
Ответ: 1