Содержание
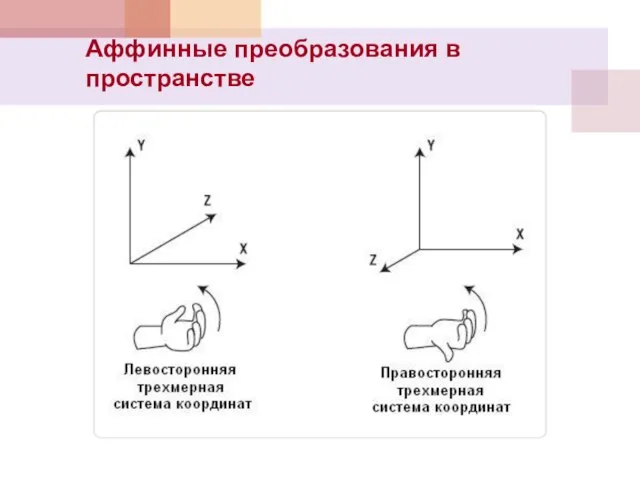
- 2. Аффинные преобразования в пространстве
- 3. Аффинные преобразования в пространстве I. Вращение в пространстве Матрица вращения вокруг оси абсцисс на угол ϕ
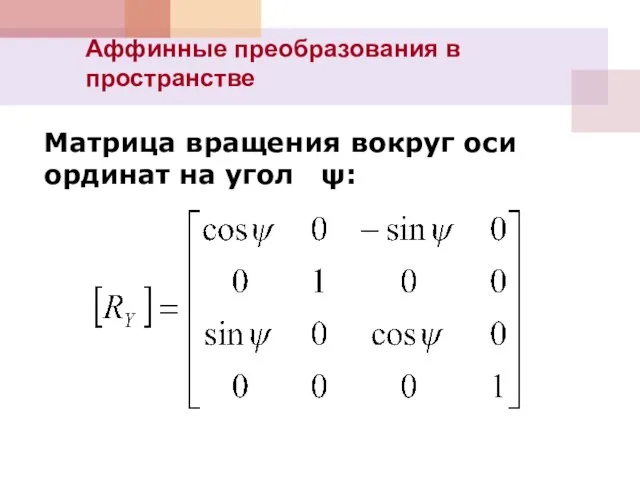
- 4. Аффинные преобразования в пространстве Матрица вращения вокруг оси ординат на угол ψ:
- 5. , Матрица вращения вокруг оси аппликат на угол θ: Аффинные преобразования в пространстве
- 6. Аффинные преобразования в пространстве II. Масштабирование: Коэффициенты: α>0 –вдоль оси абсцисс, β>0 –вдоль оси ординат, γ>0
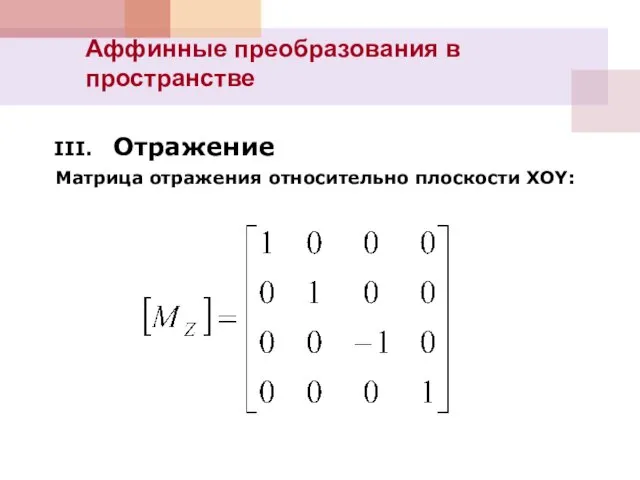
- 7. Аффинные преобразования в пространстве III. Отражение Матрица отражения относительно плоскости XOY:
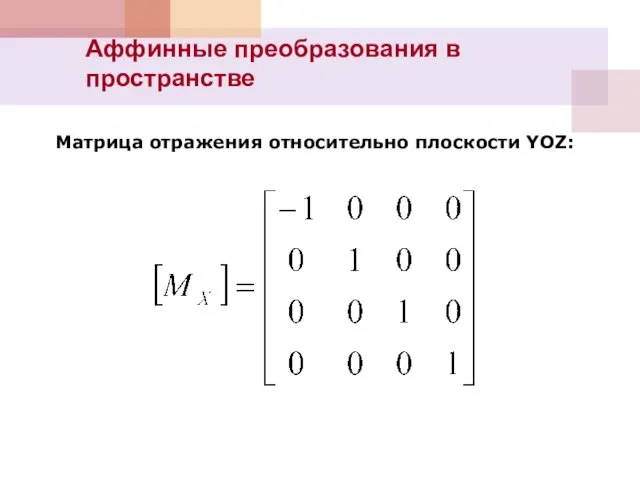
- 8. Матрица отражения относительно плоскости YOZ: Аффинные преобразования в пространстве
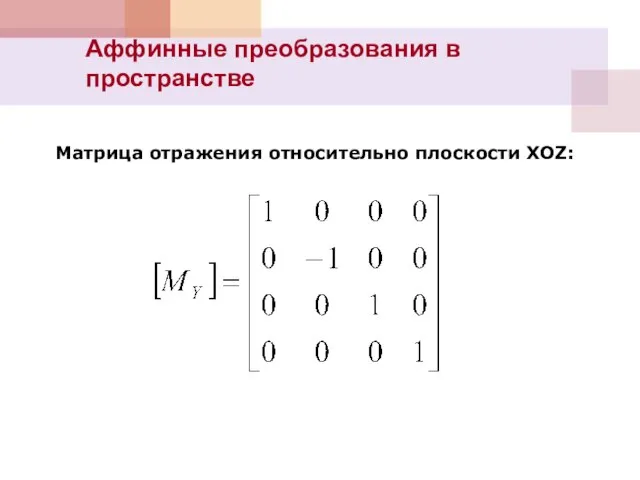
- 9. Аффинные преобразования в пространстве Матрица отражения относительно плоскости XOZ:
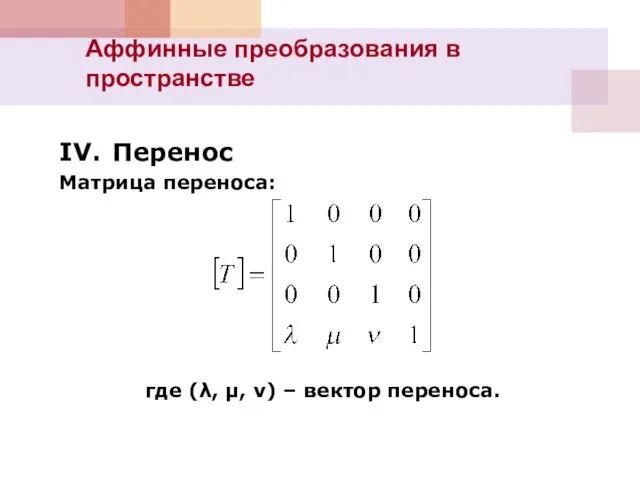
- 10. IV. Перенос Матрица переноса: где (λ, μ, ν) – вектор переноса. Аффинные преобразования в пространстве
- 11. ПРОЕКТИВНЫЕ ПРЕОБРАЗОВАНИЯ
- 12. МЕТОДЫ И АЛГОРИТМЫ ТРЕХМЕРНОЙ ГРАФИКИ
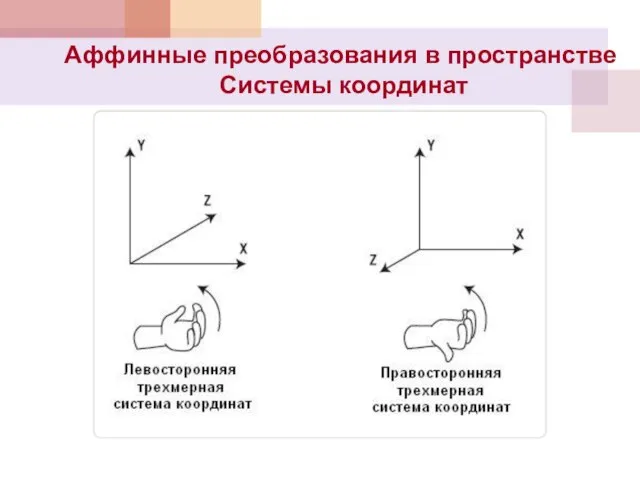
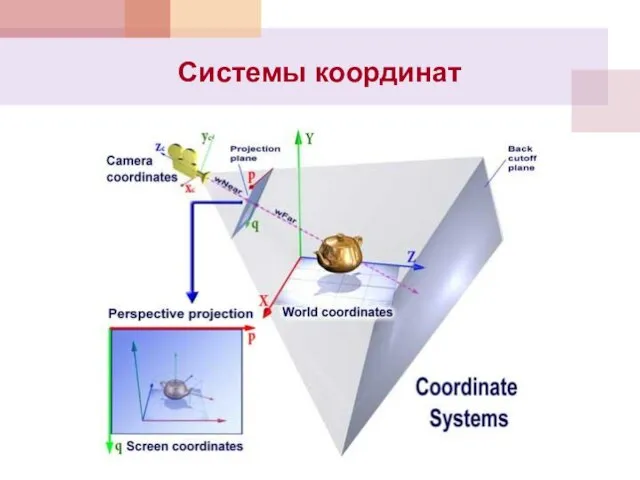
- 13. Аффинные преобразования в пространстве Системы координат
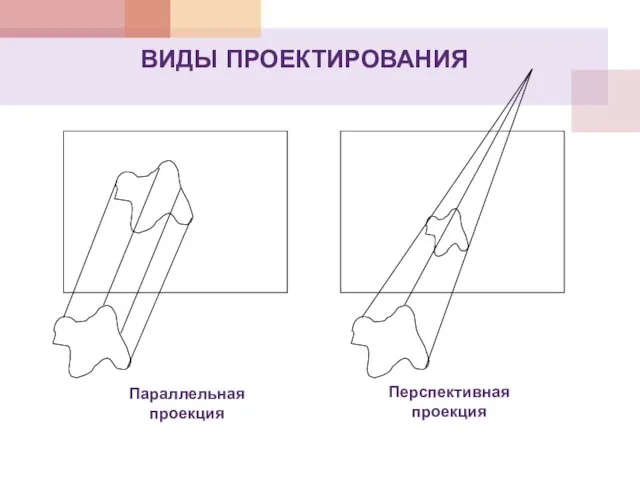
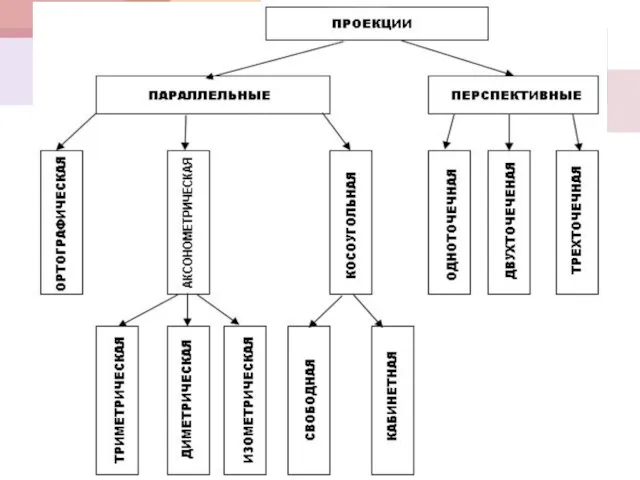
- 14. ВИДЫ ПРОЕКТИРОВАНИЯ
- 15. Преобразования координат
- 16. Системы координат
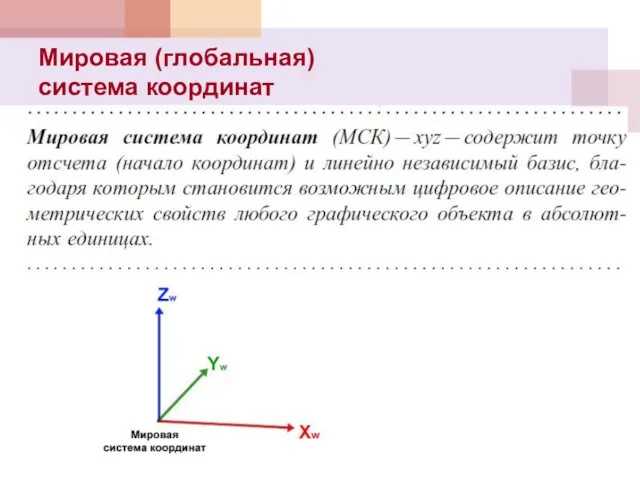
- 17. Мировая (глобальная) система координат
- 18. Экранная система координат
- 19. Система координат сцены
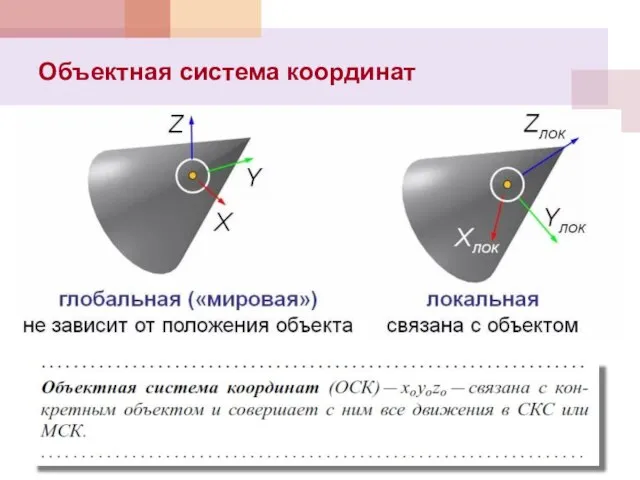
- 20. Объектная система координат
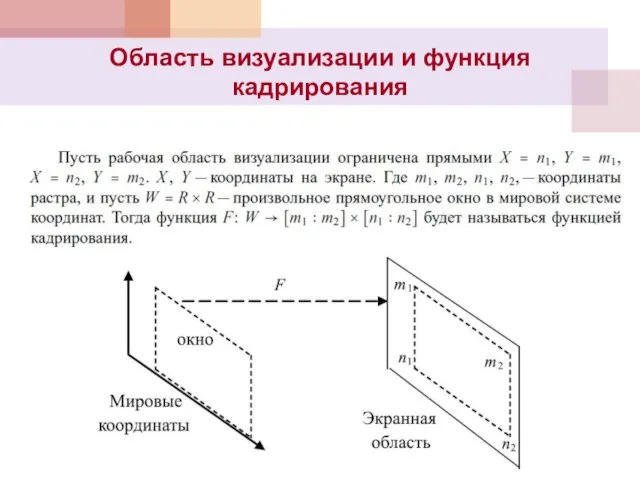
- 24. Область визуализации и функция кадрирования
- 25. Функция кадрирования
- 27. Параллельное проектирование Ортографическая проекция Матрица проектирования вдоль оси Х на плоскость YOZ
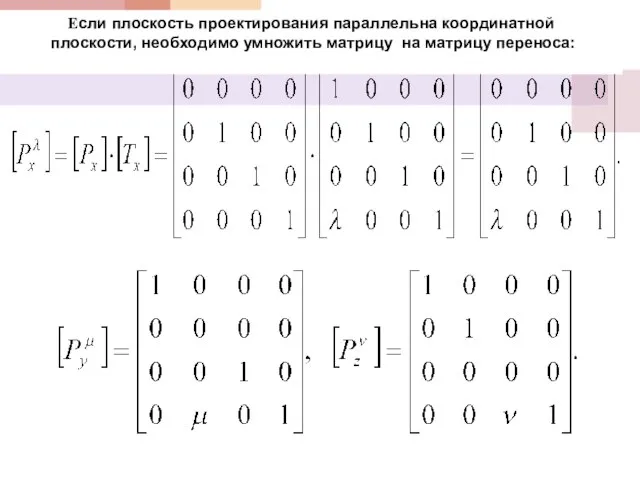
- 28. Если плоскость проектирования параллельна координатной плоскости, необходимо умножить матрицу на матрицу переноса:
- 29. Триметрия – нормаль к картинной плоскости образует с ортами координатных осей попарно различные углы. Аксонометрическая проекция
- 30. Диметрия – два угла между нормалью к картинной плоскости и координатными осями равны. Аксонометрическая проекция
- 31. Аксонометрическая проекция Изометрия – все три угла между нормалью к картинной плоскости и координатными осями равны.
- 32. Параллельное проектирование Косоугольная проекция При косоугольном проектировании на плоскость XOY имеем: Матрица преобразования имеет вид:
- 33. Свободная проекция: Кабинетная проекция: Косоугольная проекция
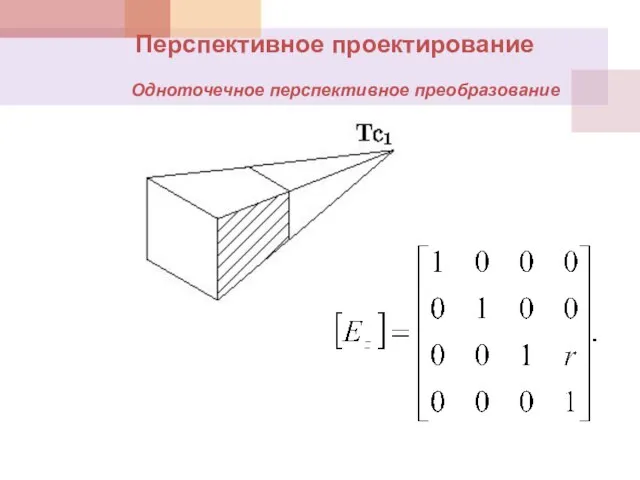
- 34. Перспективное проектирование Одноточечное перспективное преобразование
- 35. Одноточечное перспективное преобразование
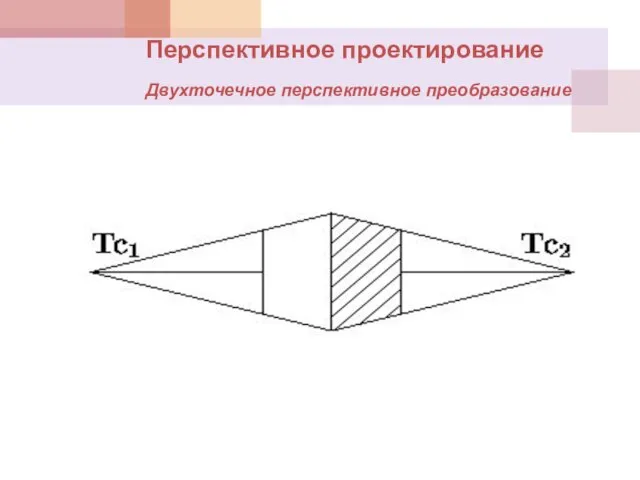
- 36. Перспективное проектирование Двухточечное перспективное преобразование
- 37. Двухточечное перспективное преобразование
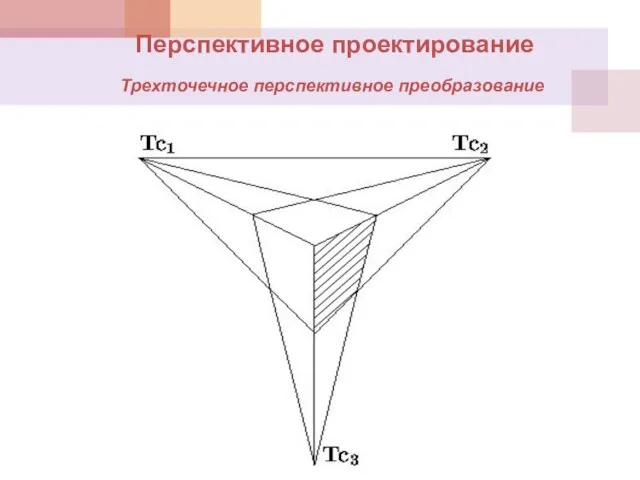
- 38. Перспективное проектирование Трехточечное перспективное преобразование
- 39. на оси x: на оси y: на оси z: .
- 40. OpenGL (Open Graphic Library) – библиотека графических функций, интерфейс для графических прикладных программ.
- 41. Open Graphics Library — открытая графическая библиотека, графическое API — спецификация, определяющая независимый от языка программирования
- 42. Включает более 250 функций для рисования сложных трёхмерных сцен из простых (2D) примитивов. Используется при создании
- 43. OpenGL 1.0 Silicon Graphics Incorporated (SGI) 1992 г. OpenGL 2.0 3DLabs 2001 г. OpenGL 3.0 Khronos
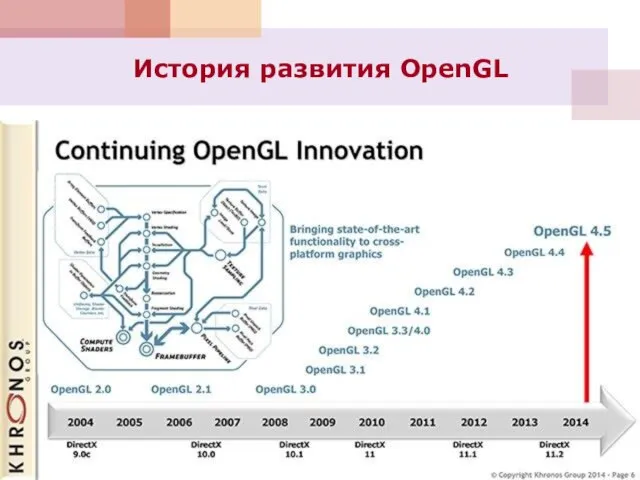
- 44. История развития OpenGL 2015 Mantle - спецификация низкоуровневого API, разработанная компанией AMD в качестве альтернативы DirectX
- 45. MoltenVK Единственная возможность работать с Vulkan на MacOS Стоисть ≈250$ Работает с потерей производительности
- 46. Ручное управление памятью Отсутствие проверок в драйвере Спроектирован для многопоточности
- 47. - Vulkan это: а) Лишь стандарт, а значит реализация лежит на разработчиках драйверов. б) Очень молодой
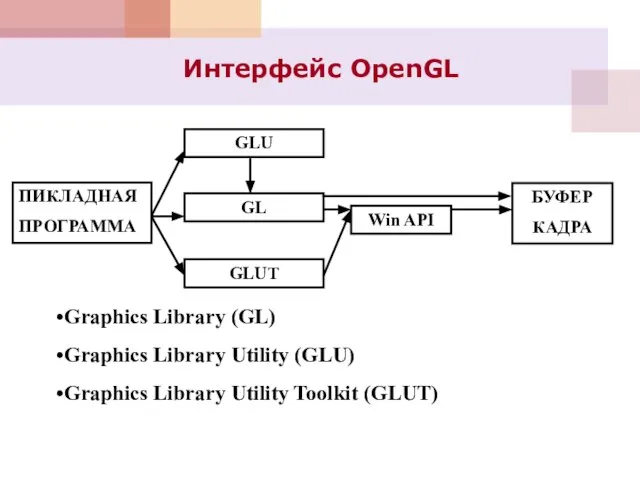
- 48. Интерфейс OpenGL Graphics Library (GL) Graphics Library Utility (GLU) Graphics Library Utility Toolkit (GLUT)
- 49. glBegin( ); // указываем тип примитива glVertex[2 3][ i f v](...); // первая вершина ……………………………// остальные
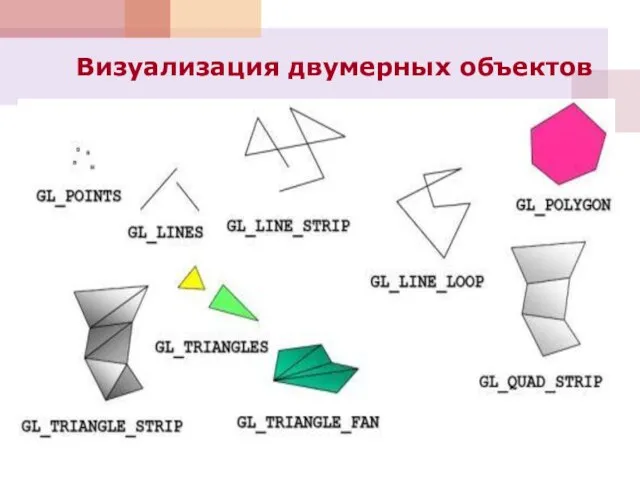
- 50. Визуализация двумерных объектов
- 51. Визуализация двумерных объектов
- 52. Визуализация двумерных объектов
- 53. Область вывода После применения матрицы проекций на вход следующего преобразования подаются усеченные координаты, для которых значения
- 54. МАТРИЦЫ OPENGL glMatrixMode(mode); Mode: Видовая: GL_MODELVIEW, Проекций: GL_PROJECTION, Tекстуры: GL_TEXTURE glLoadIdentity = glPushMatrix glPopMatrix
- 55. ПРЕОБРАЗОВАНИЯ OPENGL Масштабирование: glScale[2 3] [I f d] (α, β ,γ); α – относительно оси абсцисс,
- 56. TAO Tao Framework: OpenGL + C#
- 57. Установка Скачать Tao Framework можно с официальной страницы фреймворка на sourceforge.net: www.sourceforge.net/projects/taoframework Установка крайне проста, состоит
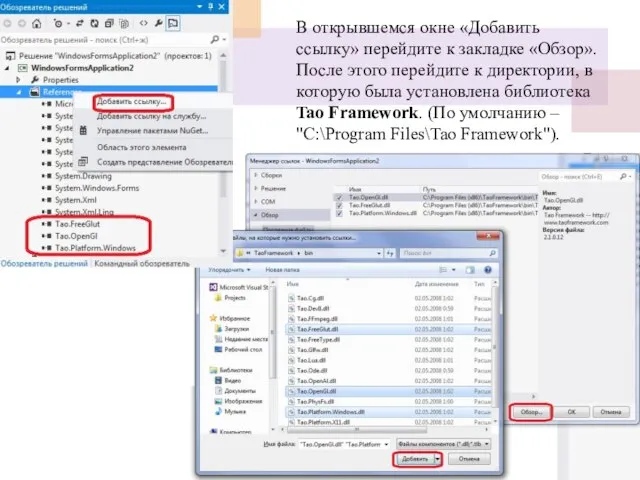
- 58. В открывшемся окне «Добавить ссылку» перейдите к закладке «Обзор». После этого перейдите к директории, в которую
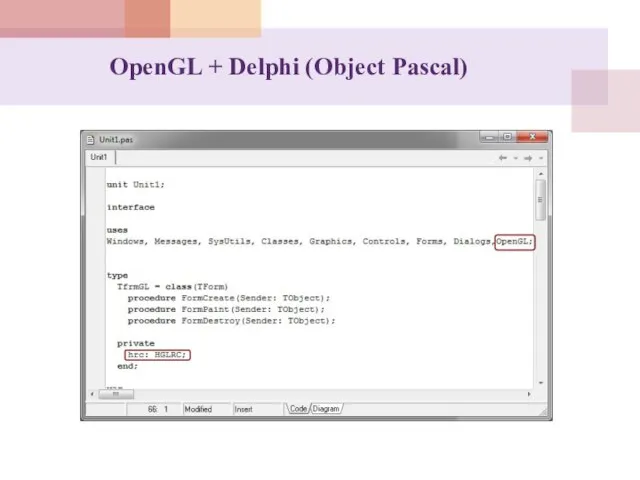
- 60. OpenGL + Delphi (Object Pascal)
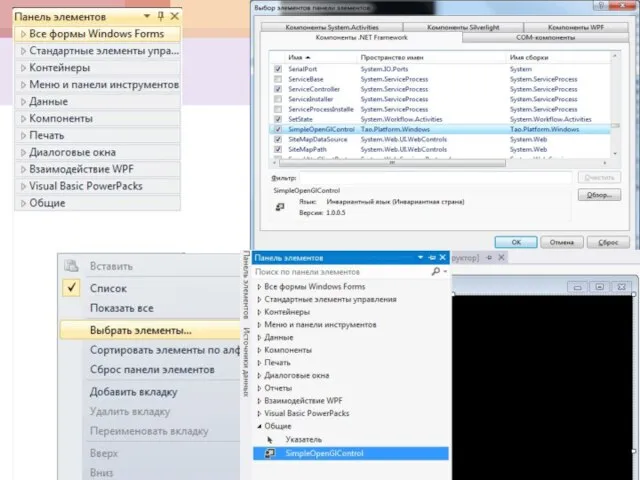
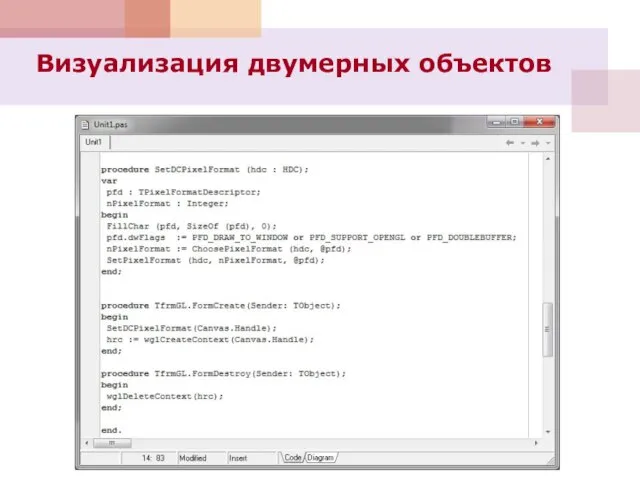
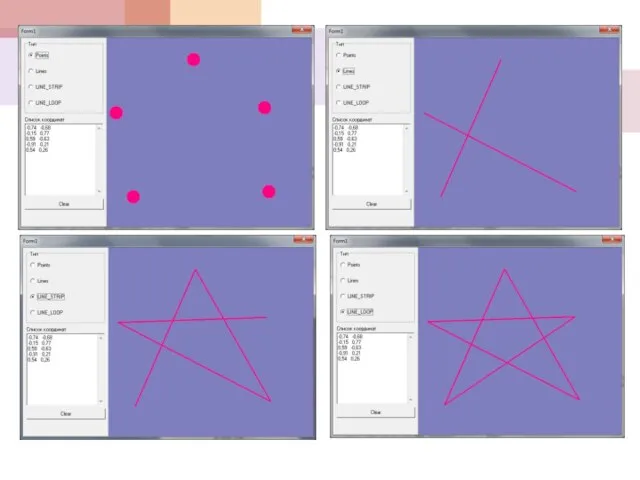
- 61. Визуализация двумерных объектов
- 62. Визуализация двумерных объектов
- 63. Визуализация двумерных объектов
- 64. Визуализация двумерных объектов
- 66. glPointSize (20); glColor3f (1.0, 1.0, 1.0); glBegin (GL_POINTS); glVertex2f (-1, -1); glVertex2f (-1, 1); glVertex2f (0,
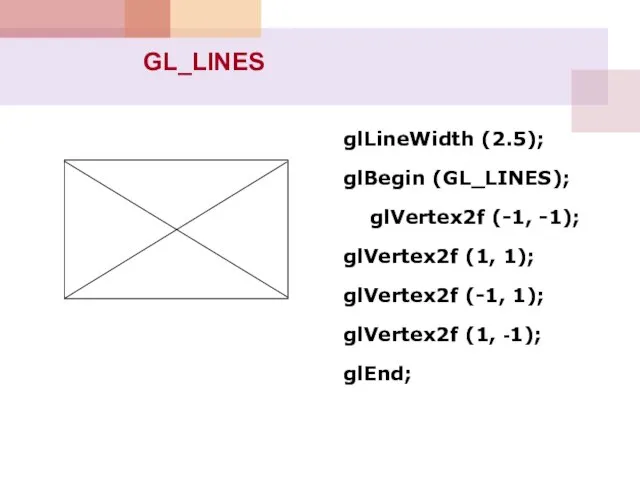
- 67. glLineWidth (2.5); glBegin (GL_LINES); glVertex2f (-1, -1); glVertex2f (1, 1); glVertex2f (-1, 1); glVertex2f (1, -1);
- 68. СОБЫТИЕ, СООБЩЕНИЕ, КОНТЕКСТ procedure TfmTest.Button1Click(Sender: TObject); var H : HWND; begin H := FindWindow('TForm1', 'Form1'); If
- 69. ССЫЛКИ НА КОНТЕКСТ УСТРОЙСТВА И ВОСПРОИЗВЕДЕНИЯ var dc : HDC; { ссылка на контекст устройства }
- 70. КОНТЕКСТ Приложению для того, чтобы воспользоваться функциями воспроизведения Windows, необходимо только указать ссылку на контекст устройства,
- 71. ФОРМАТ ПИКСЕЛЯ Прежде чем получить контекст воспроизведения, сервер OpenGL должен получить детальные характеристики используемого оборудования. Эти
- 72. Uses Windows, Messages, SysUtils, Classes, Graphics, Controls, Forms, Dialogs, OpenGL; ……. Private hrc: HGLRC; МИНИМАЛЬНАЯ ПРОГРАММА
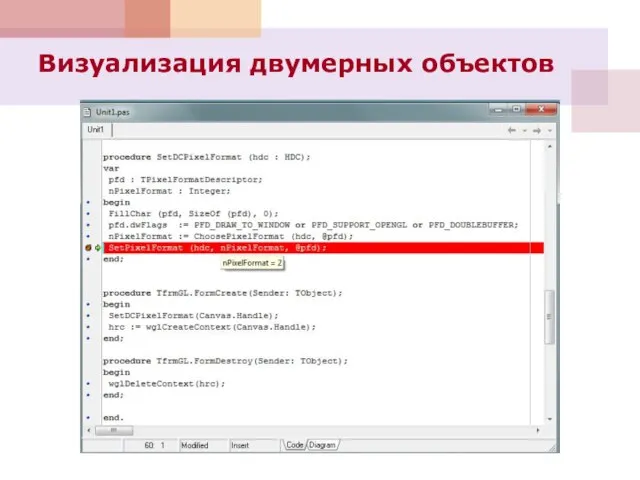
- 73. procedure SetDCPixelFormat (hdc : HDC); var pfd : TPixelFormatDescriptor; nPixelFormat : Integer; begin FillChar (pfd, SizeOf
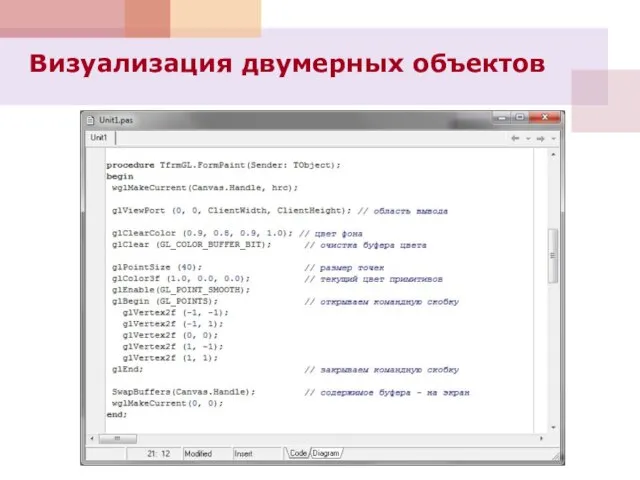
- 74. procedure TForm1.FormPaint(Sender: TObject); begin wglMakeCurrent(Canvas.Handle, hrc); // устанавливает текущий контекст воспроизведения glViewPort (0, 0, ClientWidth, ClientHeight);
- 75. procedure TfrmGL.FormCreate(Sender: TObject); begin SetDCPixelFormat(Canvas.Handle); hrc := wglCreateContext(Canvas.Handle); end; СОЗДАНИЕ ФОРМЫ
- 77. Скачать презентацию

















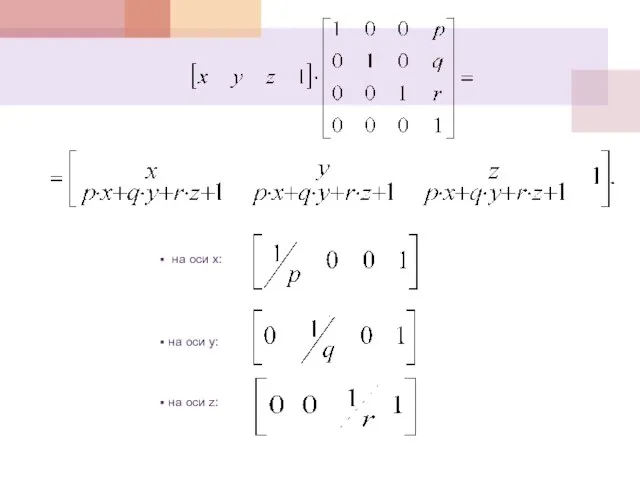







![glBegin( ); // указываем тип примитива glVertex[2 3][ i f v](...); //](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/878921/slide-48.jpg)




![ПРЕОБРАЗОВАНИЯ OPENGL Масштабирование: glScale[2 3] [I f d] (α, β ,γ); α](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/878921/slide-54.jpg)












 Двухсвязные списки
Двухсвязные списки Файлы и файловая система
Файлы и файловая система vis02
vis02 Контактный центр будущего
Контактный центр будущего ОП БД Лекция_1
ОП БД Лекция_1 Інформатика 9 клас. Урок 1
Інформатика 9 клас. Урок 1 Особенности репрезентации римской темы в российской социальной сети Вконтакте
Особенности репрезентации римской темы в российской социальной сети Вконтакте Электронные таблицы. Программы
Электронные таблицы. Программы Цифровые Двойники и Дата Майнинг
Цифровые Двойники и Дата Майнинг Original Character – Оригинальный Персонаж
Original Character – Оригинальный Персонаж Сайт almatygenplan.kz
Сайт almatygenplan.kz Макет здания
Макет здания Терминологический словарь по информатике
Терминологический словарь по информатике Siggraph. Graphics Gems for Games
Siggraph. Graphics Gems for Games Хранение информационных объектов различных видов на различных цифровых носителя
Хранение информационных объектов различных видов на различных цифровых носителя DeLion Steel. Проект
DeLion Steel. Проект Системы счисления
Системы счисления Территория самоуправления. Медиахолдинг в школе
Территория самоуправления. Медиахолдинг в школе Матрицы. 10 класс
Матрицы. 10 класс Программирование
Программирование Программирование на языке Паскаль
Программирование на языке Паскаль Простейший транзисторный мультивибратор
Простейший транзисторный мультивибратор Учебные исследовательские проекты на MS Excel. Построение и исследование функций одного аргумента
Учебные исследовательские проекты на MS Excel. Построение и исследование функций одного аргумента Образовательная платформа Ё-стади
Образовательная платформа Ё-стади Расчетные операции в Excel Работа с датами
Расчетные операции в Excel Работа с датами 2_3 OOP_C++
2_3 OOP_C++ Состав и работа ПК
Состав и работа ПК Создание графических изображений
Создание графических изображений