958092

Типы получения
Генераторы случайных чисел по способу получения чисел делятся на:
физические;
табличные;
алгоритмические.

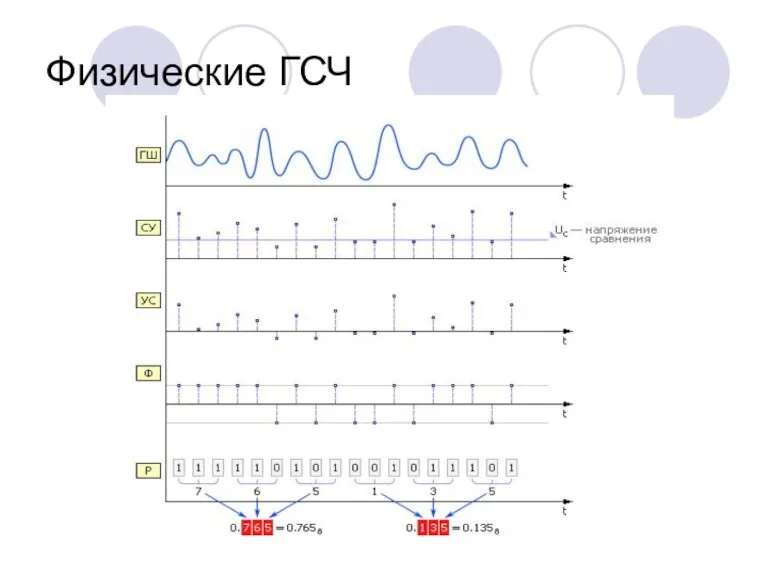
Физические ГСЧ

Табличные ГСЧ
Табличные ГСЧ в качестве источника случайных чисел используют специальным образом составленные таблицы, содержащие проверенные некоррелированные, то есть никак не зависящие друг от друга, цифры.

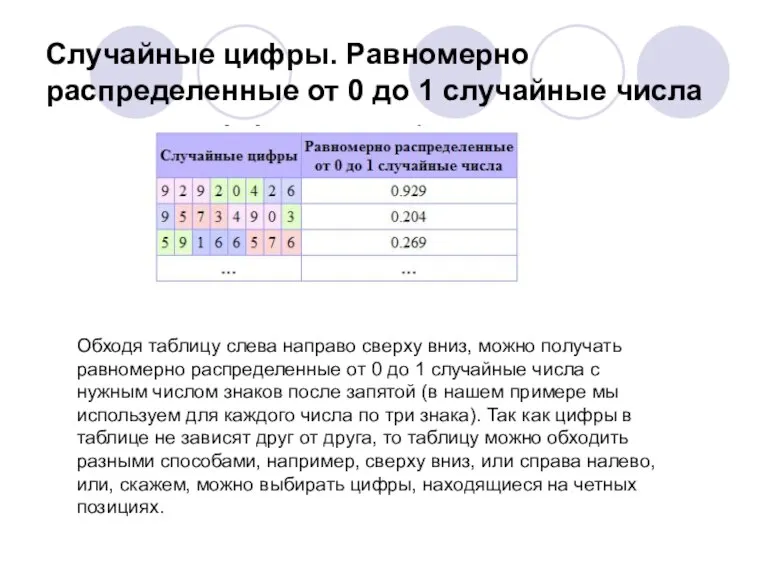
Случайные цифры. Равномерно
распределенные от 0 до 1 случайные числа
Обходя таблицу слева направо сверху вниз, можно получать равномерно распределенные от 0 до 1 случайные числа с нужным числом знаков после запятой (в нашем примере мы используем для каждого числа по три знака). Так как цифры в таблице не зависят друг от друга, то таблицу можно обходить разными способами, например, сверху вниз, или справа налево, или, скажем, можно выбирать цифры, находящиеся на четных позициях.

Табличные ГСЧ
Достоинство данного метода в том, что он дает действительно случайные числа, так как таблица содержит проверенные некоррелированные цифры.
Недостатки метода: для хранения большого количества цифр требуется много памяти; большие трудности порождения и проверки такого рода таблиц, повторы при использовании таблицы уже не гарантируют случайности числовой последовательности, а значит, и надежности результата.

Алгоритмические ГСЧ
Числа, генерируемые с помощью этих ГСЧ, всегда являются псевдослучайными (или квазислучайными), то есть каждое последующее сгенерированное число зависит от предыдущего:
r[i + 1] = f(r[i]).
Последовательности, составленные из таких чисел, образуют петли, то есть обязательно существует цикл, повторяющийся бесконечное число раз. Повторяющиеся циклы называются периодами.

Алгоритмические ГСЧ
Достоинством данных ГСЧ является быстродействие; генераторы практически не требуют ресурсов памяти, компактны.
Недостатки: числа нельзя в полной мере назвать случайными, поскольку между ними имеется зависимость, а также наличие периодов в последовательности квазислучайных чисел.

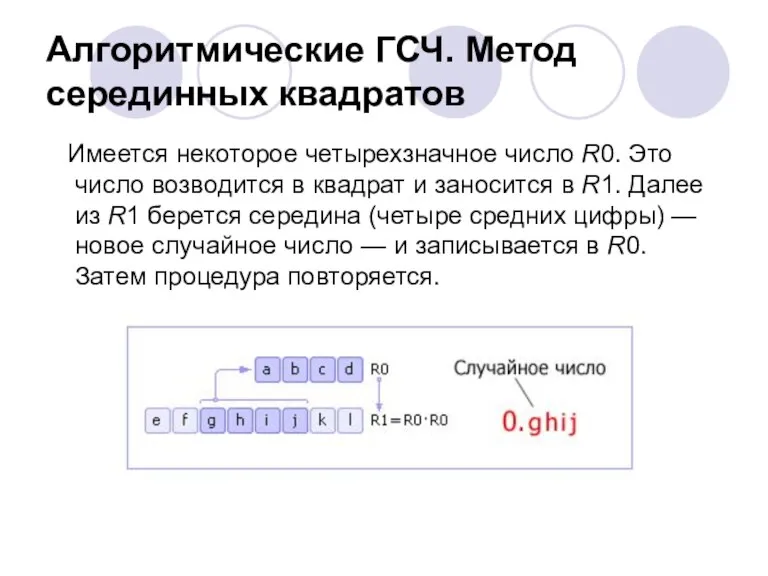
Алгоритмические ГСЧ. Метод серединных квадратов
Имеется некоторое четырехзначное число R0. Это число возводится в квадрат и заносится в R1. Далее из R1 берется середина (четыре средних цифры) — новое случайное число — и записывается в R0. Затем процедура повторяется.

Недостатки метода:
1) если на некоторой итерации число R0 станет равным нулю, то генератор вырождается, поэтому важен правильный выбор начального значения R0;
2) генератор будет повторять последовательность через Mn шагов (в лучшем случае), где n — разрядность числа R0, M — основание системы счисления.
Алгоритмические ГСЧ. Метод серединных квадратов

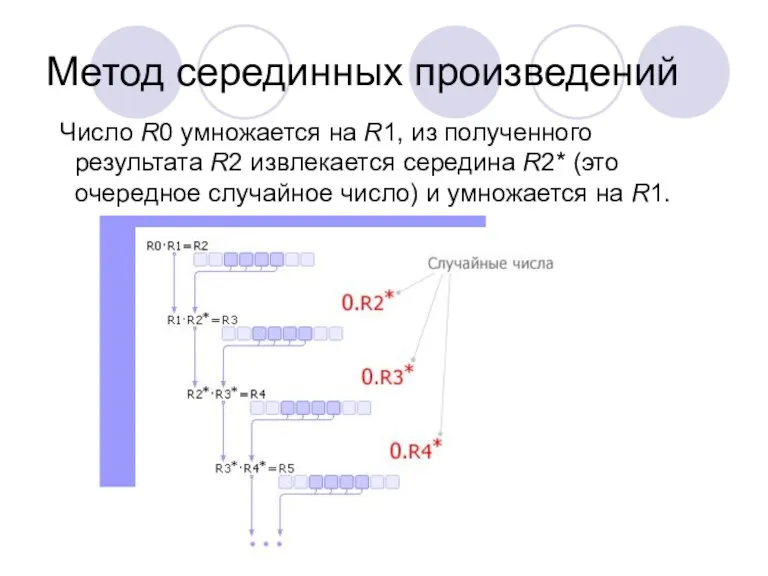
Метод серединных произведений
Число R0 умножается на R1, из полученного результата R2 извлекается середина R2* (это очередное случайное число) и умножается на R1.

Современные ГСЧ (криптографические)

Криптография и случайность имеют тесную связь
Совершенная секретность может быть достигнута, если ключ алгоритма шифровки - действительно случайное число.
Есть два подхода к получению длинного потока случайных битов.

Подходы к получению
Использование естественного случайного процесса, такого как многоразовое бросание монеты и интерпретация результата "орел" или "решка", как значения битов 0 или 1 .
Использование детерминированного процесса с информацией обратной связи.

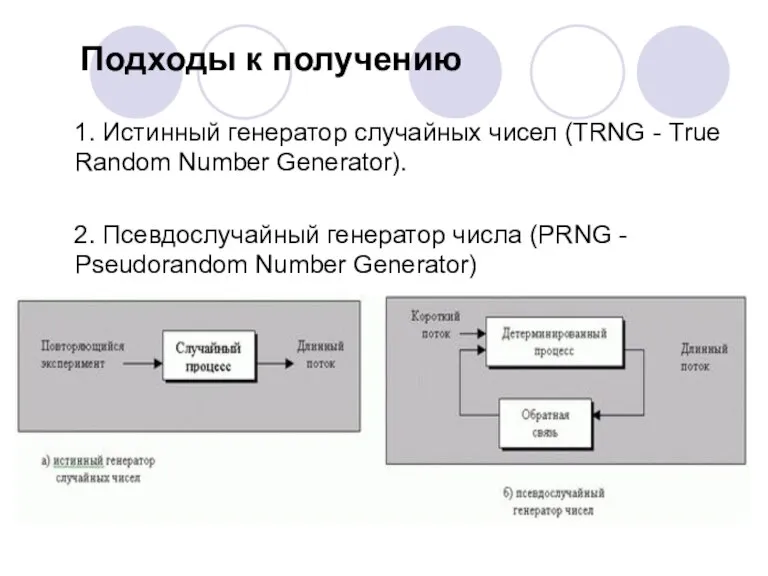
Подходы к получению
1. Истинный генератор случайных чисел (TRNG - True Random Number Generator).
2. Псевдослучайный генератор числа (PRNG - Pseudorandom Number Generator)

Истинный генератор случайных чисел (TRNG)
При бросании правильной монеты непрерывно возникает совершенный случайный поток битов, но это неприменимо на практике.
Естественные источники, которые могут произвести истинные случайные числа:
тепловой шум в электрическом резисторе
время ответа механического или электрического процесса после передачи команды.
Эти природные ресурсы использовались в прошлом, и некоторые из них были внедрены в коммерческую деятельность.
«-» Процесс обычно медленный
Один и тот же случайный поток не может быть повторен.

Генератор псевдослучайных чисел (PRNG)
Случайный поток битов может быть получен с использованием детерминированного процесса при введении короткого случайного потока (начального числа).
(Сгенерированное число не случайно, потому что процесс, который его создает, детерминирован).
Генераторы псевдослучайных чисел могут быть разделены на две широких категории:
конгруэнтные генераторы
генераторы, использующие криптографические шифры.

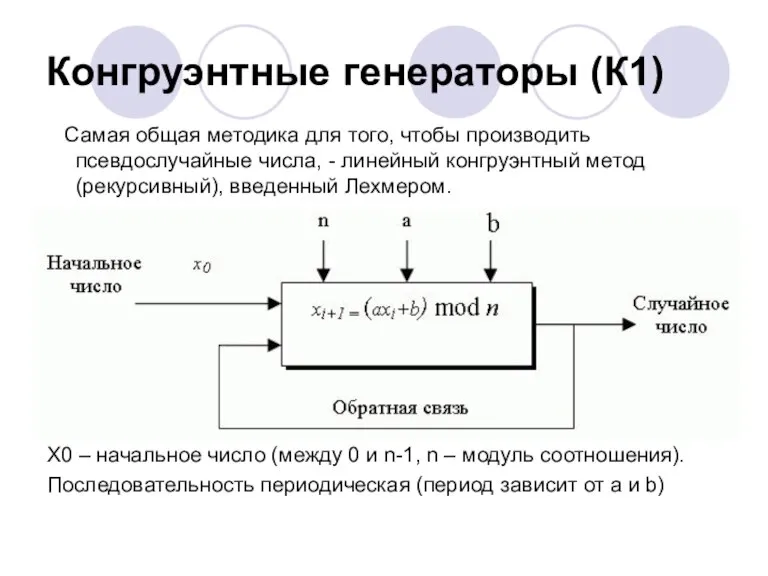
Конгруэнтные генераторы (К1)
Самая общая методика для того, чтобы производить псевдослучайные числа, - линейный конгруэнтный метод (рекурсивный), введенный Лехмером.
X0 – начальное число (между 0 и n-1, n – модуль соотношения).
Последовательность периодическая (период зависит от a и b)

Пример K.1
Предположим a = 4, b = 5, n = 17 и xi_0 = 7.
16, 1, 9, 7, 16, 1, 9, 7..., псевдослучайная последовательность с периодом 4.
Критерии. Для приемлемого генератора псевдослучайных чисел ( PRNG ) в течение прошлых нескольких десятилетий были разработаны несколько критериев.

Критерии
Период должен быть равен n (модулю). Это означает, что прежде чем целые числа в последовательности начинают повторяться, должны быть сгенерированы все целые числа между 0 и n - 1 .
Последовательность в каждый период должна быть случайна.
Процесс генерации должен быть удобен для реализации на компьютере. Большинство компьютеров сегодня эффективно, когда применяется арифметика, использующая слова по 32 бита.

Рекомендации
Рекомендуется выбрать коэффициенты конгруэнтного уравнения и значения модуля исходя из следующих соображений.
Оптимальный выбор модуля, n , - это наибольшее простое число, близкое к размеру слова, используемого в компьютере. Рекомендуется использовать тридцать первое простое число Мерсенны, как модуль:
n = M[31] = 2^31 - 1 .

Рекомендации
Чтобы создавать период, равный значению модуля, значение первого коэффициента a, должно быть первообразным корнем главного модуля (остаток от деления степени a). Хотя целое число 7 - первообразный корень M[31], рекомендуют использовать 7k, где k - целое число, взаимно-простое с ( M[31] - 1).
(Некоторые рекомендованные значения для k- это 5 и 13. (a = 7^5) или (a = 7^13)).
3. Для эффективного использования компьютера значение второго коэффициента b должно быть нулевым

Пример К1.
Линейный конгруэнтный генератор:
x[i+1] = ax[i] mod n, где n = 2^31 - 1
и a = 7^5 или a = 7^13

Безопасность
Последовательность, сгенерированная линейным конгруэнтным уравнением, показывает приемлемую случайность (если следовать предыдущим рекомендациям).
Последовательность полезна в некоторых приложениях, где требуется только случайность (таких как моделирование);
Последовательность бесполезна в криптографии, где желательны и случайность, и безопасность.

Безопасность
Поскольку число n общедоступно, последовательность может быть атакована с использованием одной из двух стратегий:
Если известно значение начального числа (x0) и коэффициент a;
Если не известно значение x0 и a, то можно перехватить первые два целых числа и использовать следующие два уравнения, чтобы найти x0 и a:
x[1] = ax[0] mod n
x[2] = ax[1] mod n

Генератор квадратичных вычетов
Чтобы получить менее предсказуемую псевдослучайную последовательность, был введен генератор квадратичных вычетов,
x[i+1] = x[i]^2 mod n,
где x[0] называют начальным числом, число между 0 и n -1.

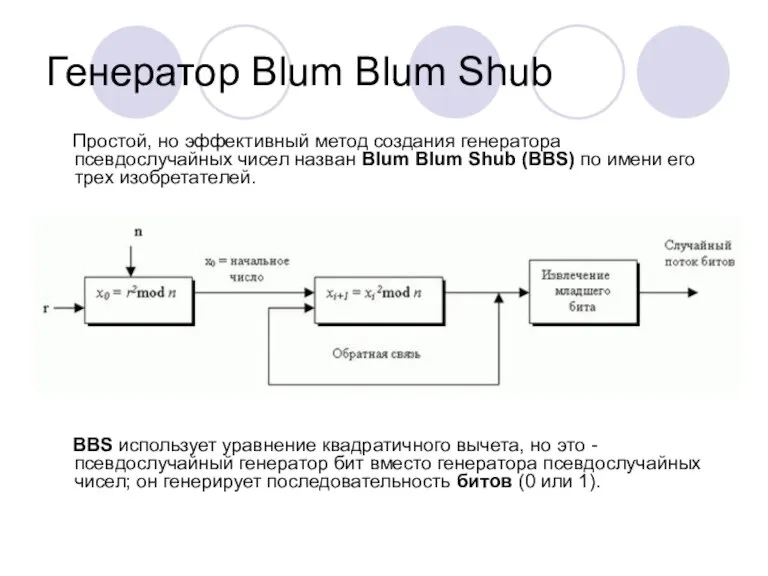
Генератор Blum Blum Shub
Простой, но эффективный метод создания генератора псевдослучайных чисел назван Blum Blum Shub (BBS) по имени его трех изобретателей.
BBS использует уравнение квадратичного вычета, но это - псевдослучайный генератор бит вместо генератора псевдослучайных чисел; он генерирует последовательность битов (0 или 1).

Генератор Blum Blum Shub.
Шаги генерации
Найдите два больших простых числа p и q в форме 4k + 3, где k - целое число ( p и q являются конгруэнтными 3 mod 4) .
Выберите модуль n = p × q .
Выберите случайное целое число r, которое является взаимно-простым с n.
Вычислите начальное число как x[0] = r^2 mod n .
Генерировать последовательность x[i+1[ = x[i]^2 mod n .
Взять самый младший бит сгенерированного случайного целого числа (LSB - Least Significant Bit) как случайный бит.

Безопасность
Может быть доказано, что если p и q известны, i -тый бит в последовательности может быть найден как самый младший бит:
X[i] = x[0]^(2^ i mod [(p-1)(q-1)])
Это означает, что если известно значение p и q, можно найти значение i-того бита, пробуя все возможные значения n (значение n обычно общедоступно). Тем самым сложность у этого генератора - та же самая, как у разложения на множители n .
Если n является достаточно большим, последовательность безопасна (непредсказуема). Было доказано, что при очень большом n невозможно предсказать значение следующего бита в последовательности, даже если знать значения всех предыдущих битов. Вероятность каждого принятия значений для каждого бита, 0 или 1, - очень близка к 50 процентам.
Безопасность BBS зависит от трудности разложения на множители n

Генераторы на основе криптографической системы
Криптографические системы, такие как шифр для процесса шифрования или хэш-функция, могут также быть использованы для генерации случайного потока битов. Можно выделить основные 2 системы, которые применяют алгоритмы шифрования.

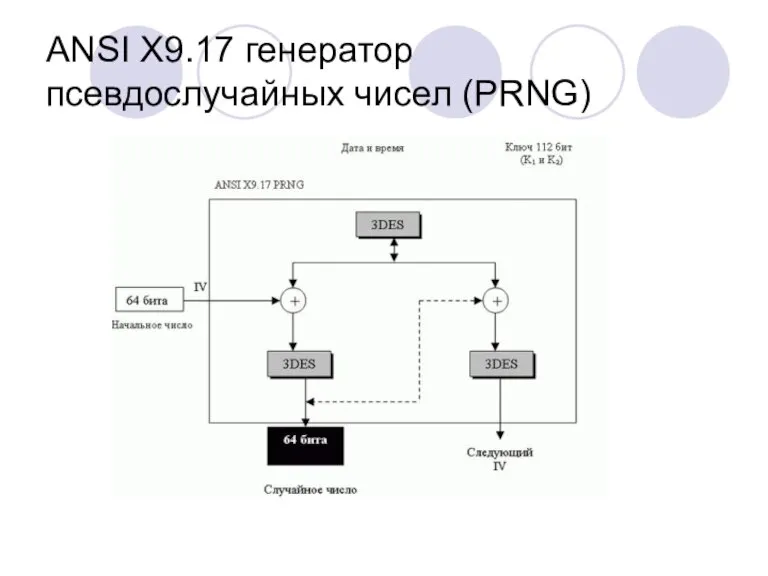
ANSI X9.17 генератор псевдослучайных чисел (PRNG)
ANSI X9.17 определяет криптографически сильный генератор псевдослучайных чисел, использующий тройной 3DES с двумя ключами (шифрация - дешифрация - шифрация).
Первое псевдослучайное число это 64-битовое начальное число, используемое как инициирующий вектор (IV);
остальная часть псевдослучайных чисел использует начальное число, показанное как следующие IV.
Тот же самый ключ засекречивания на 112 битов (K1 и K2 в 3DES) применяется для всех трех 3DES-шифров.

ANSI X9.17 генератор псевдослучайных чисел (PRNG)

Безопасность
Строгость X9.17 определяется следующими фактами:
Ключ - 112 (2 56) бит.
Ввод даты и времени на 64 бита обеспечивает хорошую метку времени, предотвращающую атаку воспроизведения.
Система обеспечивает превосходный эффект рассеивания и перемешивания с помощью шести шифрований и трех дешифрований.

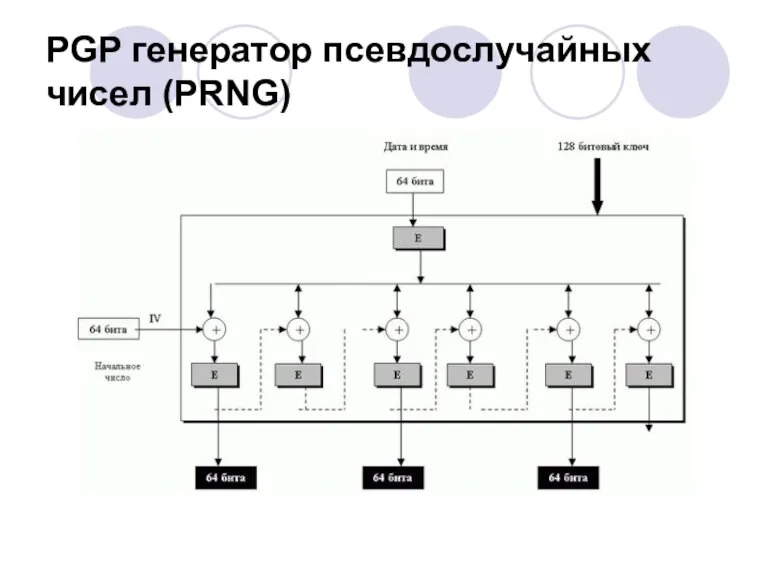
PGP генератор псевдослучайных чисел (PRNG)

Оператор RAND
i=rand(); - символьная константа, определенная в “stdlib.h”
0<=i<=MAX_RAND;
MAX_RAND>=32767.
Каждое число в этом диапазоне имеет «равные» шансы

Оператор RAND
Часто, диапазон необходимых значений не совпадает с диапазоном оператора (
подбрасывание монеты,
выбор значение на игральной кости)

Оператор RAND
Масштабирование случайной величины – сочетание с операцией rand операции «взятия по модулю»:
rand()%6;
Число 6 – коэффициент масштабирования.

Пример: бросание игральной кости
Моделируем процесс бросания игральной кости - 6000 раз. Тогда вероятность «выпадания» одного значения 1/6 при генерации случайной величины (события равновероятностны и равновозможны!).
1 значение – 1000 раз!

Пример: бросание игральной кости

«Крепс»