Алгебра логики

Высказывания
Алгебра логики – наука, изучающая законы и формы мышления; учение о способах рассуждений и доказательств.
Алгебра логики возникла в середине ХIХ века в трудах английского математика Джорджа Буля. Ее создание представляло собой попытку решать традиционные логические задачи алгебраическими методами.
Алгебра в широком смысле этого слова наука об общих операциях, аналогичных сложению и умножению, которые могут выполняться не только над числами, но и над другими математическими объектами.
Примеры алгебр: алгебра натуральных чисел, алгебра рациональных чисел, алгебра многочленов, алгебра векторов, алгебра матриц, алгебра множеств и т.д. Объектами алгебры логики или булевой алгебры являются высказывания.
Высказывание – это любое предложение какого-либо языка, в котором что-либо утверждается или отрицается. Любое высказывание можно определить как истинное или ложное (быть одновременно и тем и другим оно не может).
Пример: Определить значения истинности для следующих высказываний.
Лед – твердое состояние воды. Ответ: истинное высказывание.
Треугольник – это геометрическая фигура. Ответ: истинное высказывание.
Буква А – согласная. Ответ: ложное высказывание.

Высказывания (продолжение)
В естественном языке высказывания выражаются повествовательными предложениями. Восклицательные и вопросительные предложения высказываниями не являются.
Высказывания бывают общими, частными или единичными. Общее высказывание начинается (или может начать) со слов: все, всякий, каждый, ни один. Частное высказывание начинается (или может начать) со слов: некоторые, большинство и т.п. Во всех других случаях высказывание является единичным.
Пример.
Определить тип высказывания (общее, частное, единичное).
Все рыбы умеют плавать. Ответ: общее высказывание
Некоторые медведи - бурые. Ответ: частное высказывание
Париж – столица Китая. Ответ: единичное высказывание

Высказывания (продолжение)
Простые высказывания в алгебре логики обозначаются заглавными латинскими буквами.
Пример.
А = Число 8 кратно 4.
В = На яблонях растут бананы.
Истинному высказыванию ставится в соответствие 1, ложному – 0. Таким образом, А = 1, В = 0.
Буквы, обозначающие высказывания можно рассматривать как имена логических переменных. Логические переменные принимают два значения: 0 и 1 (на языке программирования: «ложь» - false, «истина» - true).

Высказывания (продолжение)
Высказывания могут выражаться с помощью математических, физических, химических и прочих знаков. Из двух числовых выражений можно составить высказывания, соединив их знаками равенства или неравенства.
Высказывание называется простым (элементарным), если никакая его часть сама не является высказыванием.
Примеры: Идет дождь. Нам живется весело. Число 8 кратно 2.
Выражение, состоящее из нескольких простых высказываний, называется составным (сложным). Простые высказывания соединяются с помощью логических операций (связок).
Употребляемые в обычной речи слова и словосочетания "не", "и", "или", "если... , то", "тогда и только тогда" и другие позволяют из уже заданных высказываний строить новые высказывания. Такие слова и словосочетания называются логическими связками.
Примеры: Идет дождь, а у меня нет зонта. Вася летом побывает и на море, и в горах. Число 8 кратно 2 и 4.

Самостоятельная работа №1 Высказывания.
1. Какие из предложений являются высказываниями? Определите их истинность.
Число 6 – четное.
Посмотрите на доску.
Все роботы являются машинами.
У каждой лошади есть хвост.
Кто отсутствует?
Х 2≥ 0
Выразите 1 час 15 минут в минутах.
2. Определите тип высказываний (общее, частное, единичное)
Все ананасы приятны на вкус.
Кошка является домашним животным.
Все лекарства неприятны на вкус.
Многие растения обладают целебными свойствами.
А – первая буква в алфавите.
Любой неразумный человек ходит на руках.
Мой кот страшный забияка.

Логические операции
Правила выполнения логических операций отражаются в таблицах, которые называются таблицами истинности.
Логическая операция – способ построения сложного
высказывания из простых высказываний,
при котором значение истинности сложного высказывания
полностью определяется значениями истинности простых высказываний.

Логическая операция КОНЪЮНКЦИЯ (лат. Conjunctio – связываю):
В естественном языке соответствует союзу И;
В математической логике обозначение: & , ∧ или • ;
В языках программирования: AND;
Иное название: логическое умножение.
Конъюнкция – двухместная операция; записывается в виде: А & В , A ∧ B, A • B. Значение такого выражения будет ЛОЖЬ, если хотя бы значение одного из высказываний ложно.
Пример.
1. А = На автостоянке стоит «Мерседес»
В = На автостоянке стоят «Жигули»
А & В = На автостоянке стоят «Мерседес» и «Жигули»
2. А = Число 6 делится на 3
В = Число 6 делится на 2
А & В = Число 6 делится на 3 и на 2

Логическая операция ДИЗЪЮНКЦИЯ
(лат. Disjunctio – различаю):
В естественном языке соответствует союзу ИЛИ;
В математической логике обозначение: ∨, +;
В языках программирования: OR;
Иное название: логическое сложение.
Дизъюнкция – двухместная операция; записывается в виде: А ∨ В. Значение такого выражения будет ИСТИНА, если хотя бы значение одного из высказываний истинно.
Пример.
1. А = На автостоянке стоит «Мерседес»
В = На автостоянке стоят «Жигули»
А ∨ В = На автостоянке стоит «Мерседес» или «Жигули»
2. А = Число 8 делится на 3
В = Число 8 делится на 2
А ∨ В = Число 8 делится на 3 или на 2

Логическая операция ИНВЕРСИЯ (лат. Inversio – переворачиваю):
В естественном языке соответствует частице НЕ;
В математической логике обозначение: ¬А или ;
В языках программирования: NOT;
Иное название: логическое отрицание.
Инверсия – унарная (одноместная) операция; записывается в виде: ¬А или .
Пример.
А = Я знаю китайский язык
= Я не знаю китайский язык
А = Число 8 делится на 2
= Число 8 не делится на 2

Логическая операция ИМПЛИКАЦИЯ (лат. Implicatio – тесно связываю):
В естественном языке соответствует обороту ЕСЛИ …, ТО …;
В математической логике обозначение: ⇒ или →;
Иное название: логическое следование.
Импликация – двухместная операция; записывается в виде: А ⇒ В. Значение такого выражения будет ЛОЖЬ тогда и только тогда, когда условие (первое высказывание) истинно, а следствие (второе высказывание) ложь.
Пример.
А = Выглянет солнце
В = Станет тепло
А ⇒ В = Если на улице солнце, то станет тепло
С = Станет холодно
А ⇒ С = Если на улице солнце, то станет холодно
В обычной речи связка “если ..., то” описывает причинно-следственную связь между высказываниями. Но в логических операциях смысл высказываний не учитывается. Рассматривается только их истинность или ложность. Поэтому не надо смущаться “бессмысленностью” импликаций, образованных высказываниями, совершенно не связанными по содержанию. Например, такими:
“если президент США — демократ, то в Африке водятся жирафы”,
"если арбуз — ягода, то в бензоколонке есть бензин”.

Логическая операция ЭКВИВАЛЕНТНОСТЬ
(лат. Aequivalens – равноценное):
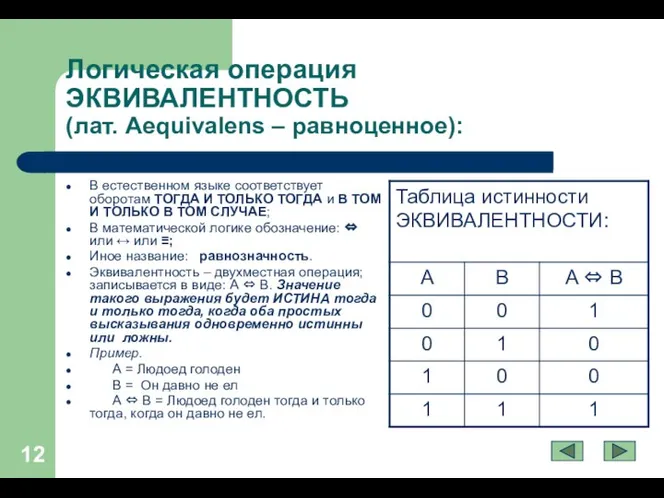
В естественном языке соответствует оборотам ТОГДА И ТОЛЬКО ТОГДА и В ТОМ И ТОЛЬКО В ТОМ СЛУЧАЕ;
В математической логике обозначение: ⇔ или ↔ или ≡;
Иное название: равнозначность.
Эквивалентность – двухместная операция; записывается в виде: А ⇔ В. Значение такого выражения будет ИСТИНА тогда и только тогда, когда оба простых высказывания одновременно истинны или ложны.
Пример.
А = Людоед голоден
В = Он давно не ел
А ⇔ В = Людоед голоден тогда и только тогда, когда он давно не ел.