Содержание
- 2. План урока:
- 3. Высказывание - это предложение на любом языке, содержание которого можно однозначно определить как истинное или ложное.
- 4. Наполеон был французским императором. Чему равно расстояние от Земли до Марса? Внимание! Посмотрите направо. Электрон –
- 5. Какие из приведенных примеров являются частными высказываниями, а какие общими? Не все книги содержат полезную информацию.
- 6. Для того, чтобы число делилось на 4, … чтобы оно было четным. Для того, чтобы число
- 7. Определение. Высказывание называется простым, если никакая его часть не является высказыванием. Употребляемые в обычной речи связки
- 8. Конъюнкция. Определение. Высказывание, составленное из двух и более высказываний путем объединения их связкой «И», называется конъюнкцией
- 9. Дизъюнкция. Определение. Высказывание, составленное из двух и более высказываний путем объединения их связкой «ИЛИ», называется дизъюнкцией
- 10. Исключающее ИЛИ. Определение. Высказывание, составленное из двух и более высказываний путем объединения их связкой «ЛИБО», называется
- 11. ИНВЕРСИЯ Определение. Отрицание (инверсия) – логическая операция, которая каждому элементарному высказыванию ставит в соответствие новое высказывание,
- 12. Правило построения отрицания к простому высказыванию: При построении отрицания к простому высказыванию либо используется речевой оборот
- 13. Задание. Постройте отрицание для высказываний: Все ребята умеют плавать. Невозможно создать вечный двигатель. Каждый человек –
- 14. . Приоритет операций. Каждое составное высказывание можно выразить в виде формулы (логического выражения), в которую войдут
- 15. Задания: 1. В следующих высказываниях выделите простые, обозначив каждое их них буквой; запишите с помощью букв
- 17. Скачать презентацию














 Разработка дополнительного программного модуля для конфигурации 1с предприятие
Разработка дополнительного программного модуля для конфигурации 1с предприятие Исследование методов и алгоритмов при решении задач об упаковке
Исследование методов и алгоритмов при решении задач об упаковке Личный кабинет ГИС ЖКХ
Личный кабинет ГИС ЖКХ Влияние информационной революции на Ж/Д отрасль
Влияние информационной революции на Ж/Д отрасль Гипертекст, гиперссылка
Гипертекст, гиперссылка Кружок Компьюша для детей 7-10 лет
Кружок Компьюша для детей 7-10 лет Первый баннер. ТЗ
Первый баннер. ТЗ Алгоритмизация и программирование. Язык C++
Алгоритмизация и программирование. Язык C++ Чемпионат CyberHeroes
Чемпионат CyberHeroes Комплексное тестирование и анкетирование
Комплексное тестирование и анкетирование Структура и уровни построения АСУ на транспорте, их функции, алгоритмы эффективного принятия оперативных решений
Структура и уровни построения АСУ на транспорте, их функции, алгоритмы эффективного принятия оперативных решений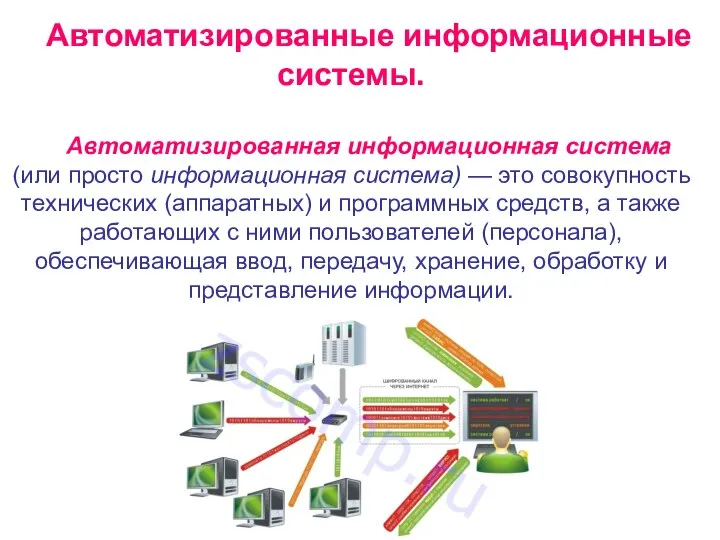 Автоматизированные информационные системы
Автоматизированные информационные системы Национальная Электронная Библиотека (НЭБ)
Национальная Электронная Библиотека (НЭБ) istoriya_razvitiya_vychislitelnoy_tehniki
istoriya_razvitiya_vychislitelnoy_tehniki Экзотика, эзотерика, перспективные направления. Лекция №9
Экзотика, эзотерика, перспективные направления. Лекция №9 Ввод и вывод. Паскаль. 8 класс
Ввод и вывод. Паскаль. 8 класс Korrekturen Email Client 2
Korrekturen Email Client 2 Аватарка как самоидентификация и самопрезентация
Аватарка как самоидентификация и самопрезентация Интегрированный урок информатики и литературы
Интегрированный урок информатики и литературы Метапредметный урок Система – это хаос или порядок? 5 класс
Метапредметный урок Система – это хаос или порядок? 5 класс Получение разрешения на добычу птицы в весенний сезон охоты
Получение разрешения на добычу птицы в весенний сезон охоты Фотография и компьютер. Документ или фальсификация: акт и его компьютерная трактовка
Фотография и компьютер. Документ или фальсификация: акт и его компьютерная трактовка Интернет-источники по географии
Интернет-источники по географии Применение формул для вычисления в таблицах, созданных в Microsoft Word 2007
Применение формул для вычисления в таблицах, созданных в Microsoft Word 2007 Опыт и результаты апробации инфраструктурных решений в рамках программы импортозамещения
Опыт и результаты апробации инфраструктурных решений в рамках программы импортозамещения Компьютерные технологии
Компьютерные технологии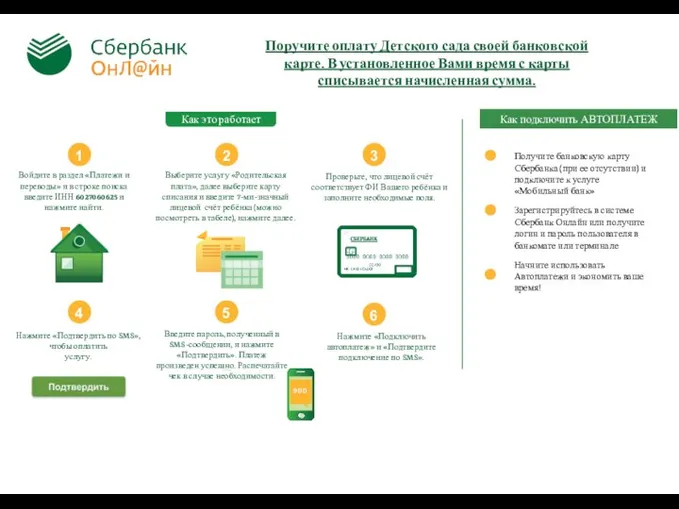 Оплата детского сада по банковской карте. Сбербанк ОнЛ@йн
Оплата детского сада по банковской карте. Сбербанк ОнЛ@йн Презентация на тему Алгоритм. Свойства алгоритма
Презентация на тему Алгоритм. Свойства алгоритма