Содержание
- 2. Independent and parallel visual processing of ensemble statistics: Evidence from dual tasks Vladislav Khvostov and Igor
- 3. An example
- 4. Greater or smaller than average?
- 5. Ensemble summary statistics The visual system can compute mean (Alvarez & Oliva, 2009), numerosity (Halberda, Sires,
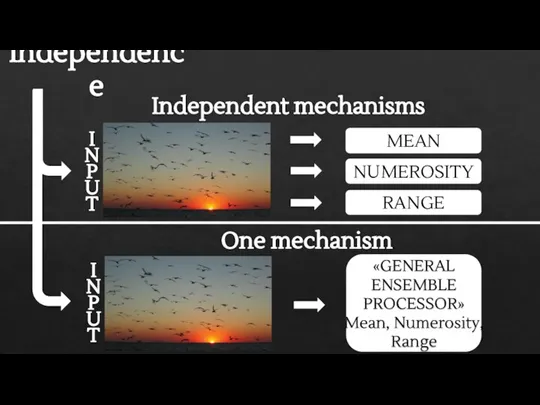
- 6. Independence
- 7. Correlational approach Prediction Independence
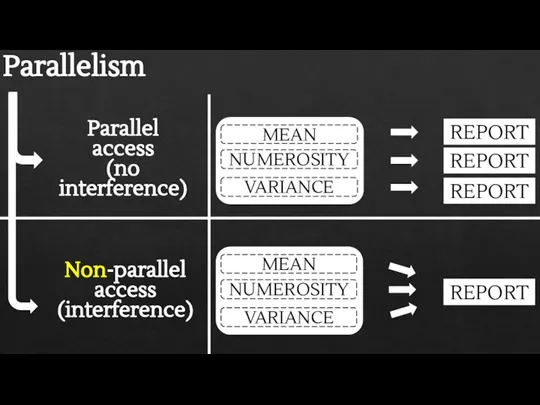
- 8. Parallelism Non-parallel access (interference)
- 9. Parallelism test Single task “Calculate MEAN” MEAN report Dual task Observers should compute only one statistics
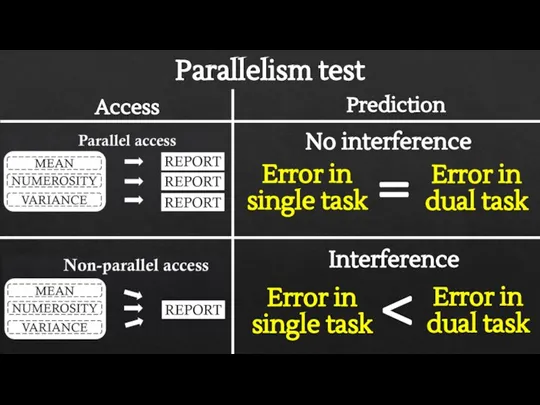
- 10. Parallelism test Prediction Access
- 11. Experiment 1 Whether mean and numerosity can be calculated independently and in parallel? N=23
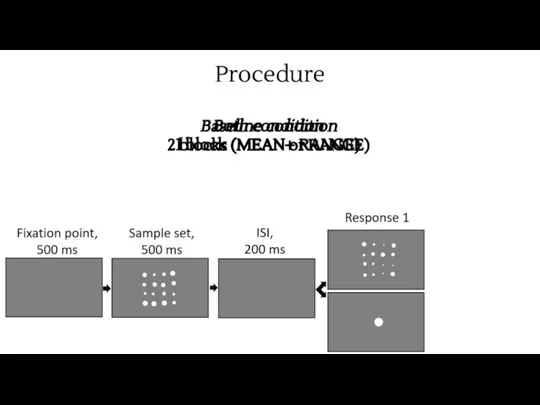
- 12. Procedure Baseline condition 2 blocks (MEAN or NUMEROSITY) Both condition 1 block (MEAN+ NUMEROSITY)
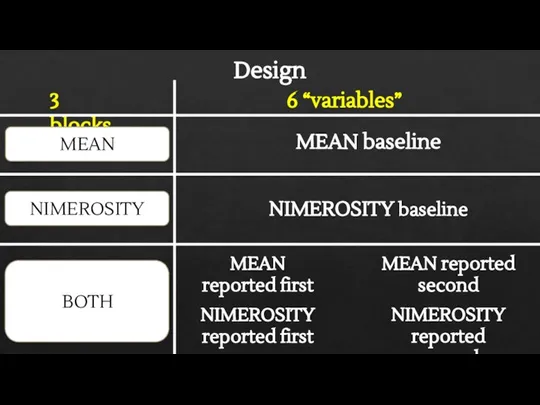
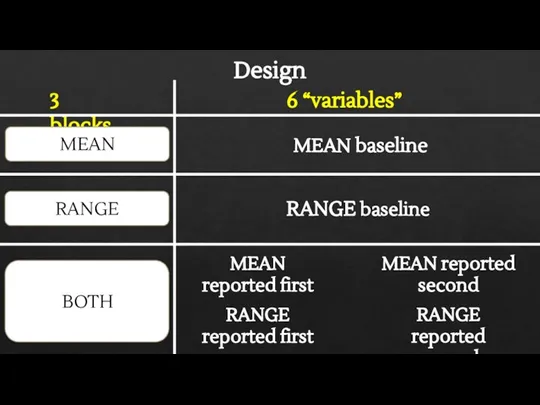
- 13. Design MEAN baseline 3 blocks MEAN NIMEROSITY BOTH 6 “variables” NIMEROSITY baseline MEAN reported first NIMEROSITY
- 14. Data analysis (1) Correlation between mean errors of 6 variables (across observers) (2) Trial-by-trial correlation between
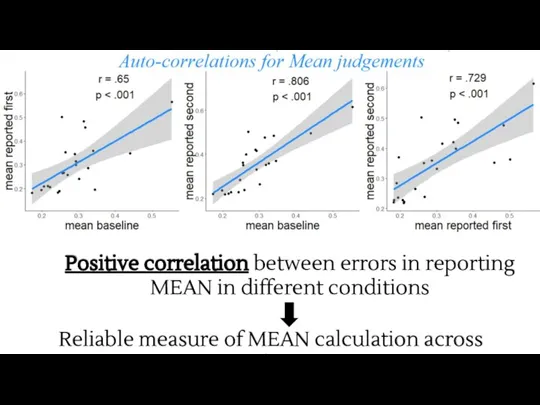
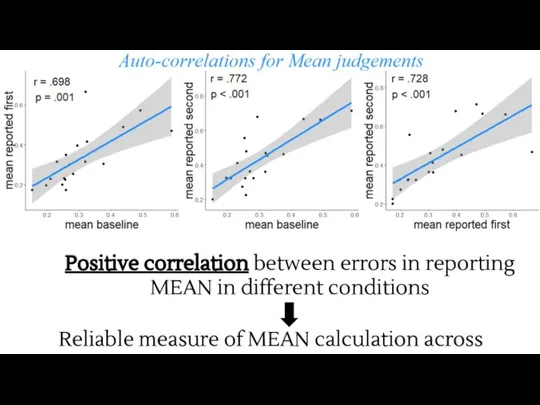
- 15. Positive correlation between errors in reporting MEAN in different conditions Reliable measure of MEAN calculation across
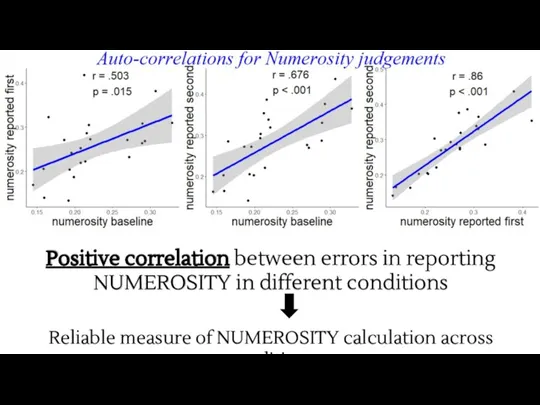
- 16. Positive correlation between errors in reporting NUMEROSITY in different conditions Reliable measure of NUMEROSITY calculation across
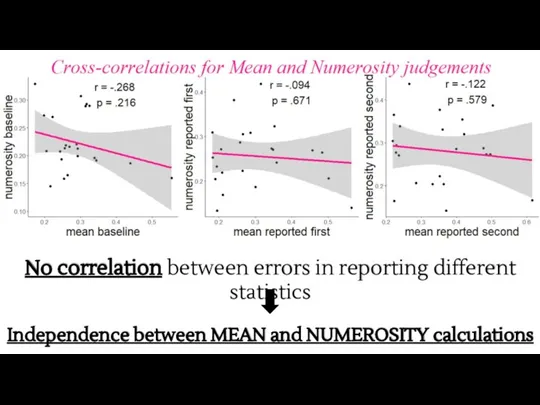
- 17. No correlation between errors in reporting different statistics Independence between MEAN and NUMEROSITY calculations
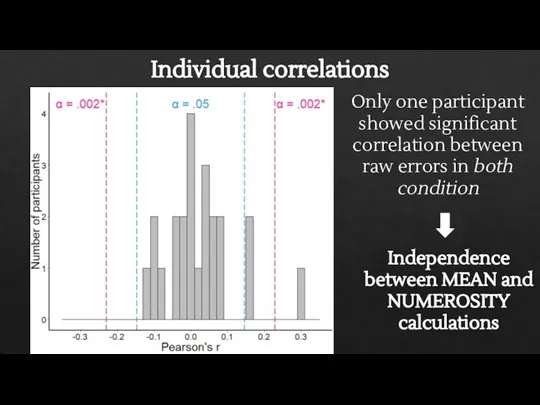
- 18. Individual correlations Only one participant showed significant correlation between raw errors in both condition Independence between
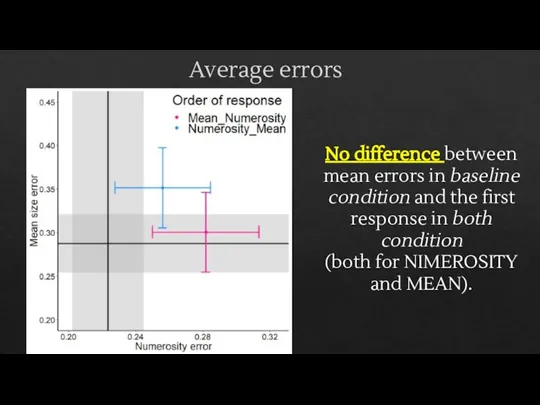
- 19. Average errors No difference between mean errors in baseline condition and the first response in both
- 20. Conclusion Mean and numerosity are calculated independently and in parallel
- 21. Experiment 2 Whether mean and range can be calculated independently and in parallel? N=20
- 22. Procedure Baseline condition 2 blocks (MEAN or RANGE) Both condition 1 block (MEAN+ RANGE)
- 23. Design MEAN baseline 3 blocks MEAN RANGE BOTH 6 “variables” RANGE baseline MEAN reported first RANGE
- 24. Positive correlation between errors in reporting MEAN in different conditions Reliable measure of MEAN calculation across
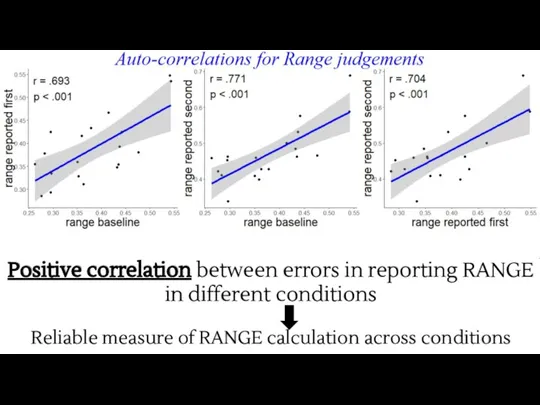
- 25. Positive correlation between errors in reporting RANGE in different conditions Reliable measure of RANGE calculation across
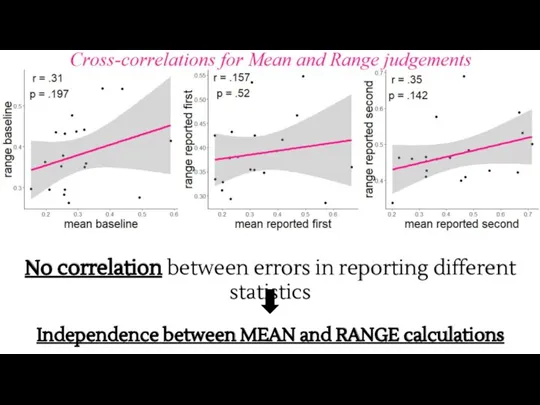
- 26. No correlation between errors in reporting different statistics Independence between MEAN and RANGE calculations
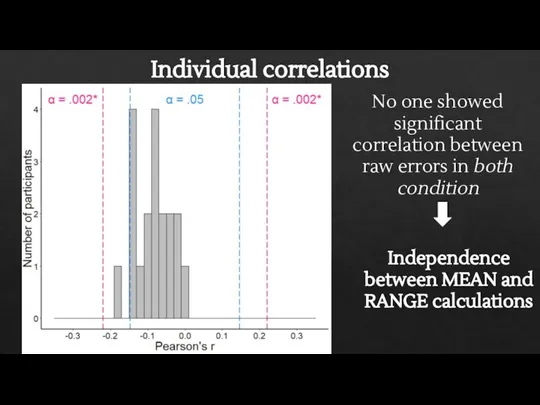
- 27. Individual correlations No one showed significant correlation between raw errors in both condition Independence between MEAN
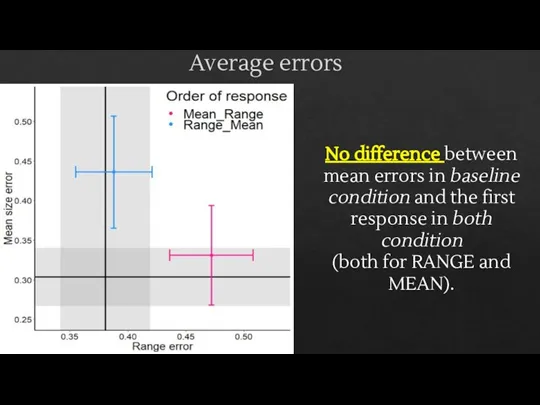
- 28. Average errors No difference between mean errors in baseline condition and the first response in both
- 29. Conclusions Ensemble summary statistics (mean and numerosity, mean and range) are calculated independently and in parallel
- 30. Conclusions (2) Independent calculation of ensemble summary statistics means: (1) Different summaries are calculated by different
- 31. For details and even one more experiment please read: Khvostov V.A., Utochkin I. S. Independent and
- 32. Thank you for being with me till the end of the first part
- 33. Confidence intervals in within-subject designs *Based on Cousineau, 2005 Part #2
- 34. It is all from this 4-pages paper
- 35. The problem Different subjects can perform very differently which increases a size of error bars Inconsistency
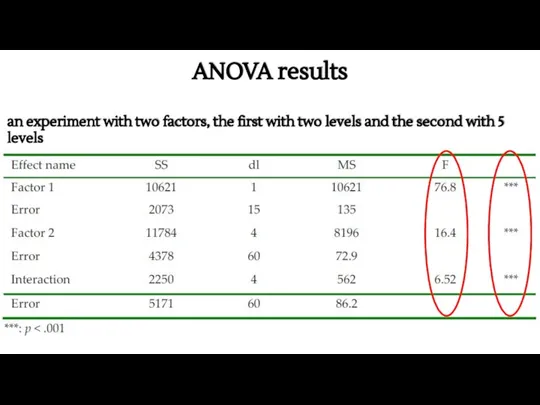
- 36. ANOVA results an experiment with two factors, the first with two levels and the second with
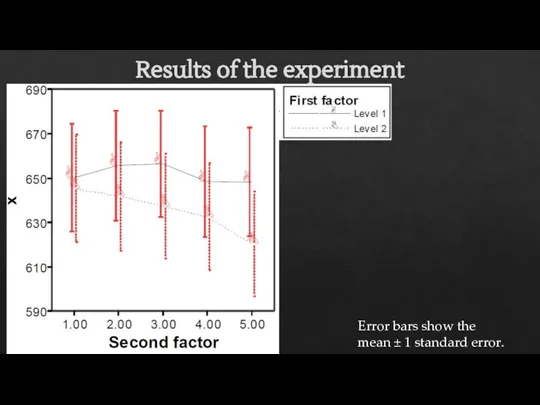
- 37. Results of the experiment Error bars show the mean ± 1 standard error.
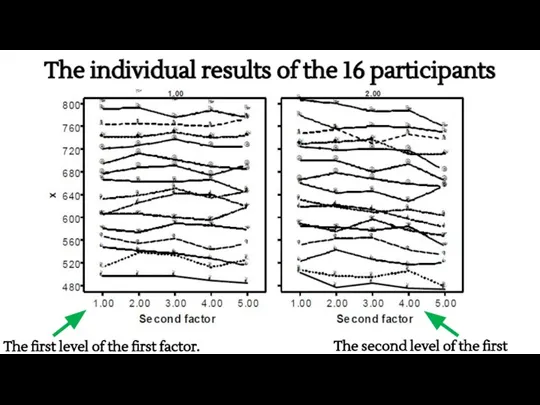
- 38. The individual results of the 16 participants The first level of the first factor. The second
- 39. The solution of the problem the participant mean Y = _ + the group mean results
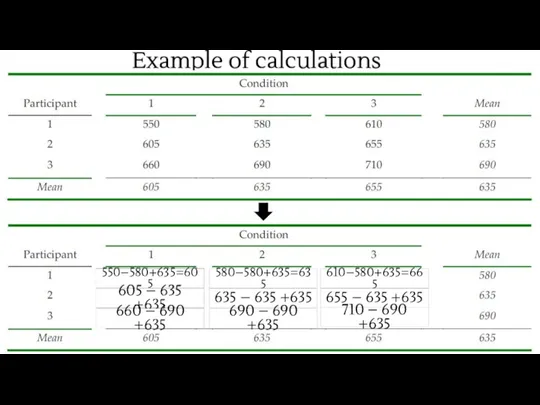
- 40. Example of calculations 550–580+635=605 580–580+635=635 610–580+635=665 605 – 635 +635 635 – 635 +635 655 –
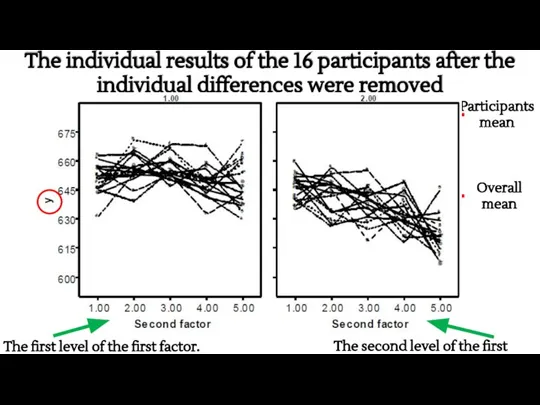
- 41. The individual results of the 16 participants after the individual differences were removed The first level
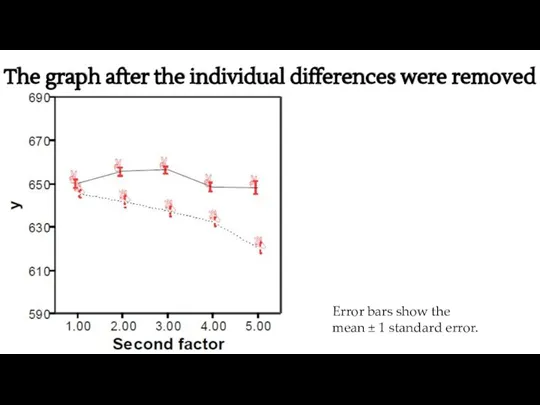
- 42. The graph after the individual differences were removed Error bars show the mean ± 1 standard
- 43. NOTE: Y is only useful for graphing purposes; for the analyses, continue to use the original
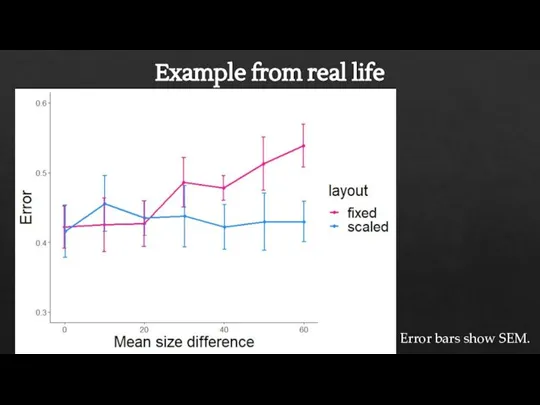
- 44. Example from real life Error bars show SEM.
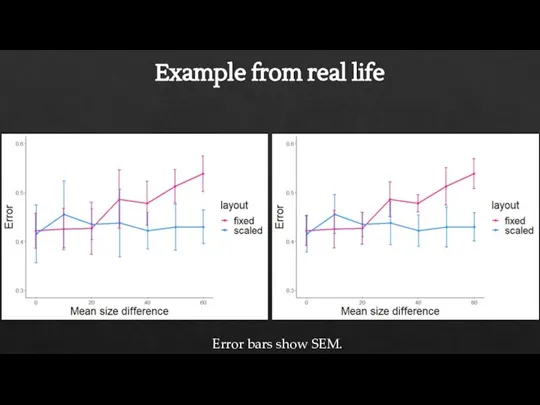
- 45. Example from real life Error bars show SEM.
- 47. Скачать презентацию




















 Функции JavaScript
Функции JavaScript Заказ данных спутников серии Landsat с сайта
Заказ данных спутников серии Landsat с сайта Установка Цифрового Сертификата YMCIS Ver
Установка Цифрового Сертификата YMCIS Ver Порядок действий при выводе на страницу данных из базы данных
Порядок действий при выводе на страницу данных из базы данных НДФЛ-практическая работа
НДФЛ-практическая работа Всемирная паутина
Всемирная паутина Связанные отношения
Связанные отношения Основы программирования на языке C++
Основы программирования на языке C++ Базы данных. § 12. Информационные системы
Базы данных. § 12. Информационные системы Информация и информационные процессы. Таблица степеней двойки
Информация и информационные процессы. Таблица степеней двойки Образец Защита проекта
Образец Защита проекта Формирование информационной грамотности через работу с текстом на уроках окружающего мира
Формирование информационной грамотности через работу с текстом на уроках окружающего мира Различные подходы к измерению количества информации
Различные подходы к измерению количества информации Презентация на тему Компьютерная графика
Презентация на тему Компьютерная графика  Динамические структуры данных (язык Си)
Динамические структуры данных (язык Си) Госуслуги для школьников
Госуслуги для школьников Информационная безопасность
Информационная безопасность Разработка приложения Test Creator
Разработка приложения Test Creator Метапредметный урок Система – это хаос или порядок? 5 класс
Метапредметный урок Система – это хаос или порядок? 5 класс КУРС Базовые приемы программирования. 2022. Онлайн - Лекция 2. Выполнение ЛР № 1. Списки.(2 поток)
КУРС Базовые приемы программирования. 2022. Онлайн - Лекция 2. Выполнение ЛР № 1. Списки.(2 поток) Основные компоненты компьютера и их функции. Устройство обработки информации - центральный процессор
Основные компоненты компьютера и их функции. Устройство обработки информации - центральный процессор Серия компьютерных игр Ведьмак
Серия компьютерных игр Ведьмак Поиск научной информации в системе Pubmed с использованием фильтров (на примере вирусной инфекции)
Поиск научной информации в системе Pubmed с использованием фильтров (на примере вирусной инфекции) Проект ITeam
Проект ITeam ATOM RPG — компьютерная игра
ATOM RPG — компьютерная игра Онлайн учебник по математике
Онлайн учебник по математике Геоинформационные ресурсы
Геоинформационные ресурсы Обмен значений численных переменных. Лабораторная работа 2
Обмен значений численных переменных. Лабораторная работа 2