Алгоритмы и структуры данных. Стеки и очереди

Определения
Массив - это однородный, упорядоченный структурированный тип данных с прямым доступом к элементам. Элементы массива объединяются общим именем и занимают в компьютере определенную конечную область памяти.
Стек –тип данных, представляющий собой список элементов, организованных по принципу LIFO (англ. last in — first out, «последним пришёл — первым вышел»).
Очередь – тип данных, для которых доступ к элементам организован по принципу «первый пришёл — первый вышел» (FIFO, англ. first in, first out).

Ограничение доступа
Массив – доступ к любому элементу
Стек, очередь – доступ только к одному элементу.
Интерфейс стеков, очередей проектируется с расчетом на поддержку ограничений доступа. Доступ к другим элементам (по крайней мере теоретически) запрещен.

Абстракция
Стеки, очереди являются более абстрактными сущностями, чем массивы и многие другие структуры данных. Они определяются, прежде всего, своим интерфейсом: набором разрешенных операций, которые могут выполняться с ними. Базовый механизм, используемый для их реализации, обычно остается невидимым для пользователя

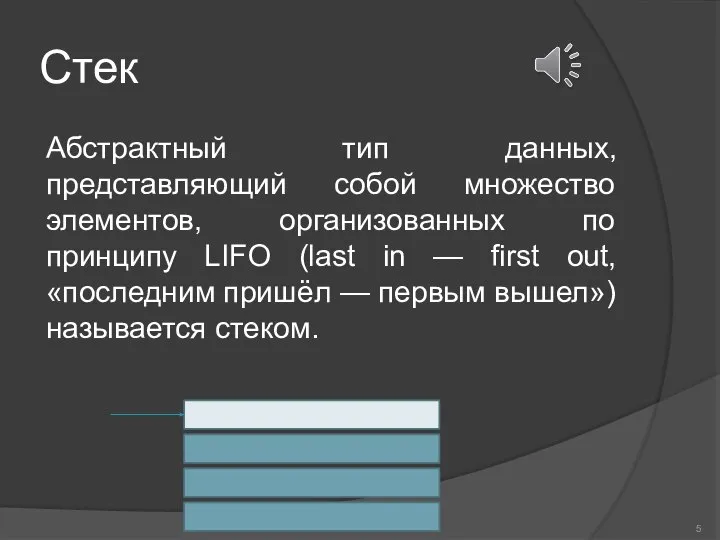
Стек
Абстрактный тип данных, представляющий собой множество элементов, организованных по принципу LIFO (last in — first out, «последним пришёл — первым вышел») называется стеком.

Основные методы работы со стеком
push – добавление нового элемента в стек
pop – извлечение элемента из вершины стека
peek – значение верхнего элемента
empty (new) – создание пустой структуры

Размер стека
Как правило, стек представляет собой небольшую структуру данных.
Размерность структуры определяется исходя из каких-то практических требований.

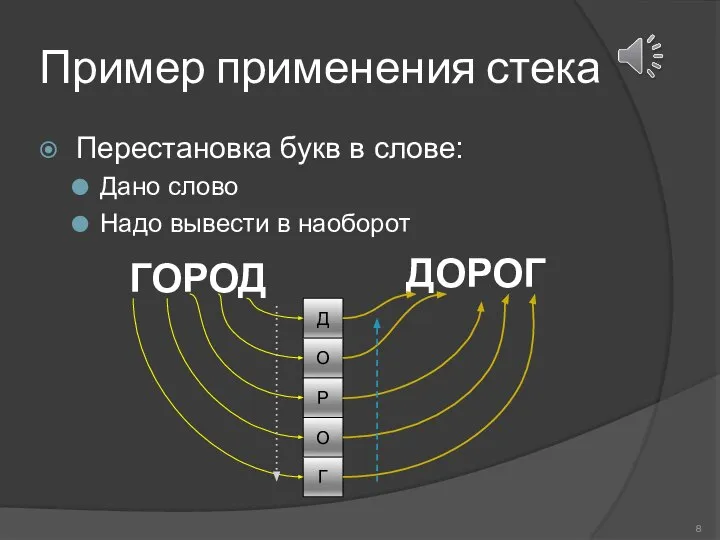
Пример применения стека
Перестановка букв в слове:
Дано слово
Надо вывести в наоборот
Г
О
Р
О
Д
ГОРОД
ДОРОГ

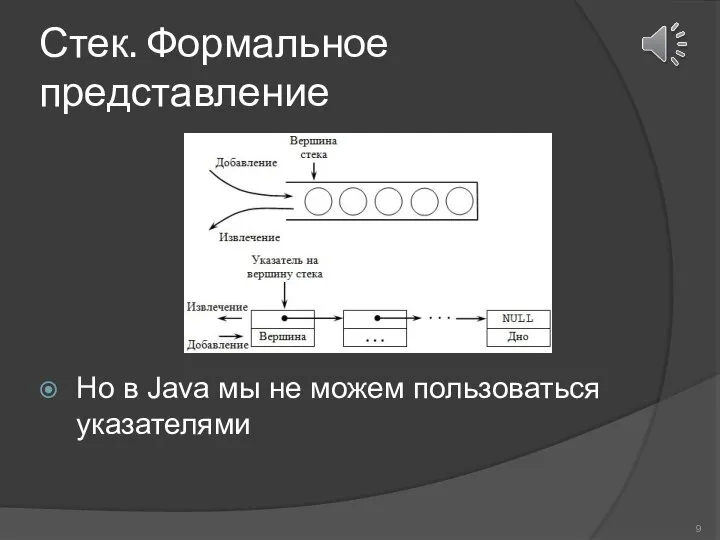
Стек. Формальное представление
Но в Java мы не можем пользоваться указателями

Реализация стека в Java
public StackX(int s) {
maxSize = s;
stackArray = new long[maxSize];
top = -1;}
public void push(long j) {
stackArray[++top] = j; }
public long pop(){
return stackArray[top--];
}

Реализация стека в Java (2)
public long peek(){
return stackArray[top];}
public boolean isEmpty(){
return (top == -1);}
public boolean isFull(){
return (top == maxSize-1);}

Обработка ошибок
if( !theStack.isFull() )
push(item);
else
System.out.print("Can't insert, stack is full");

Эффективность стеков
Занесение и извлечение элементов из стека выполняется за время O(1).
Иначе говоря, время выполнения операции не зависит от количества элементов в стеке. Следовательно, операция выполняется очень быстро,
не требуя ни сравнений, ни перемещений.

Очереди
Структура данных, называемая в информатике очередью, напоминает стек, но в очереди первым извлекается элемент, вставленный первым (FIFO, First-In-First-Out), тогда как в стеке, как мы видели, первым извлекается элемент, вставленный последним (LIFO).
*Изображение взято с сайта:
https://www.code-brew.com

Методы очереди
enqueue — добавление элемента в очередь;
dequeue — удаления элемента из очереди
new – создание пустой очереди
peek - получение элемента без удаления

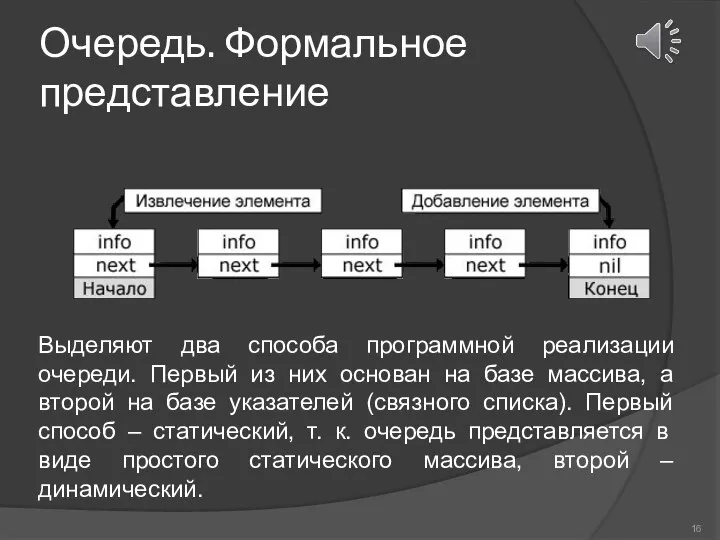
Очередь. Формальное представление
Выделяют два способа программной реализации очереди. Первый из них основан на базе массива, а второй на базе указателей (связного списка). Первый способ – статический, т. к. очередь представляется в виде простого статического массива, второй – динамический.

Реализация очереди в Java 1*
private int maxSize;
private long[] queArray;
private int front;
private int rear;
private int nItems;
public Queue(int s){
maxSize = s;
queArray = new long[maxSize];
front = 0;
rear = -1;
nItems = 0;}

Реализация очереди в Java 2*
public void insert(long j){
if(rear == maxSize-1)
rear = -1;
queArray[++rear] = j;
nItems++;}
public long remove(){
long temp = queArray[front++];
if(front == maxSize)
front = 0;
nItems--;
return temp;}

Реализация очереди в Java 3*
public long peekFront() {
return queArray[front];}
public boolean isEmpty(){
return (nItems==0);}
public boolean isFull() {
return (nItems==maxSize);}
public int size(){
return nItems;}

Реализация очереди без счетчика элементов 1*
private int maxSize;
private long[] queArray;
private int front;
private int rear;
public Queue(int s) {
maxSize = s+1;
queArray = new long[maxSize];
front = 0;
rear = -1;}

Реализация очереди без счетчика элементов 2*
public void insert(long j) {
if(rear == maxSize-1)
rear = -1;
queArray[++rear] = j;}
public long remove(){
long temp = queArray[front++];
if(front == maxSize)
front = 0;
return temp;}

Реализация очереди без счетчика элементов 3*
public long peek(){
return queArray[front];}
public boolean isEmpty(){
return ( rear+1==front || (front+maxSize-1==rear) );}
public boolean isFull() {
return ( rear+2==front || (front+maxSize-2==rear) )
}
public int size() {
if(rear >= front)
return rear-front+1;
else
return (maxSize-front) + (rear+1);}

Эффективность очередей
Вставка и извлечение элементов очереди, как и элементов стека, выполняются за время O(1).

Дек
Дек (deque) представляет собой двустороннюю очередь.
И вставка, и удаление элементов могут производиться с обоих концов.

Приоритетные очереди
Очередь с приоритетом (Priority queue) – очередь, в которой элементы имеют приоритет (вес)
Поддерживаемые операции:
Insert(key, value) – добавление элемента в очередь
DeleteMin/DeleteMax – удаляет из очереди элемент с мин./макс. ключом
Min/Max – возвращает элемент с мин./макс. ключом
DecreaseKey – изменяет значение ключа элемента
Merge(q1, q2) – сливает две очереди в одну

Структуры данных, лежащих в основе ПРИОРИТЕТНОЙ ОЧЕРДИ
Куча
Массив

Пример реализации 1* (на основе массива)
private int maxSize;
private long[] queArray;
private int nItems;
public PriorityQ(int s)
{maxSize = s;
queArray = new long[maxSize];
nItems = 0;}

Пример реализации 2*
public void insert(long item) {
int j;
if(nItems==0)
queArray[nItems++] = item;
else {
for(j=nItems-1; j>=0; j--) {
if( item > queArray[j] )
queArray[j+1] = queArray[j];
else
break; }
queArray[j+1] = item; // Вставка элемента
nItems++;
}}

Пример реализации 3*
public long remove()
{ return queArray[--nItems]; }
public long peekMin() {
return queArray[nItems-1]; }
public boolean isEmpty() { return (nItems==0); }
public boolean isFull()
{ return (nItems == maxSize); }