Архитектура и принципы работы эксперных систем

1.4 МАШИНА ВЫВОДА
Задача машины вывода состоит в “извлечении” ответа на вопрос задачи. Очевидно, для различных моделей знаний требуются различные машины вывода. Так, логическая машина вывода должна строить доказательства (теорем существования решений, например). Следует иметь в виду, что для неклассических логик, к которым относятся, например, нечеткая логика или многозначные логики, требуется строить собственную машину вывода, учитывающую специфику исчисления.
Машина вывода для продукционной базы знаний является интерпретатором правил, который использует факты, содержащиеся в базе знаний. На входе машина вывода получает цель консультации.
Машина вывода для табличной базы знаний часто основывается на использовании теоремы Байеса, но может использовать механизм классифицирующего дерева, дискриминантных функций, таблиц решений и поиска по образцу.

1.4 МАШИНА ВЫВОДА
Байесовский подход играет существенную роль при создании и использовании экспертных систем, использующих базу данных о предметной области, составленную по результатам наблюдений или экспериментов.
Основу байесовского подхода составляют следующие теоретические соотношения (на примере задачи медицинской диагностики).
Пусть необходимо производить диагностику между заболеваниями D1 , D2,…, Dn . Для каждого из этих заболеваний известны условные вероятности , характеризующие появление набора симптомов S при заболевании Dj. Здесь S = { S1 , S2 ,…, Sk } и Sk - различные симптомы. Пусть далее P(Dm) − априорная вероятность заболевания Dm. Тогда задача дифференциальной диагностики может быть сведена к статистической задаче выбора гипотез, решение которой основывается на использовании теоремы Байеса:
(4.1)

1.4 МАШИНА ВЫВОДА
Так же для поиска решения в условиях неопределенности большую роль играет теорема Байеса. Эта теорема позволяет оценить вероятность гипотезы при наличии одного или нескольких дополнительных признаков. Та гипотеза, вероятность которой оказывается наибольшей, и принимается в качестве рабочей.
Теорема Байеса имеет важное диагностическое значение и позволяет оценить вероятность гипотезы при наличии свидетельств.
Пусть даны следующие данные:

1.4 МАШИНА ВЫВОДА

1.4 МАШИНА ВЫВОДА
В этой таблице разумно увязать колонку Оборот с гипотезами. Имеется три гипотезы: Оборот = низкий, Оборот = средний, Оборот = высокий. На вероятность оборота влияют два показателя: жанр и цена. Сначала приведем формулу Байеса для случая одного свидетельства:
4.2

1.4 МАШИНА ВЫВОДА
В (4.2) − это гипотезы, причем они должны образовывать полную группу гипотез (других гипотез теоретически быть не должно или исследователь считает, что таковых нет); E – это свидетельство. Обозначение определяет вероятность свидетельства Е при справедливости гипотезы
Пример,
=0.2 (1 случа из пяти, когда был зафиксирован низкий оборот).
Таким образом, найдем

1.4 МАШИНА ВЫВОДА
Непосредственные расчеты дают
Далее найдем:
и

1.4 МАШИНА ВЫВОДА
Теперь ясно, что при выпуске книги по программированию на основании данных приведенной выше таблицы следует рассматривать средний оборот как наиболее вероятный.
При наличии двух и более свидетельств формула Байеса усложняется с учетом зависимости между свидетельствами. Поэтому мы дадим ее вариант только в предположении, что свидетельства независимы. Это, на самом деле, не столь ошибочное допущение, как может показаться, поскольку более важно выполнить сравнительное сопоставление альтернатив, а не их точное измерение. Так, для двух свидетельств имеем:

1.4 МАШИНА ВЫВОДА
Для большего числа свидетельств все получается по аналогии.
В ЭС формула Байеса может применяться для оценки вероятностей заключений продукционных правил на основе данных о достоверности их посылок. Заключения (выводы) в этом случае соответствуют гипотезам в теореме Байеса, а посылки − свидетельствам. Обычно посылка правила в ЭС содержит несколько условий. Вероятности P(Hi) и P(E/Hi) определяются на основе статистических данных с использованием формул теории вероятностей.
Основные из этих формул следующие.
Формула умножения вероятностей (вероятность того, что произойдет и событие A, и событие B):
P(A и B) = P(A) ⋅P(B/A) = P(B) ⋅P(A/B),

1.4 МАШИНА ВЫВОДА
где P(A), P(B) - вероятности событий A и B;
P(B/A) - условная вероятность события B, т.е. вероятность события B при условии, что произошло событие A;
P(A/B) - условная вероятность события A, т.е. вероятность события A при условии, что произошло событие B.
Если события A и B независимы (т.е. вероятность одного события не зависит от того, произошло ли другое событие), то формула умножения вероятностей записывается следующим образом: P(A и B) = P(A)⋅P(B).
Формула умножения вероятностей для нескольких событий
(вероятность того, что произойдут все указанные события вместе):
P(A1 и A2 и ... и An) = P(A1) ⋅ P(A2/A1) ⋅ P(A3/A1,A2) ... ⋅ P(An/A1,A2,..., An-1).

1.4 МАШИНА ВЫВОДА
Формула сложения вероятностей (вероятность того, что произойдет
хотя бы одно из событий):
P(A+B) = P(A) + P(B) - P(A и B).
Если события A и B несовместны (т.е. не могут произойти вместе),
то P(A и B)=0, и формула сложения вероятностей принимает следующий вид:
P(A+B) = P(A) + P(B).

1.4 МАШИНА ВЫВОДА
Если события A и B несовместны (т.е. не могут произойти вместе), то P(A и B)=0, и формула сложения вероятностей принимает следующий вид:
P(A+B) = P(A) + P(B).
Формула сложения вероятностей для нескольких событий обычно записывается следующим образом:
P(A1 + A2 + ... + An ) = 1 − P(A1)+ P(A2) + ... + P(An ) ,
где P(A1 + A2 + ... + An ) - вероятность того, что произойдет хотя бы одно из событий A1, A2,...An.
Если события образуют полную группу, то
Из теоремы следует формула вероятности для противоположного события

1.4 МАШИНА ВЫВОДА
Машина вывода может использовать механизм эвристического поиска на дереве состояний задачи (которое называют также деревом решения). Рассмотрим пятерку:
, (4.2)
где S0 - исходное состояние системы (объекта, модели); SF - конечное (искомое) состояние системы (объекта, модели); A - алгоритм отображения A: S0 → SF .
Определение 1.9. Состояние Si , непосредственно достижимое из состояния Sk, называется преемником Sk, а Sk – предшественником Si .
Определение 1.10. Граф Г(S, π) с множеством вершин-состояний Sj ∈ S и дуг π, связывающих предшественников и преемников, образует дерево решения с корнем S0 и листом SF , если:
μ-й ярус в Г образуют те преемники (μ-1)-го яруса (μ =1,2,…), которые не входят в ярусы (μ-2), (μ-3) и т.д.
листьями в Г являются состояния, все преемники которых содержатся в верхних ярусах (за исключением SF ).

1.4 МАШИНА ВЫВОДА
Задача машины вывода состоит в отыскании пути (как правило, кратчайшего) из S0 в SF . Любая часть этого пути называется трассой вывода. Для построения трассы вывода на дереве задачи используют механизм оценочных эвристических функций. Примером подобного эвристического алгоритма является алгоритм A* Нильссона. Качество эвристических оценочных функций определяется тем, насколько близко создаваемая алгоритмом трасса вывода “держится” к оптимальной; можно использовать, например, такую оценку:
K=L/T. (4.3)
Здесь Т − общее число вершин, пройденных в дереве решения; L – длина оптимального пути из S0 в SF.

1.4 МАШИНА ВЫВОДА
Достаточно часто машина вывода реализуется как совместная человеко-машинная подсистема, где в процессе поиска решения участвует человек.
Решение задач (из различных областей) является важнейшей стороной человеческой деятельности. Проблема автоматизации этого процесса критична для исследователей, алгоритмистов, математиков и инженерно-научных работников.
Парадигма человеко-машинной решающей системы (ЧМРС) состоит в том, что человек-решатель ищет решение задачи, создавая дерево контекстов с корневым контекстом , представляющим исходную спецификацию задачи. Каждый контекст представляет некую i-ую модель задачи, которая в формальном плане является расширением . Переход от одного контекста к его дочерним контекстам является результатом построения гипотез.

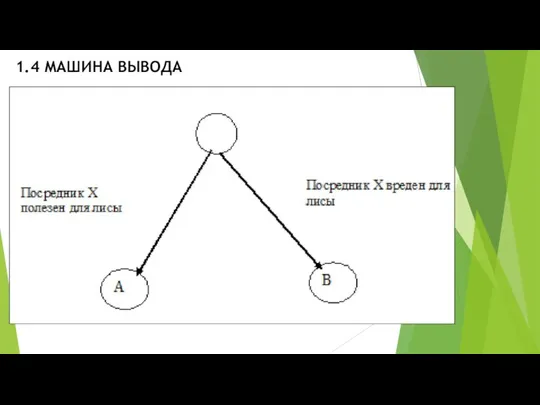
1.4 МАШИНА ВЫВОДА
Пример.
Почему лиса берет в пасть пучок травы, заплывает на середину реки и отпускает пучок по течению?
Сначала сформулируем готовый ответ. Ищем посредника между лисой и пучком травы. Этот посредник удаляется вместе с пучком. Значит, лисе он нежелателен. От него лисе вред. Вывод: посредник – насекомые.
Важным моментом в решении этой и других задач является использование гипотез. Строится дерево гипотез, которое помогает найти решение. Дерево гипотез – важнейший механизм поиска, позволяющий приблизиться к ответу. Начнем строить такое дерево, например, таким образом:

1.4 МАШИНА ВЫВОДА

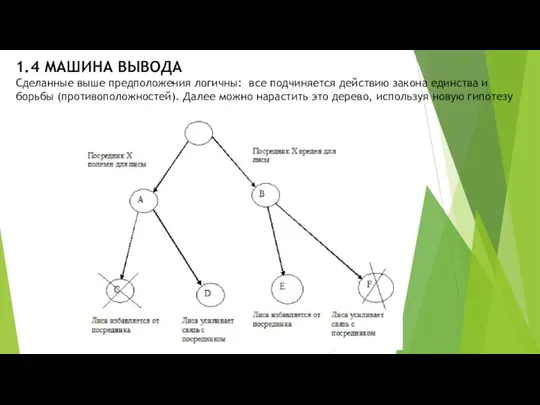
1.4 МАШИНА ВЫВОДА
Сделанные выше предположения логичны: все подчиняется действию закона единства и борьбы (противоположностей). Далее можно нарастить это дерево, используя новую гипотезу

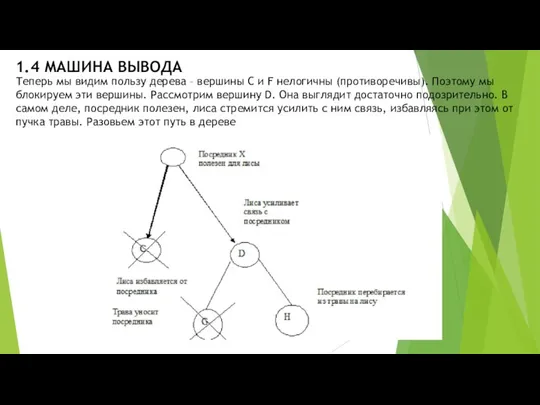
1.4 МАШИНА ВЫВОДА
Теперь мы видим пользу дерева – вершины C и F нелогичны (противоречивы). Поэтому мы блокируем эти вершины. Рассмотрим вершину D. Она выглядит достаточно подозрительно. В самом деле, посредник полезен, лиса стремится усилить с ним связь, избавляясь при этом от пучка травы. Разовьем этот путь в дереве

1.4 МАШИНА ВЫВОДА
В траве обитают живые существа, которые спасаясь от воды, перебираются на лису. Таких живых существ, кроме насекомых, нам не известно. Мы должны заблокировать вершину H.
Итак, мы видим, что путем построения дерева гипотез можно существенно раскрыть суть явления или задачи. Этот механизм следует взять на употребление и в интеллектуальных системах он действительно широко используется. Другое дело, опять возникает проблема, как оценивать вершины с точки зрения их перспективности или бесперспективности. Этой цели уже служит та или иная математическая теория. В частности, можно использовать механизм Саати, механизм решения логических систем уравнений с неопределенностями и др. В каждом узле дерева гипотез имеется набор гипотез и следствий из них, приведший в эту вершину. Так, в вершине H этот набор гипотез такой:
α − посредник полезен для лисы (0.8)
β − лиса усиливает связь с посредником (0.9)
γ − посредник перебирается с травы на лису (?)
ε − в траве нет полезных посредников (0.8)

1.4 МАШИНА ВЫВОДА
Здесь в скобках указаны меры доверия к формулам (составляются экспертами). Между этими формулами имеются логические зависимости. Запишем эти зависимости вместе с исходными данными:

1.4 МАШИНА ВЫВОДА
В Нашем примере для простоты мы не использовали меры неопределенности (это отдельная задача). Приняли, что если мера неопределенности больше 0.5, то формула считается истинной, а если меньше либо равна 0.5, то формула считается ложной. Нетрудно видеть, что полученная система противоречива.
Итак, дерево гипотез основано на порождении предположений. В каждом узле дерева «накапливаются» предположения, полученные по ходу движения в этот узел. Предположения могут быть более-менее правдоподобными. Мы блокируем узел и запрещаем движение из него, если множество гипотез несовместно. Для этой цели нужно строить связи между гипотезами (отношения следствия) и решать систему с неопределенностями.
Все полученные решения должны давать новые гипотезы.
Систему с неопределенностями легко решить в каком-либо современном математическом пакете, например, в Excel − с помощью пакета Поиск Решения.