Арифметические операции в системах счисления

1 – 10
2 - 5
3 - 4
4 - 1
5 - 2
6 - 8
7 - 3

Укажите, какие числа записаны
с ошибками и аргументируйте ответ:
1237, 30064, 12ААС0920, 134767
Какое минимальное основание должна иметь
система счисления, если в ней
могут быть записаны числа: 10, 21, 201, 1201
Какой цифрой заканчивается четное двоичное число?
Какой цифрой заканчивается нечетное двоичное число?

Арифметические операции в системах счисления

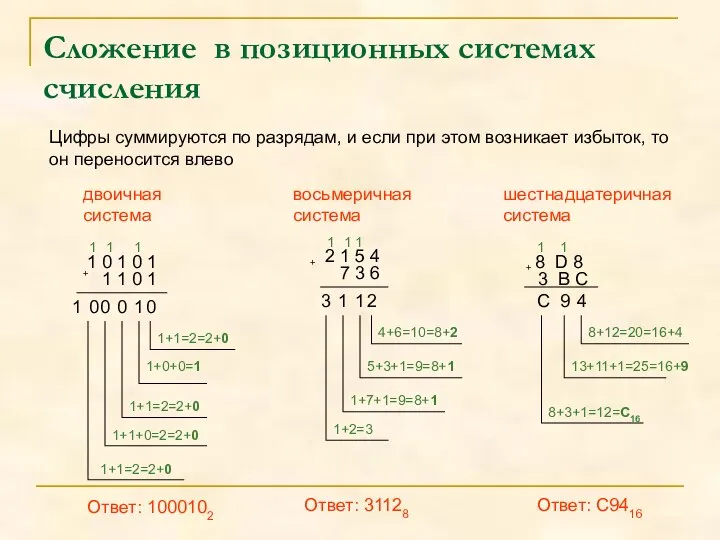
Сложение в позиционных системах счисления
Цифры суммируются по разрядам, и если при этом возникает избыток, то он переносится влево
1 0 1 0 1
+
1 1 0 1
двоичная
система
0
1+1=2=2+0
1
1
1+0+0=1
0
1+1=2=2+0
1
0
1+1+0=2=2+0
1
0
1+1=2=2+0
1
Ответ: 1000102
2 1 5 4
+
7 3 6
2
4+6=10=8+2
1
1
5+3+1=9=8+1
1
1+7+1=9=8+1
1
3
1+2=3
восьмеричная
система
1
Ответ: 31128
шестнадцатеричная
система
8 D 8
+
3 B C
4
8+12=20=16+4
1
9
13+11+1=25=16+9
8+3+1=12=C16
C
1
Ответ: C9416

Примеры:
1001100
1010110

Примеры
1 3 1 1
2 3 5 2

Пример:
С В А16
+ A 5 916
1 7 1 3

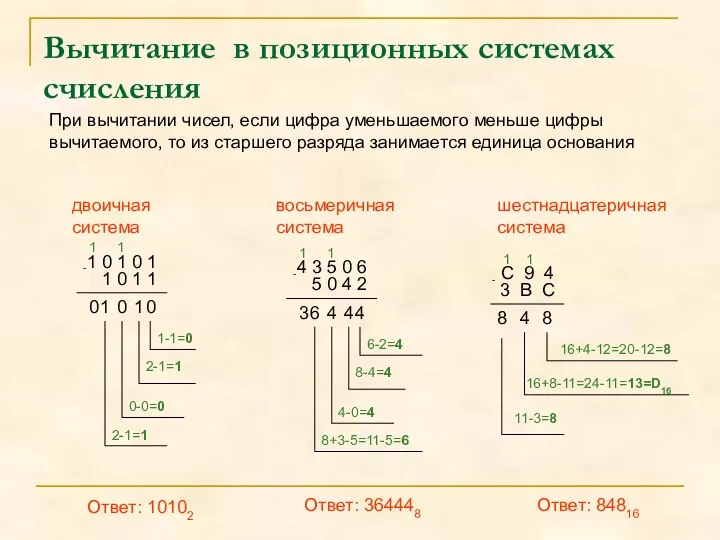
Вычитание в позиционных системах счисления
При вычитании чисел, если цифра уменьшаемого меньше цифры вычитаемого, то из старшего разряда занимается единица основания
двоичная
система
Ответ: 10102
восьмеричная
система
Ответ: 364448
шестнадцатеричная
система
Ответ: 84816
1 0 1 0 1
-
1 0 1 1
0
1-1=0
1
1
2-1=1
0
0-0=0
1
2-1=1
1
0
4 3 5 0 6
-
5 0 4 2
4
6-2=4
1
4
8-4=4
4
4-0=4
6
8+3-5=11-5=6
1
3
С 9 4
-
3 В С
8
16+4-12=20-12=8
1
4
16+8-11=24-11=13=D16
8
11-3=8
1

Примеры:
1110
11110

Примеры
5 0 4
2 7 4

Пример:
А 5 916
– 1 В А16
8 9 F

3∙3=9=8+1
Умножение в позиционных системах счисления
При умножении многозначных чисел в различных позиционных системах применяется алгоритм перемножения чисел в столбик, но при этом результаты умножения и сложения записываются с учетом основания системы счисления
двоичная
система
Ответ: 1010111112
восьмеричная
система
Ответ: 133518
1 1 0 1 1
х
1 1 0 1
1 1 0 1 1
1 1 0 1 1
1 1 0 1 1
1 0 1 0 1 1 1 1 1
1+1+1=3=2+1
1
1+1+1=3=2+1
1
1+1=2=2+0
1
1
1 6 3
х
6 3
5 3 1
1
6∙3+1=19=16+3=2∙8+3
2
1∙3+2=5
1 2 6 2
6∙3=18=16+2=8∙2+2
6∙6+2=38=32+6=4∙8+6
2
4
6∙1+4=10=8+2
1 3 3 5 1
6+5=11=8+3
1

Деление в позиционных системах счисления
Деление в любой позиционной системе производится по тем же правилам, как и деление углом в десятичной системе. При этом необходимо учитывать основание системы счисления.
двоичная
система
Ответ: 10,12
восьмеричная
система
Ответ: 638
1 0 0 0 1 1
1 1 1 0
1
1 1 1 0
1 1 1 0
1 1
1
,
0
0
1
0
1 3 3 5 1
1 6 3
6
1 2 6 2
5 3
1
3
5 3 1
0

Примеры:
×
111102:1102=
1011011
101

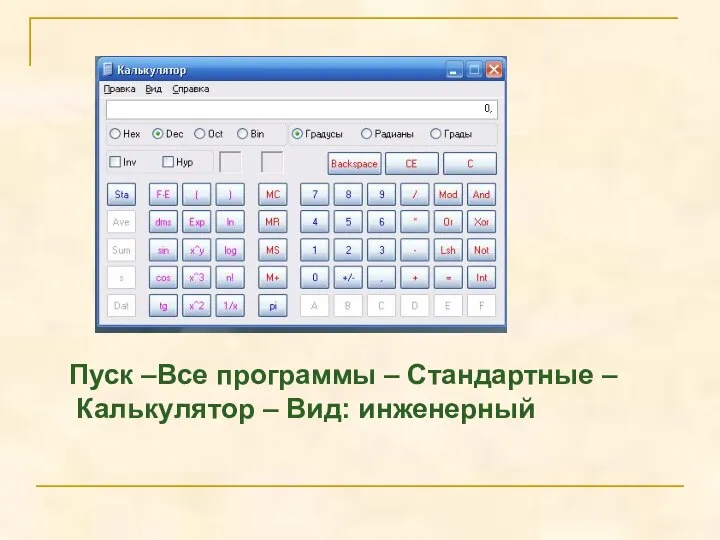
Пуск –Все программы – Стандартные –
Калькулятор – Вид: инженерный