Слайд 2Введение
“Кто владеет информацией - тот владеет миром.”
Nathan Mayer Rothschild

Слайд 3Цель работы
Разработать решение для групп людей, которые обеспокоены безопасностью общих данных, хранящихся

в графическом виде.
Слайд 4Задачи
Найти способ шифрования изображений.
Изучить механизм защиты ключа шифрования.
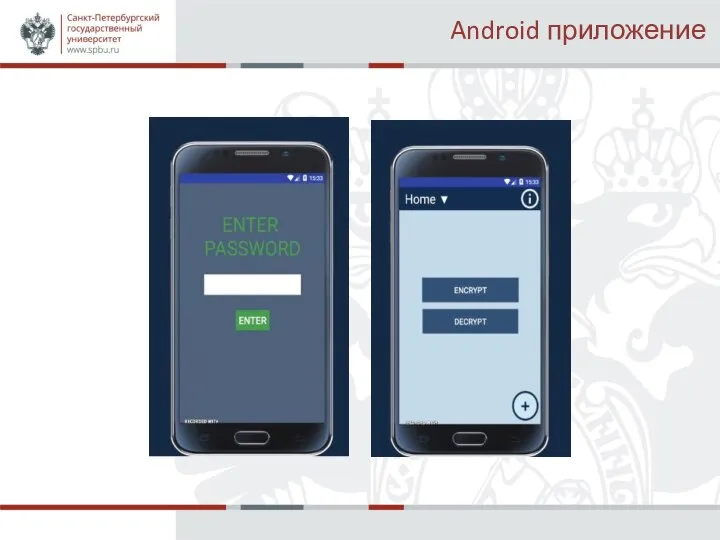
Реализовать демонстрационное приложение на

платформе Android.
Слайд 6Алгоритм шифрования
Задаем n — количество чисел в ключе, по которому будем шифровать.

([k1,k2,k3,...kn])
Генерируем эти числа, которые будут принимать значения в диапазоне от 0 до 255, и заносим в массив key, размером n.
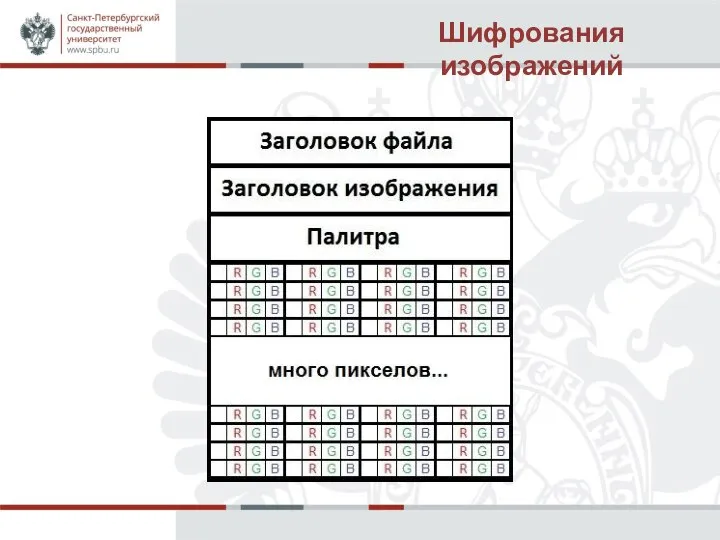
BMP-файл переводим в целочисленный массив srcPixels, каждый элемент которого содержит информацию о цвете соответствующего ему пикселя, т.е. этот массив будет длиной bitmap.height() * bitmap.width()
Слайд 7RGB компоненты i-го элемента массива srcPixels меняем следующим образом:
R = (R + key[i % (key.length - 3)]) % 256
G = (G + key[i % (key.length - 3) + 1]) % 256
B = (B + key[i % (key.length - 3) + 2]) % 256
Из, уже измененного,

массива srcPixels создаем новое изображение, которое и будет являться зашифрованным.
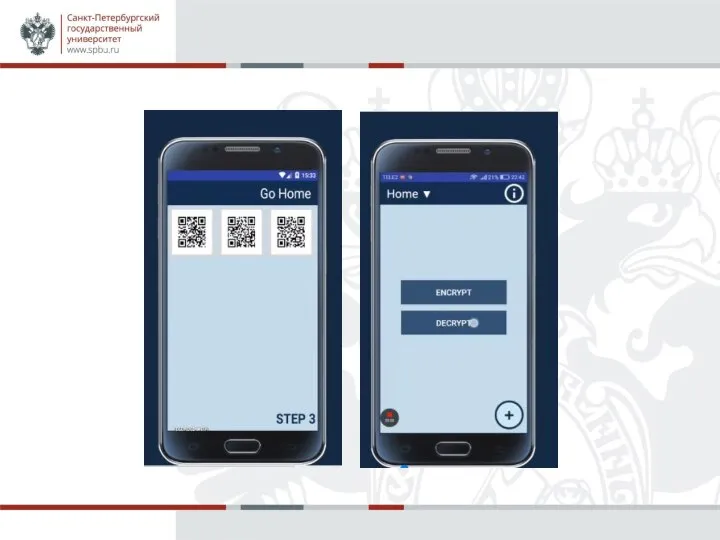
Генерируем QR-код, в котором записаны элементы массивa key.
Слайд 8Secret Sharing
Одиннадцать ученых работают над секретным проектом. Они хотят запереть документы в

шкафу, чтобы кабинет можно было открыть, если и только если присутствуют шесть или более ученых. Какое минимальное количество замков необходимо? Какое минимальное количество ключей для замков, должен носить каждый учёный?
Слайд 9Наша цель состоит в том, чтобы разделить данные D на n кусков

D1, .....Dn таким образом, что:
знание любого k или более Di частей, делает D легко вычислимым;
знание любого k-1 или меньшего количества частей Di оставляет D полностью неопределенным (в том смысле, что все его возможные значения одинаково вероятны).
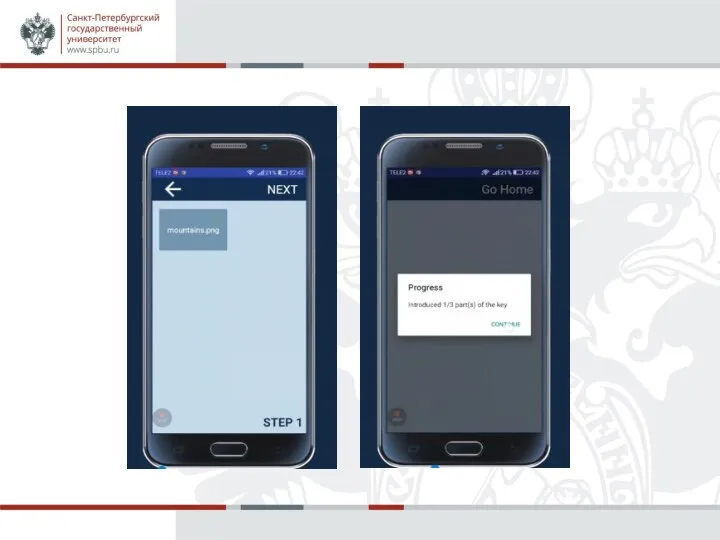
Слайд 11Подготовительная фаза
Пусть нужно разделить секрет M между n сторонами таким образом, чтобы любые k участников

могли бы восстановить секрет.
Слайд 12Генерация долей секрета
Теперь вычисляем «тени» — значения построенного выше многочлена, в n различных

точках, причём x ≠ 0
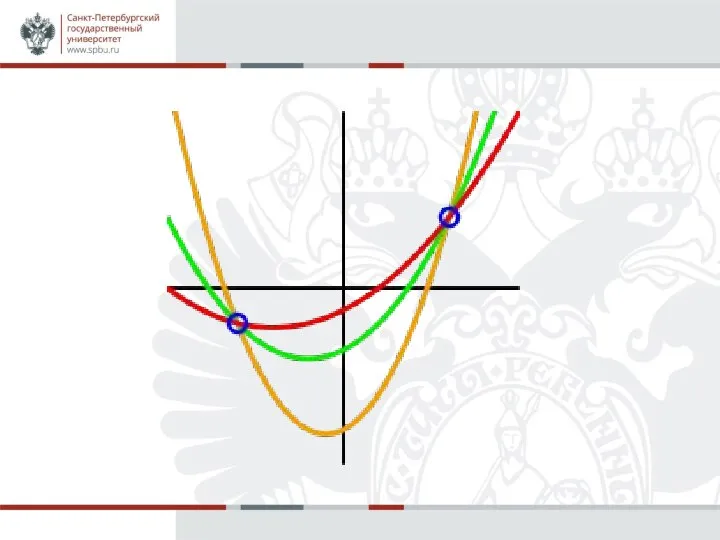
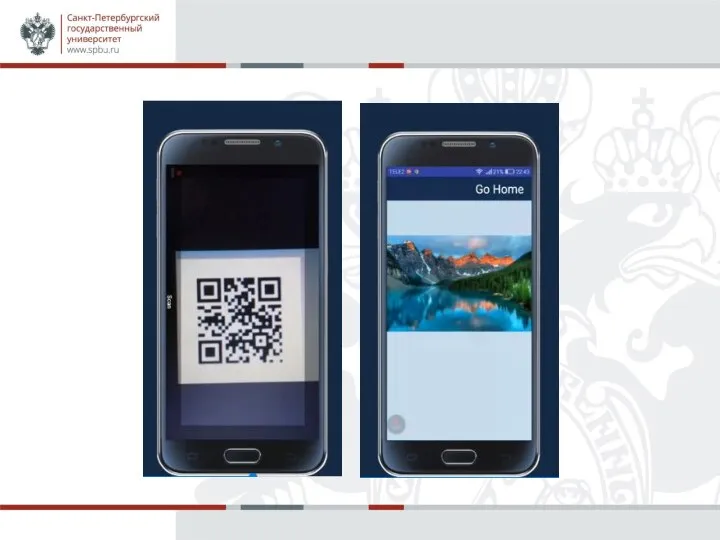
Слайд 13Восстановление секрета
Теперь любые k участников, зная координаты k различных точек многочлена, смогут восстановить многочлен и

все его коэффициенты, включая последний из них — разделяемый секрет.
Слайд 19Заключение
Все поставленные цели и задачи были выполнены:
Был разработан способ шифрования изображений
Была изучена

и применена схема разделения секрета Шамира
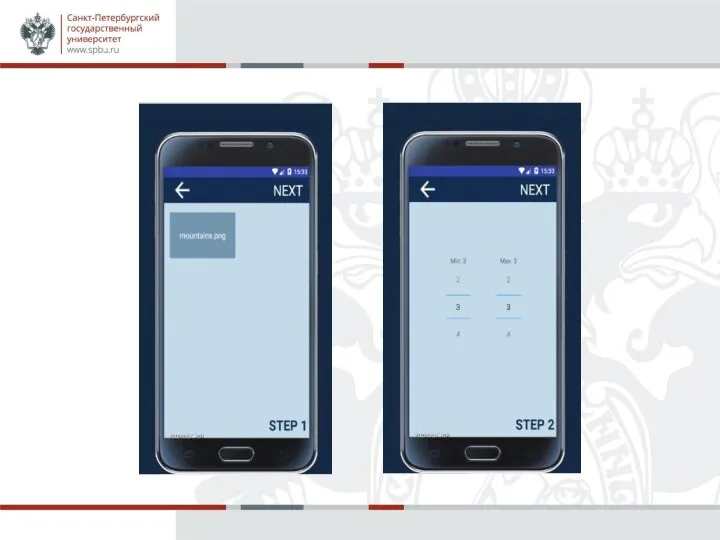
Было разработано приложение на платформу Android, выполняющее шифрование и дешифрование изображение с разделение секрета.
Слайд 20Дальнейшее направление исследования
На данный момент, целью является создания сервиса для хранения изображений,

в котором все элементы будут храниться в зашифрованном виде.
Расшифровать данные изображения можно будет только в том случае, если к сервису в данный момент времени подключено определенное количество пользователей, которым предоставлен доступ.
Причем, при подключении меньшего количества людей, изображения невозможно будет расшифровать.












 Защита информации. Антивирусная защита
Защита информации. Антивирусная защита Системное программное обеспечение
Системное программное обеспечение Программное обеспечение для партнеров
Программное обеспечение для партнеров skanery_2
skanery_2 Исполнитель Водолей
Исполнитель Водолей Lorem ipsum dolor sit amet, consectetuer adipiscing elit
Lorem ipsum dolor sit amet, consectetuer adipiscing elit Средства анализа и визуализации данных
Средства анализа и визуализации данных Концепция электронного голосования
Концепция электронного голосования Презентация на тему Перевод чисел из одной системы счисления в другую
Презентация на тему Перевод чисел из одной системы счисления в другую  Документ, его характеристики (формуляр, структура, юридическая сила, вид) и функции. Связь информации и документа
Документ, его характеристики (формуляр, структура, юридическая сила, вид) и функции. Связь информации и документа Операционная система Windows
Операционная система Windows Информационные технологии
Информационные технологии Анатомия распределенной команды. Коммуникация, гибкость, процессы
Анатомия распределенной команды. Коммуникация, гибкость, процессы Защита web-сайта Моё электронное портфолио
Защита web-сайта Моё электронное портфолио Технология решения задания С1
Технология решения задания С1 Теория игр. Аналитическая работа по статье Croson “Gender and Culture”
Теория игр. Аналитическая работа по статье Croson “Gender and Culture” Задание №2. Разработка презентации в приложении PowerPoint на базе первого задания
Задание №2. Разработка презентации в приложении PowerPoint на базе первого задания Программно-аппаратный комплекс для диагностики катаракты глаза с помощью мобильного телефона
Программно-аппаратный комплекс для диагностики катаракты глаза с помощью мобильного телефона Операционная система
Операционная система Active Directory (каталог) - бұл қандайда бір обьект туралы мәліметтерді сақтауға қолданылатын ақпараттық
Active Directory (каталог) - бұл қандайда бір обьект туралы мәліметтерді сақтауға қолданылатын ақпараттық Parallel от TaxiTime. Аналитика для увеличения прибыли автопарков
Parallel от TaxiTime. Аналитика для увеличения прибыли автопарков Рекламный кейс книжной поисковой системы
Рекламный кейс книжной поисковой системы Фрактальная графика на паскале
Фрактальная графика на паскале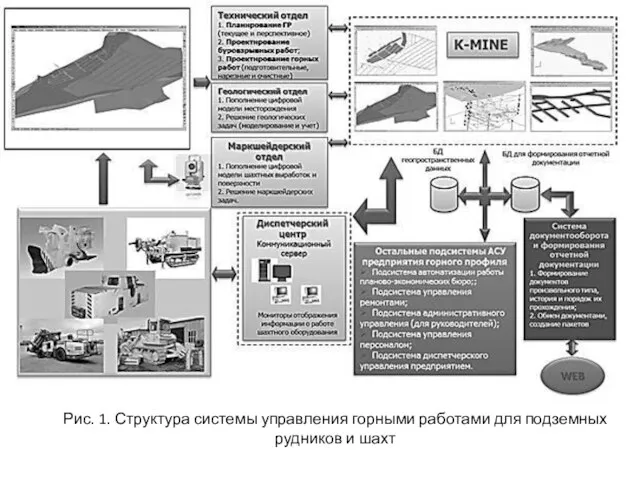 IT в управлении горными работами
IT в управлении горными работами Презентация на тему Линейные алгоритмы (4 класс)
Презентация на тему Линейные алгоритмы (4 класс)  Автоматизированное тестирование
Автоматизированное тестирование Голоса выставочной индустрии. Шаблон
Голоса выставочной индустрии. Шаблон Продвижение учреждения дополнительного образования в социальных сетях
Продвижение учреждения дополнительного образования в социальных сетях