Логические основы работы компьютера

ВВЕДЕНИЕ:
Мы познакомились с устройством компьютера и узнали, что
в процессе обработки двоичной информации процессор выполняет арифметические и логические операции. Поэтому для получения представлений об устройстве компьютера необходимо познакомиться и с основными логическими элементами, лежащими в основе построения компьютера и работающими аналогично переключательным схемам. (ф-1) Для понимания принципа работы таких элементов начнем это знакомство с основных начальных понятий формальной логики.
Термин «логика» происходит от древнегреческого logos, означающего «слово, мысль, понятие, рассуждение, закон».
2

Логика - наука, изучающая законы и формы мышления.
Этапы развития логики:
I этап - формальная логика. Основатель — Аристотель (384-322 гг. до н.э.), ввел основные формы абстрактного мышления.
II этап - математическая логика. Основатель - немецкий ученый и философ Лейбниц (1642-1716), предпринял попытку логических вычислений.
III этап - математическая логика (булева алгебра). Основатель - английский математик Джордж Буль (1815-1864), ввел алфавит, орфографию и грамматику для математической логики.
3

Алгебра логики - это математический аппарат с помощью которого записывают (кодируют), упрощают, вычисляют и преобразовывают логические высказывания.
Высказывание (суждение) - повествовательное предложение,
о котором можно сказать, истинно оно или ложно.
Высказывание может принимать только одно из двух логических значений - истинно (1) или ложь (0).
Примеры высказывании:
Земля - планета Солнечной системы (истинное высказывание).
3 + 6 > 10 (ложное высказывание).
4

Утверждение — суждение, которое требуется доказать или опровергнуть, например, сумма внутренних углов треугольника равна180°.
Рассуждение — цепочка высказываний или утверждений, определённым образом связанных друг с другом, например, если хотите начать работать на компьютере, то необходимо сначала включить электропитание.
Умозаключение — логическая операция, в результате которой из одного или нескольких данных суждений получается (выводится) новое суждение.
Область знаний, которая изучает истинность или ложность высказываний (суждений), называется математической логикой.
Утверждения в математической логике называются логическими выражениями.
5

Объясните, почему следующие предложения не являются высказываниями:
Уходя, гасите свет.
Какого цвета этот дом?
Посмотрите в окно.
6

Высказывания бывают
простые и сложные.
Простое высказывание (логическая переменная)
содержит только одну простую мысль. Логические переменные обычно обозначаются буквами латинского алфавита : A, В, С, D...
Например, А = {Квадрат - это ромб}.
Сложное высказывание (логическая функция)
содержит несколько простых мыслей, соединенных между собой с помощью логических операций.
Например,
F(A,B) = {Лил дождь, (и) дул холодный ветер}.
А В
7

Значение логической функции можно определить с помощью специальной таблицы (таблицы истинности). Таблица истинности - таблица, в которой перечислены все возможные значения входящих логических переменных и соответствующие им значения функции.
Например:
А и В — логические переменные, n = 2
F — логическая функция
Количество строк (q) в таблице истинности определяется по формуле:
q = 2n
n - кол-во переменных
8

Логический элемент (вентиль) –
часть электронной логической схемы, которая выполняет элементарную логическую операцию.
Каждый логический элемент имеет свое условное обозначение, имеет один или несколько входов, на которые подаются сигналы «высокого» напряжения («1») и «низкого» напряжения («0»), и только один выход.
9

Любое сложное высказывание можно записать с помощью основных логических операций
И, ИЛИ, НЕ.
С помощью логических схем
И, ИЛИ, НЕ
можно реализовать любую логическую функцию,
описывающую работу различных устройств компьютера.
13

Другие логические операции
4. Импликация (логическое следование), от лат. implicatio — тесно связываю:
• соответствует речевому обороту ЕСЛИ...ТО
(в естественном языке: если А, то В
В, если А
В необходимо для А
А достаточно для В
А только тогда, когда В
В тогда, когда А
Все А есть В;
• обозначение: , =>;
14

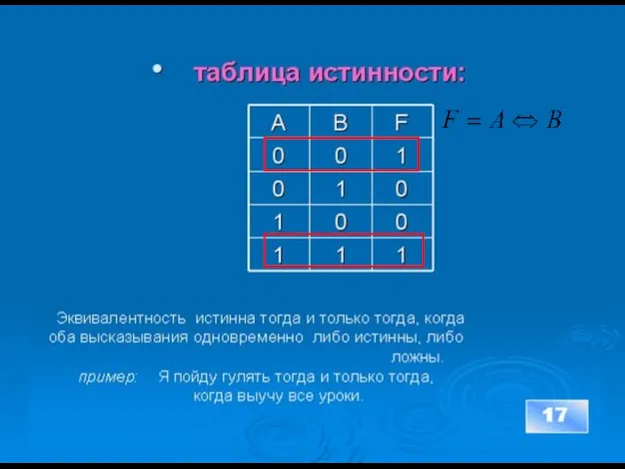
5. ЭКВИВАЛЕНТНОСТЬ (равнозначность), от лат. Aequivalens – равноценное.
coответствует речевым оборотам ЭКВИВАЛЕНТНО:
необходимо и достаточно для тогда и только тогда, когда;
обозначение: =, , <=>;
16

Порядок выполнения логических операций:
1) операция в скобках;
2) отрицание;
3) логическое умножение;
4) логическое сложение;
5) импликация;
6) эквивалентность.
18

Задание 3: Запишите на языке алгебры логики следующие высказывания:
Я поеду в Киев и если встречу друзей, то мы интересно проведем время.
Если я поеду в Киев и встречу там друзей, то мы интересно проведем время.
Неверно, что если погода пасмурная, то идет дождь тогда и только тогда, когда нет ветра.
21
F1 = A*(B⭢C)
F2 = A*B⭢C
F3 = ¬ (A⭢ B = C)

ТЕСТИРОВАНИЕ (ф-2)
22

ПОСТРОЕНИЕ ТАБЛИЦ ИСТИННОСТИ ДЛЯ СЛОЖНЫХ ЛОГИЧЕСКИХ ВЫРАЖЕНИЙ.
23

При изучении работы различных устройств компьютера приходится рассматривать такие его логические элементы, в которых реализуются сложные логические выражения. Поэтому необходимо научиться определять результат этих выражений, то есть строить для них таблицы истинности.
24

Порядок построения таблиц истинности
по булеву выражению:
1) определить число переменных;
2) определить число строк в таблице истинности:
q = 2n (+ 1 на заголовок)
3) записать все возможные значения переменных;
4) определить количество логических операций и их порядок;
3 операции + 3 переменных = 6 столбцов
5) записать логические операции в таблицу
истинности и определить для каждой значение;
6) подчеркнуть значения переменных, для которых F = 1.
26

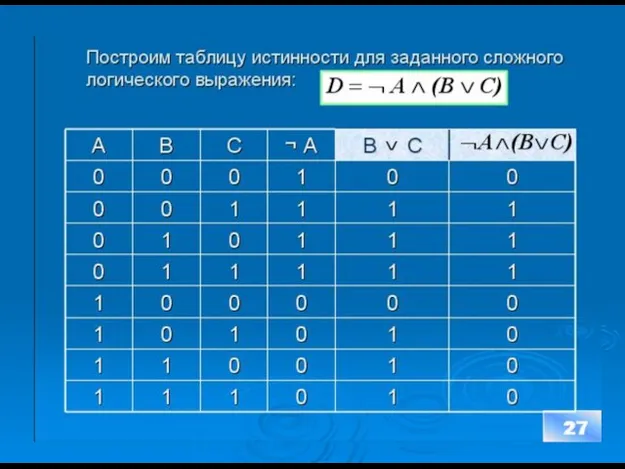
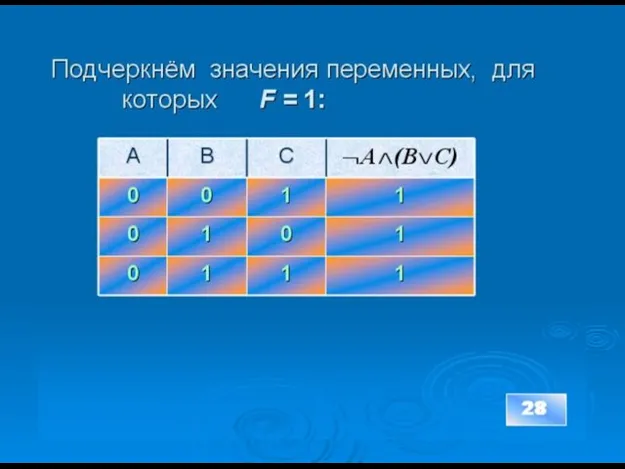
Построим таблицу истинности для заданного сложного логического выражения:
27