Слайд 2Содержание лекции:
Алгоритмы и способы представления
2. Реализация стандартных алгоритмических
конструкций на MatLab
3.

Алгоритмически неразрешимые задачи
4. Примеры задач и реализующие их
алгоритмы
5. Функции многих переменных
Слайд 3Алгоритм
Абу Джафар Муха́ммад ибн Муса́ аль-Хорезми́
ок. 783 — ок. 850)

Слайд 4Алгоритм – одна из основных категорий
математики
Основные требования:
- дискретность
- детерминированность
- конечность
- результативность
- массовость
Итог

– единственный конечный результат за конечное число шагов, примененное к допустимым исходным данным
Слайд 5Алгоритм - определение
Алгоритм – конечная последовательность однозначных предписаний, исполнение которых позволяет с

помощью конечного числа шагов получить решение поставленной задачи, однозначно определяемое исходными данными
Слайд 6Алгоритм Евклида
Поиск наибольшего общего делителя двух чисел

Слайд 7Алгоритмически неразрешимые задачи
- Проблема единичной матрицы
- Проблема умирающей матрицы
-Игра «Жизнь»
-10 проблема Гильберта
-

поиск начала серии из n девяток в числе π
Вычисление нечетного совершенного числа
Слайд 8Способы представления алгоритмов
СЛОВЕСНЫЙ

Слайд 9Способы представления алгоритмов
ФОРМУЛЬНО-
СЛОВЕСНЫЙ

Слайд 10Способы представления алгоритмов
ТАБЛИЧНЫЙ

Слайд 11Способы представления алгоритмов
Графический

Слайд 12Способы представления алгоритмов
Графический

Слайд 13Типы алгоритмов
- Линейный
Ветвящийся
Циклический
Сложной структуры

Слайд 17Полярные и декартовые координаты

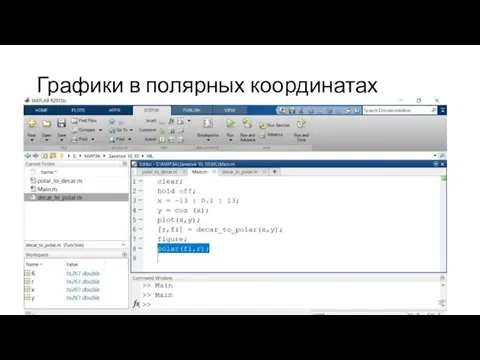
Слайд 18Полярные и декартовые координаты
function [ x,y ] = polar_to_decar( r,fi )
x =
![Полярные и декартовые координаты function [ x,y ] = polar_to_decar( r,fi )](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/909254/slide-17.jpg)
r*cos(fi);
y = r*sin(fi);
end
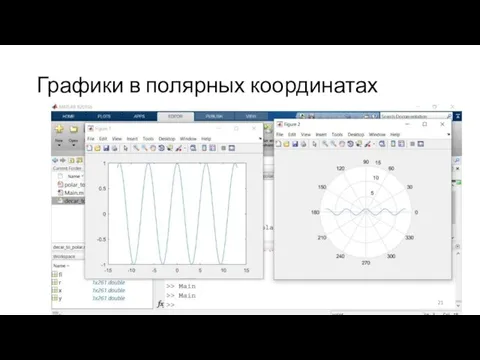
Слайд 19Полярные и декартовые координаты
function [ r,fi ] = decar_to_polar( x,y )
r =
![Полярные и декартовые координаты function [ r,fi ] = decar_to_polar( x,y )](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/909254/slide-18.jpg)
sqrt(x^2 + y^2);
fi = atan2(y,x);
end
Слайд 23Функции многих переменных
Задача
Построить двумерные и трехмерные графики параметрически заданной линии:
x(t)=t*sin(t), y(t)= t*cos(t)

при t от 0 до 10 π
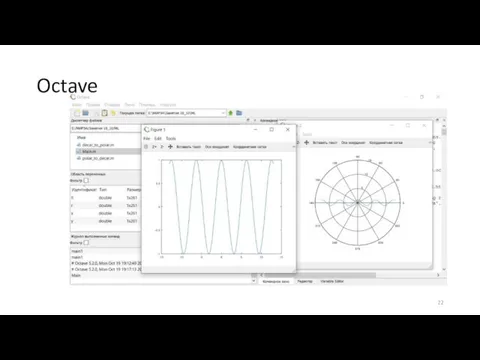
Слайд 24Функции многих переменных
Создаем функцию f11 в файле с именем f11.m
function[x,y] = f11(t)
x
![Функции многих переменных Создаем функцию f11 в файле с именем f11.m function[x,y]](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/909254/slide-23.jpg)
= t.*sin(t);
y = t.*cos(t);
end
Слайд 25Функции многих переменных
Создаем сценарий в файле main.m
clear;
t = 0:0.1:10*pi;
[x,y]=f11(t);
comet3(x,y,t);
title('figure');
Вызываем сценарий в

командном окне
>>main
Слайд 27Функции многих переменных
Задача
Построить график (поверхность) функции двух переменных

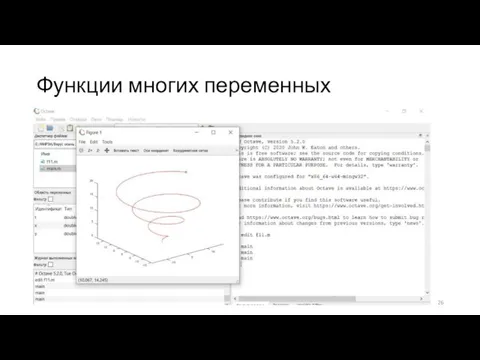
Слайд 28Функции многих переменных
hold off;
x=-1:0.1:1;
y=-2:0.1:2;
[X,Y]=meshgrid(x,y);
Z = exp(-X.^2 - Y.^2);
surf(X,Y,Z)
![Функции многих переменных hold off; x=-1:0.1:1; y=-2:0.1:2; [X,Y]=meshgrid(x,y); Z = exp(-X.^2 - Y.^2); surf(X,Y,Z)](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/909254/slide-27.jpg)
















![Полярные и декартовые координаты function [ x,y ] = polar_to_decar( r,fi )](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/909254/slide-17.jpg)
![Полярные и декартовые координаты function [ r,fi ] = decar_to_polar( x,y )](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/909254/slide-18.jpg)

![Функции многих переменных Создаем функцию f11 в файле с именем f11.m function[x,y]](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/909254/slide-23.jpg)


![Функции многих переменных hold off; x=-1:0.1:1; y=-2:0.1:2; [X,Y]=meshgrid(x,y); Z = exp(-X.^2 - Y.^2); surf(X,Y,Z)](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/909254/slide-27.jpg)
 Относительные и абсолютные ссылки в Microsoft Excel
Относительные и абсолютные ссылки в Microsoft Excel Переменные. Присваиваем значения
Переменные. Присваиваем значения 26 урок 8 клас Структура веб-сторінок Поняття про мову HTML 1
26 урок 8 клас Структура веб-сторінок Поняття про мову HTML 1 Биография И.А. Крылова
Биография И.А. Крылова Решение систем линейных уравнений при помощи компьютерных технологий
Решение систем линейных уравнений при помощи компьютерных технологий Интеграция с 1С: Документооборот. Программный интерфейс
Интеграция с 1С: Документооборот. Программный интерфейс Строки в C#
Строки в C# Сторителлинг
Сторителлинг Информационная система Покупка билетов в кино
Информационная система Покупка билетов в кино Пресс-релиз – основной инструмент PR
Пресс-релиз – основной инструмент PR Информационная система Авиакомпания
Информационная система Авиакомпания Круглый стол. Цифровая 3D-медицина. Тенденции развития научно-исследовательской работы студентов Арзамасского филиала ННГУ
Круглый стол. Цифровая 3D-медицина. Тенденции развития научно-исследовательской работы студентов Арзамасского филиала ННГУ SimShop. Mobile version comment
SimShop. Mobile version comment Smart. Оформление POS-кредитов просто, быстро и без бумаг
Smart. Оформление POS-кредитов просто, быстро и без бумаг Числовые типы данных. Стандартные функции языка Паскаль
Числовые типы данных. Стандартные функции языка Паскаль Разветвляющиеся вычислительные процессы
Разветвляющиеся вычислительные процессы Дочитываемость и досматриваемость
Дочитываемость и досматриваемость Системное мышление
Системное мышление Мини-хакатон ИИТТ
Мини-хакатон ИИТТ Трихадеры в rainbow six
Трихадеры в rainbow six Школьная библиотека в электронном образовательном пространстве
Школьная библиотека в электронном образовательном пространстве Байланыс негіздері
Байланыс негіздері Программирование (Python). Введение
Программирование (Python). Введение Школьный музей. Макет
Школьный музей. Макет Ошибки в тестировании ПО
Ошибки в тестировании ПО Самообразование в сфере QA
Самообразование в сфере QA Адаптация известных форм квестов для еврейского образования
Адаптация известных форм квестов для еврейского образования Образные коды двузначных чисел (урок 11)
Образные коды двузначных чисел (урок 11)