Содержание
- 2. Бинарный линейный классификатор XN={(x1,y1),…, (xN,yN)}, xi∈ RP, yi ∈{-1,+1} Цель: каждый новый входной вектор x отнести
- 3. Примеры задач Data mining классификация – отнесение объекта к одной из категорий (классов) на основании его
- 4. Линейная модель классификации
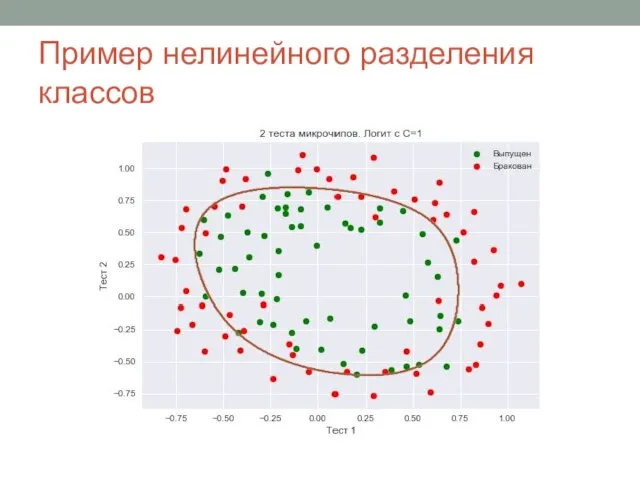
- 5. Пример нелинейного разделения классов
- 6. Confusion matrix (матрица ошибок классификации)
- 7. Метрики качества классификации Доля правильных ответов: Малоинформативна в задачах с неравными классами. Пример. Допустим, мы хотим
- 8. Метрики качества классификации precision (точность) и recall (полнота). Precision показывает долю объектов, названных классификатором положительными и
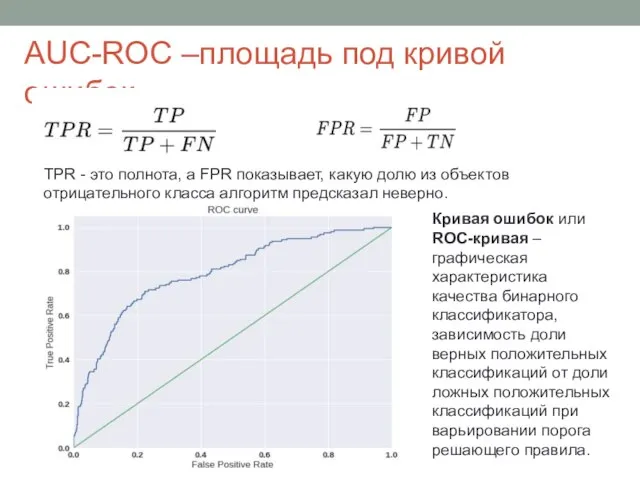
- 9. AUC-ROC –площадь под кривой ошибок TPR - это полнота, а FPR показывает, какую долю из объектов
- 10. AUC-ROC –площадь под кривой ошибок В идеальном случае, когда классификатор не делает ошибок (FPR = 0,
- 11. Чувствительность и специфичность Наряду с FPR и TPR при оценке качества классификации используют также понятия чувствительности
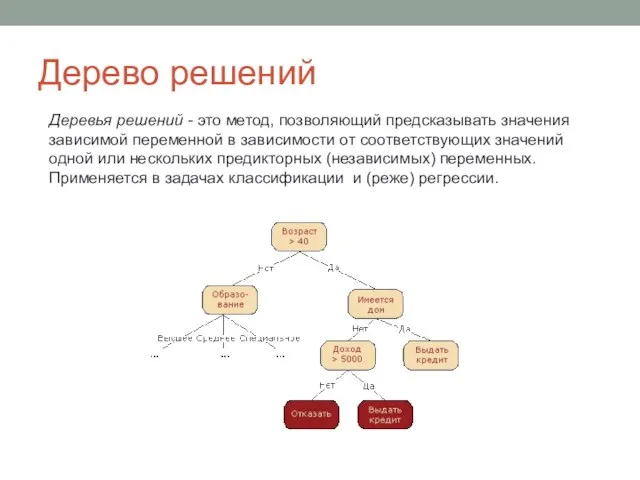
- 12. Дерево решений Деревья решений - это метод, позволяющий предсказывать значения зависимой переменной в зависимости от соответствующих
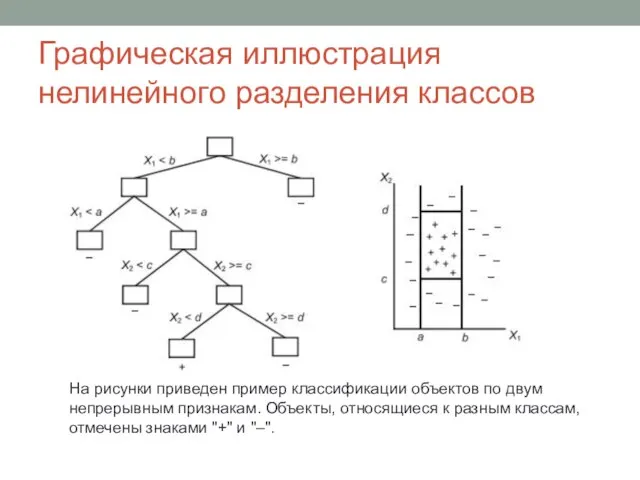
- 13. Графическая иллюстрация нелинейного разделения классов На рисунки приведен пример классификации объектов по двум непрерывным признакам. Объекты,
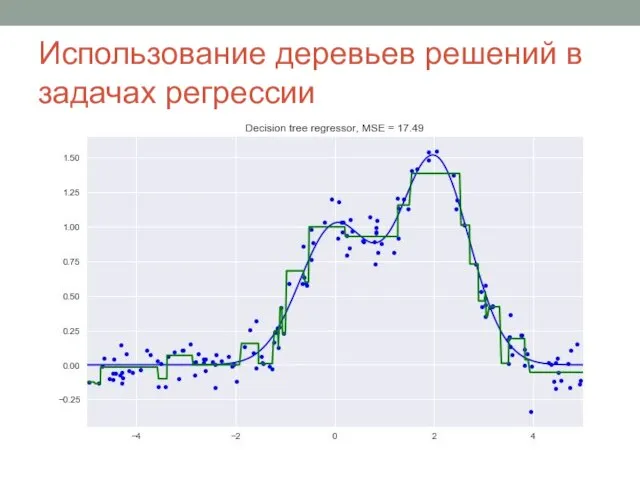
- 14. Использование деревьев решений в задачах регрессии
- 15. Этапы построения дерева решений 1. Выбор критерия точности прогноза 2. Выбор типа ветвления 3. Определение момента
- 16. Выбор типа ветвления (criterion) Есть различные способы выбирать очередной признак для текущего ветвления: Алгоритм ID3, где
- 17. Энтропия Энтропия Шеннона для системы с s возможными состояниями:
- 18. Прирост информации (ID3)
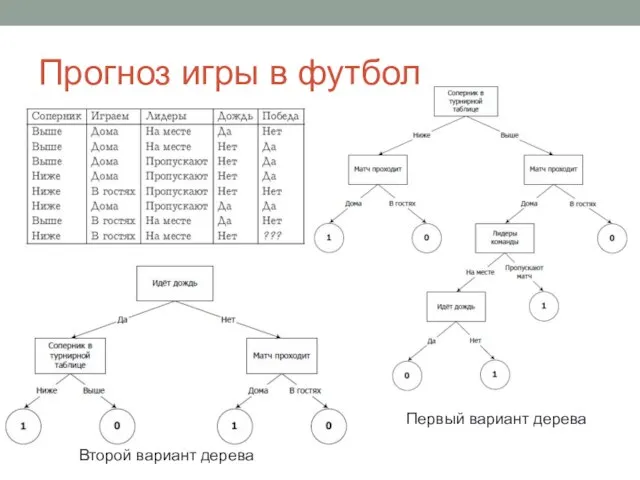
- 19. Прогноз игры в футбол Первый вариант дерева Второй вариант дерева
- 20. Вычисление энтропии и прироста информации
- 21. Нормализованный прирост информации (C4.5)
- 22. Индекс Gini (CART)
- 23. Правила разбиения (CART)
- 24. Правила остановки Минимальное число объектов, при котором выполняется расщепление (min_samples_split). В этом варианте ветвление прекращается, когда
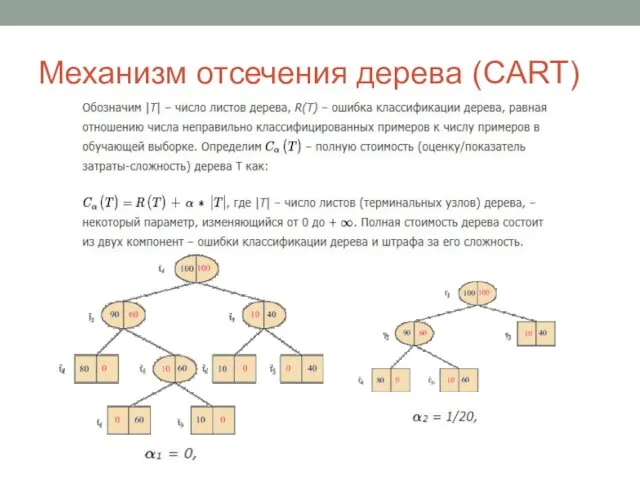
- 25. Механизм отсечения дерева (CART)
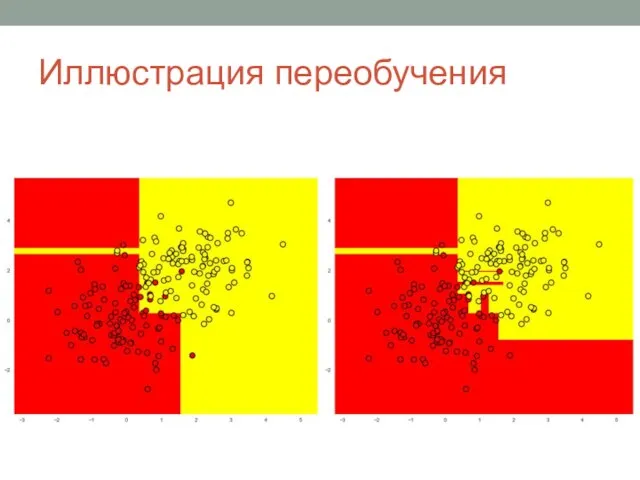
- 26. Иллюстрация переобучения
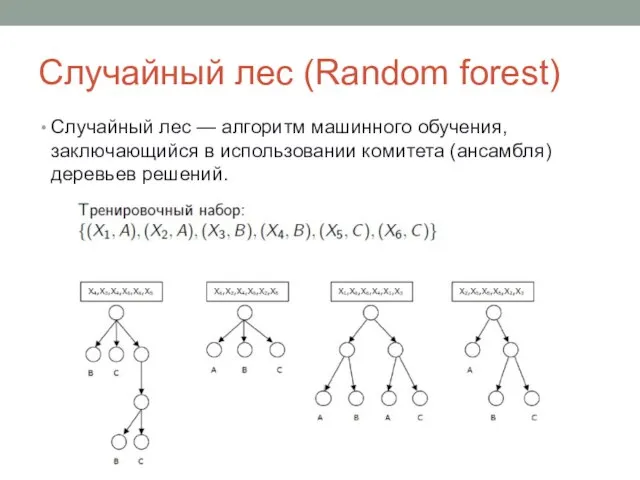
- 27. Случайный лес (Random forest) Случайный лес — алгоритм машинного обучения, заключающийся в использовании комитета (ансамбля) деревьев
- 28. Обучение случайного леса
- 30. Скачать презентацию


















 Технология программирования на языке python и разработка программ для машинного обучения
Технология программирования на языке python и разработка программ для машинного обучения Программирование на языке Python
Программирование на языке Python ИК Базы данных. Урок 6. Презентация
ИК Базы данных. Урок 6. Презентация Lektsia_GOST_R_ISO_MEK_12207_Osnovnye_protsessy_i_vzaimosvyaz_mezhdu_dokumentami_v_informatsionnoy_sisteme_soglasno_standartam
Lektsia_GOST_R_ISO_MEK_12207_Osnovnye_protsessy_i_vzaimosvyaz_mezhdu_dokumentami_v_informatsionnoy_sisteme_soglasno_standartam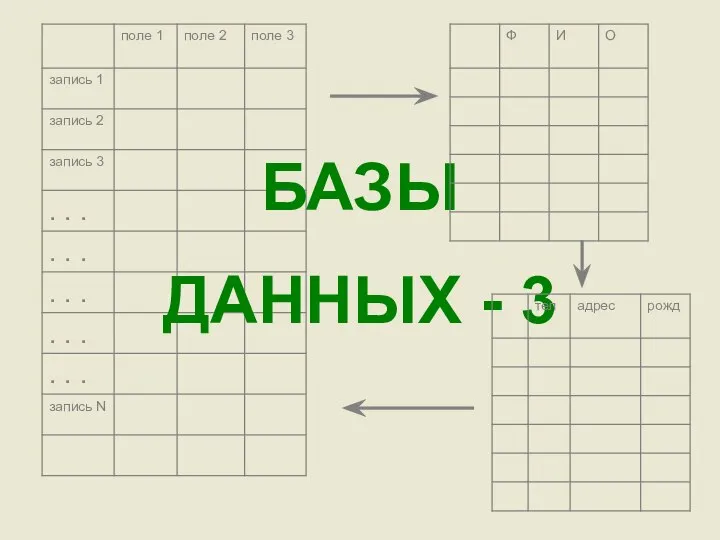 Базы данных-3
Базы данных-3 Информационные технологии в обработке текстов. Автоматическое чтение текста
Информационные технологии в обработке текстов. Автоматическое чтение текста Шрифт
Шрифт Мультимедийные презентации
Мультимедийные презентации Основы самоорганизующихся сетей
Основы самоорганизующихся сетей Аналитическия статья
Аналитическия статья 5 steps slides
5 steps slides Виртуальная реальность. Что это такое?
Виртуальная реальность. Что это такое? Network computer technician
Network computer technician Концепция Virtual logistics
Концепция Virtual logistics Типовые разветвляющиеся алгоритмы. Примеры
Типовые разветвляющиеся алгоритмы. Примеры Персональные данные: проблемы использования и защиты
Персональные данные: проблемы использования и защиты Алгоритмы со строковыми величинами. Решение задач
Алгоритмы со строковыми величинами. Решение задач Логирование ошибок КНД
Логирование ошибок КНД 4IZ110 - Informační a komunikační technologie
4IZ110 - Informační a komunikační technologie Анимация персонажа
Анимация персонажа Управление реальной памятью
Управление реальной памятью Понятие информационной системы (ИС)
Понятие информационной системы (ИС) Центр обработки данных
Центр обработки данных ОП БД Лекция_1
ОП БД Лекция_1 Отчет в рамках исполнения работ по государственному контракту на оказание услуг, выполнение работ
Отчет в рамках исполнения работ по государственному контракту на оказание услуг, выполнение работ Основы алгоритмизации (9 класс)
Основы алгоритмизации (9 класс) Презентация на тему Компьютерные вирусы
Презентация на тему Компьютерные вирусы  Создание рисунков из кривых
Создание рисунков из кривых