Содержание
- 2. * Деревья Ссылочная реализация бинарного дерева в связанной памяти Базовый тип узлов Elem. BT (Elem) представляетя
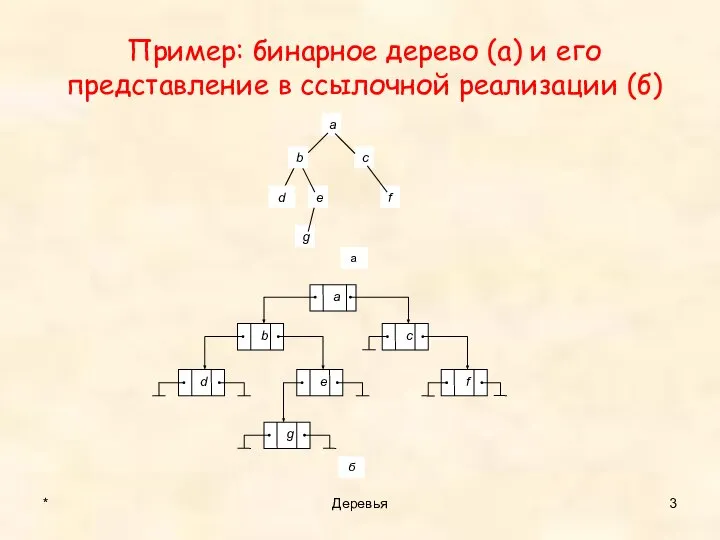
- 3. Пример: бинарное дерево (а) и его представление в ссылочной реализации (б) * Деревья
- 4. Набор основных функций для работы с бинарным деревом на основе ссылочной реализации Функция CreateBT формально специфицируется
- 5. В процедурно-модульной парадигме интерфейс АТД "Бинарное дерево” представлен в файле Btree.h, реализация основных функций для работы
- 6. Ссылочная реализация ограниченного бинарного дерева на базе вектора * Деревья
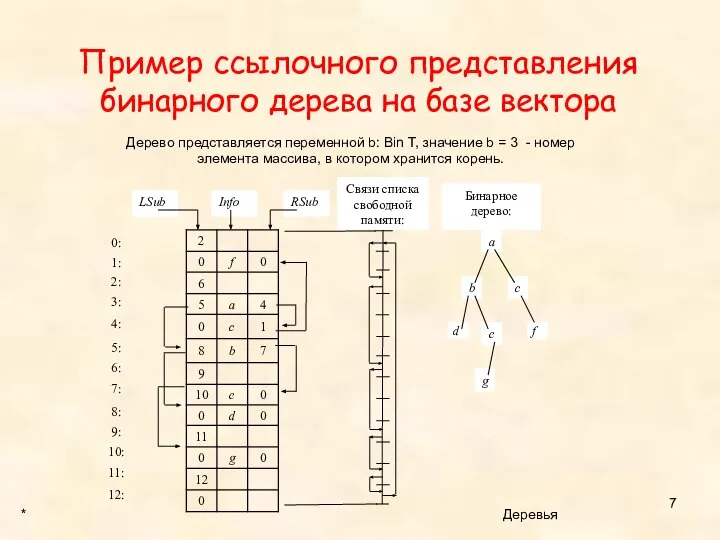
- 7. Пример ссылочного представления бинарного дерева на базе вектора * Деревья LSub Info RSub Связи списка свободной
- 8. * Деревья Примеры функций на бинарных деревьях Число узлов БД: 0, при T = Λ Nv(T)
- 9. * Деревья Примеры функций на бинарных деревьях Nat0 NLeaf (BinT t): { if (Null(t)) return 0;
- 10. * Деревья Высота БД: 0, при T = Λ H(T) = max (H(TL), H(TR)) +1, при
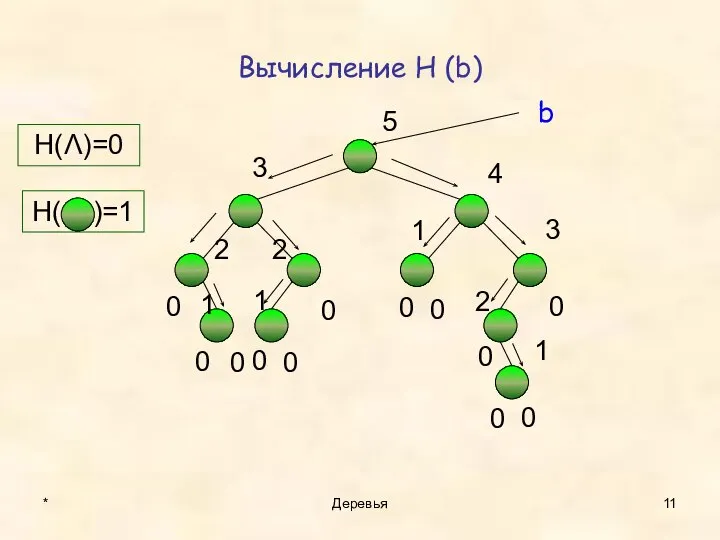
- 11. Вычисление H (b) * Деревья H(Λ)=0 0 0 1 0 2 0 0 1 0 2
- 12. * Деревья Проверить свойство дерева: для каждого узла БД имеем H(TL) – H(TR) = 1 Bool
- 13. Бинарные деревья с размеченными листьями (комбинации) Бинарное дерево с размеченными листьями - это либо знак («атом»,
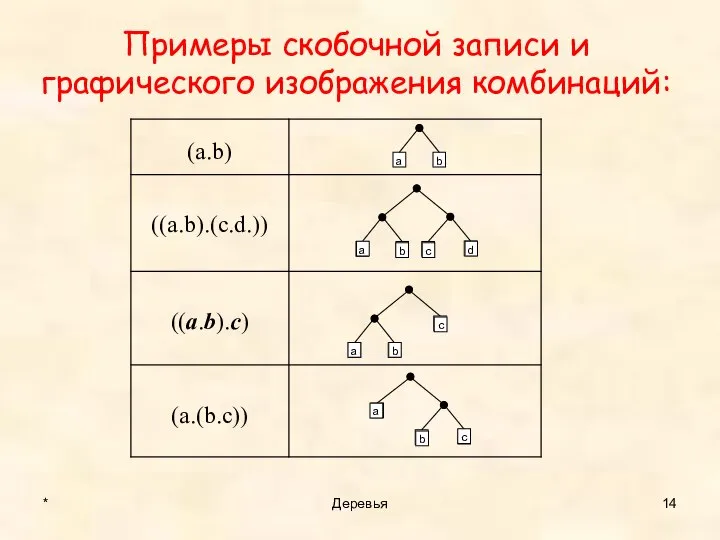
- 14. Примеры скобочной записи и графического изображения комбинаций: * Деревья a b c d a b c
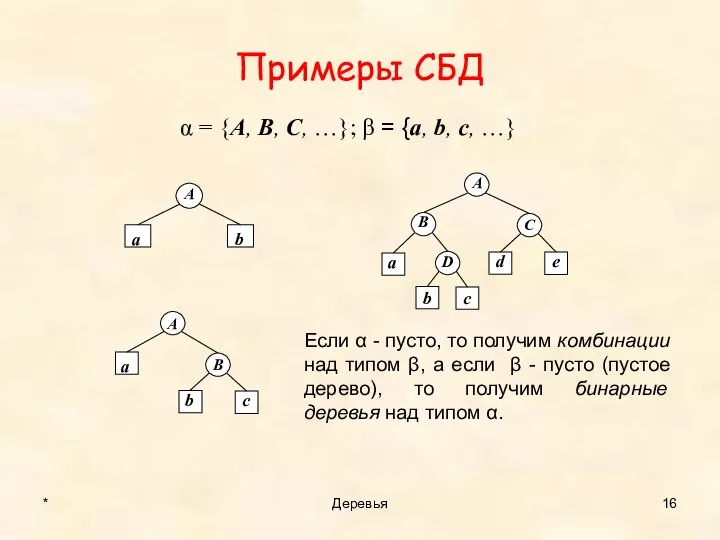
- 15. Cмешанное бинарное дерево (СБД) Можно ввести «гибрид» бинарных деревьев и комбинаций. Определим смешанное (расширенное, декорированное) бинарное
- 16. Примеры СБД * Деревья α = {A, B, C, …}; β = {a, b, c, …}
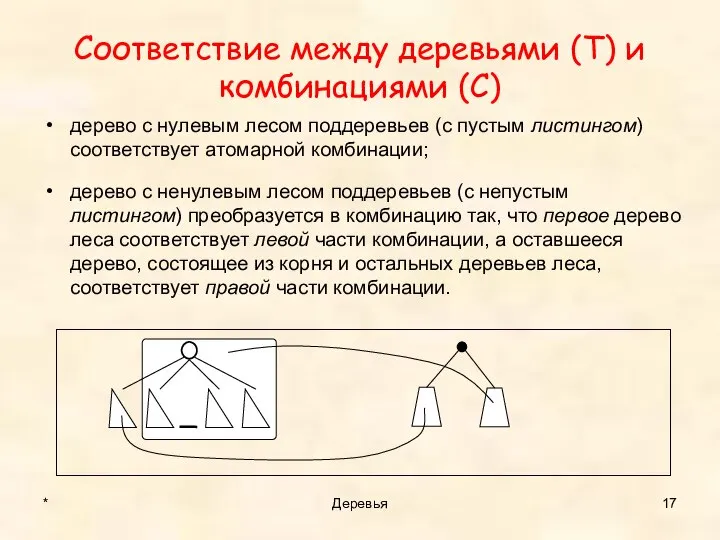
- 17. Соответствие между деревьями (T) и комбинациями (С) дерево с нулевым лесом поддеревьев (с пустым листингом) соответствует
- 18. Формально соответствие «дерево ⇒ комбинация» может быть описано функцией C(T) ≡ if Null(Listing(T)) then Root(T) else
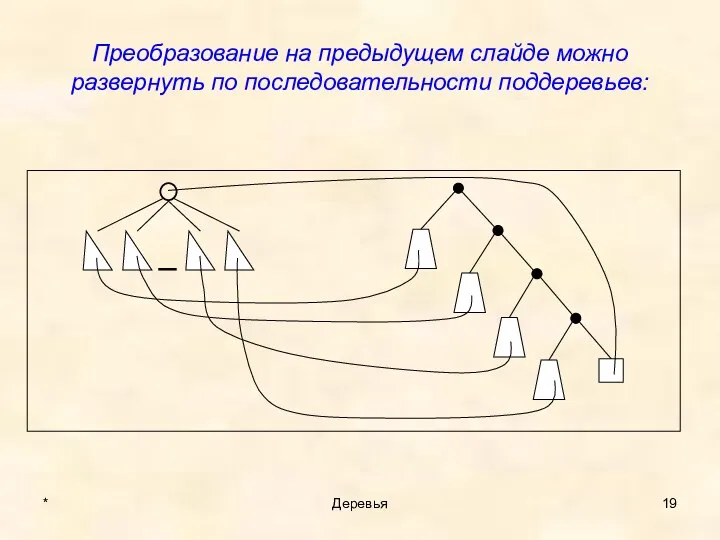
- 19. Преобразование на предыдущем слайде можно развернуть по последовательности поддеревьев: * Деревья
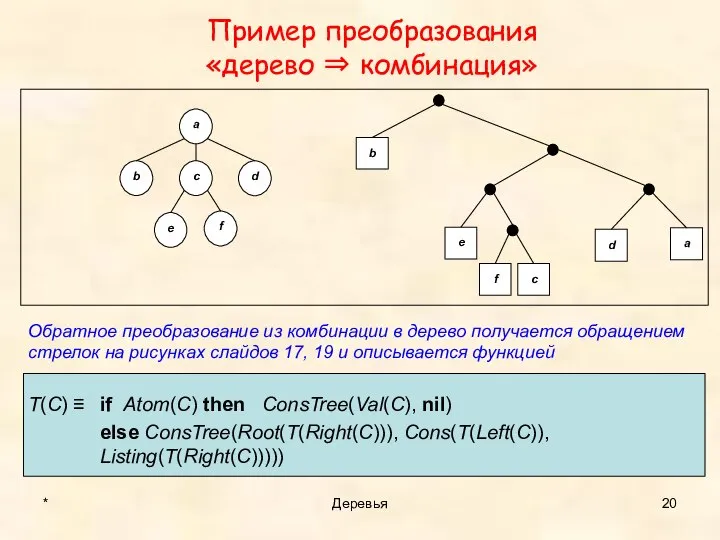
- 20. Обратное преобразование из комбинации в дерево получается обращением стрелок на рисунках слайдов 17, 19 и описывается
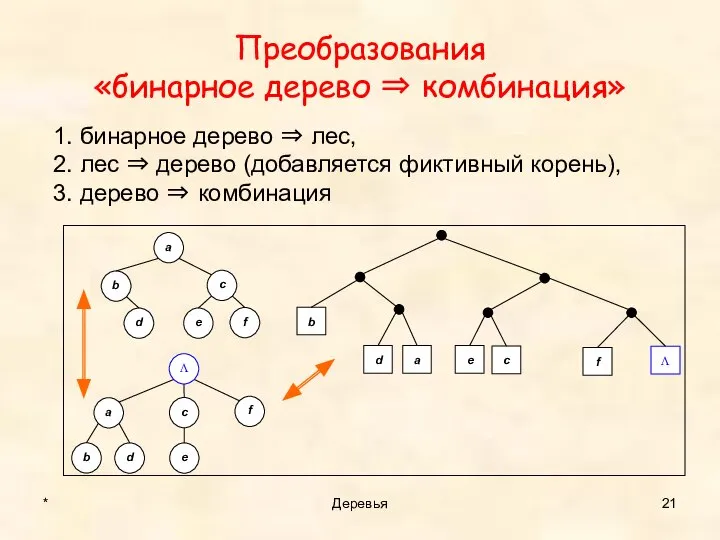
- 21. Преобразования «бинарное дерево ⇒ комбинация» * Деревья 1. бинарное дерево ⇒ лес, 2. лес ⇒ дерево
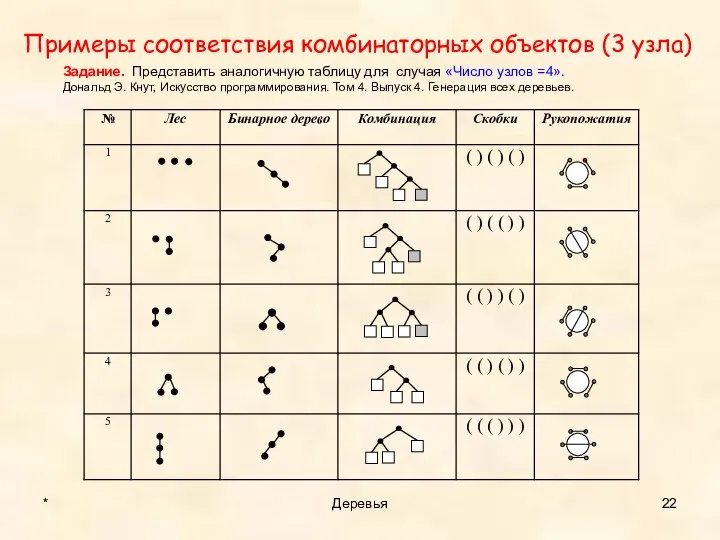
- 22. Примеры соответствия комбинаторных объектов (3 узла) * Деревья Задание. Представить аналогичную таблицу для случая «Число узлов
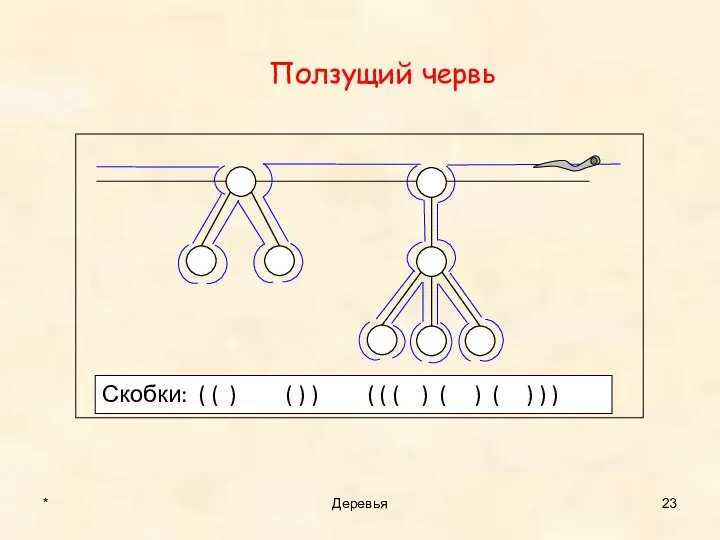
- 23. Ползущий червь * Деревья
- 25. Скачать презентацию











 Обработка графической информации.Тест
Обработка графической информации.Тест Школа Московской биржи. Иркутск, день 1
Школа Московской биржи. Иркутск, день 1 Массивы. Класс Array
Массивы. Класс Array Объяснение позиций игроков и очередь принятия решений
Объяснение позиций игроков и очередь принятия решений Arm builder. Создание docker-образа для компиляции программ и библиотек под arm архитектурой
Arm builder. Создание docker-образа для компиляции программ и библиотек под arm архитектурой Массивы
Массивы Защиты авторских прав в сети Internet
Защиты авторских прав в сети Internet Обработка изображения на шейдерах. Простейшая программа
Обработка изображения на шейдерах. Простейшая программа Понятия информации и системы счисления
Понятия информации и системы счисления Цифровые ресурсы
Цифровые ресурсы Role of Media in Social and Cultural Life
Role of Media in Social and Cultural Life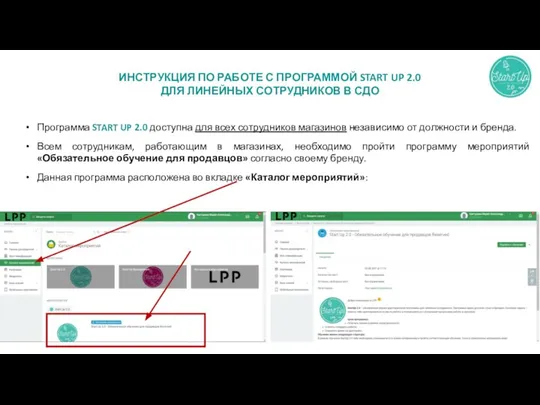 Инструкция по работе с программой start UP 2.0
Инструкция по работе с программой start UP 2.0 Дилер шмотом
Дилер шмотом Новая форма регистрации
Новая форма регистрации Организация ввода-вывода в Pascal
Организация ввода-вывода в Pascal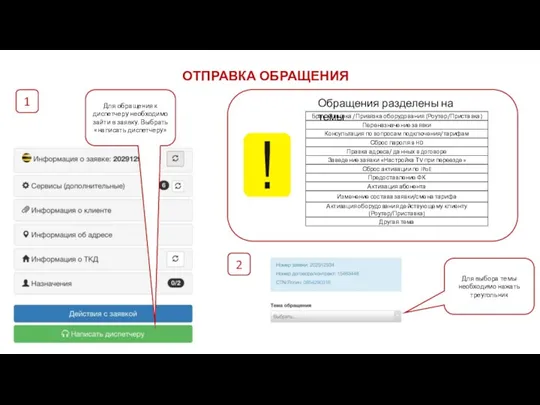 Отправка обращения
Отправка обращения Основные теоретические вопросы проектирования ПОР
Основные теоретические вопросы проектирования ПОР Информатика. Информационные технологии
Информатика. Информационные технологии Нормализация баз данных
Нормализация баз данных Анимация
Анимация Знаковые модели. Словесные модели Моделирование и формализация
Знаковые модели. Словесные модели Моделирование и формализация методы коммутации в ткс 17.09 (1)
методы коммутации в ткс 17.09 (1) Введение в компьютерные науки
Введение в компьютерные науки Технология мультимедиа
Технология мультимедиа Social media and pandemic
Social media and pandemic WordPress 6-7
WordPress 6-7 Цифровая управленческая платформа как способ оптимизации управленческих процессов в сфере обращения отходов производства
Цифровая управленческая платформа как способ оптимизации управленческих процессов в сфере обращения отходов производства Практика в СМЦ
Практика в СМЦ