Содержание
- 2. Кодирование и декодирование Для обмена информацией с другими людьми человек использует естественные языки. Наряду с естественными
- 3. Способы кодирования информации Для кодирования одной и той же информации могут быть использованы разные способы; их
- 4. Представление (кодирование) чисел
- 5. Двоичное кодирование в компьютере Вся информация, которую обрабатывает компьютер должна быть представлена двоичным кодом с помощью
- 6. Почему двоичное кодирование С точки зрения технической реализации использование двоичной системы счисления для кодирования информации оказалось
- 7. Система счисления Для записи информации о количестве объектов используются числа. Числа записываются с помощью набора специальных
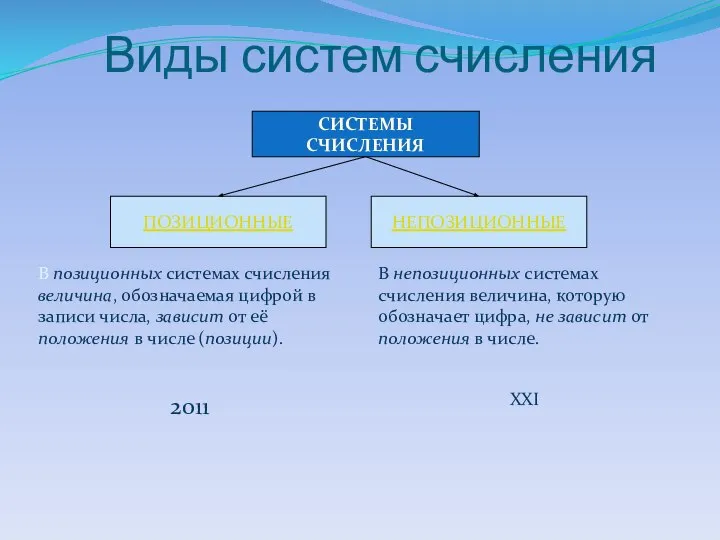
- 8. Виды систем счисления СИСТЕМЫ СЧИСЛЕНИЯ ПОЗИЦИОННЫЕ НЕПОЗИЦИОННЫЕ В непозиционных системах счисления величина, которую обозначает цифра, не
- 9. Непозиционные системы счисления Каноническим примером фактически непозиционной системы счисления является римская, в которой в качестве цифр
- 10. Древнеегипетская десятичная непозиционная система счисления. Примерно в третьем тысячелетии до нашей эры древние египтяне придумали свою
- 11. Алфавитные системы счисления. Более совершенными непозиционными системами счисления были алфавитные системы. К числу таких систем счисления
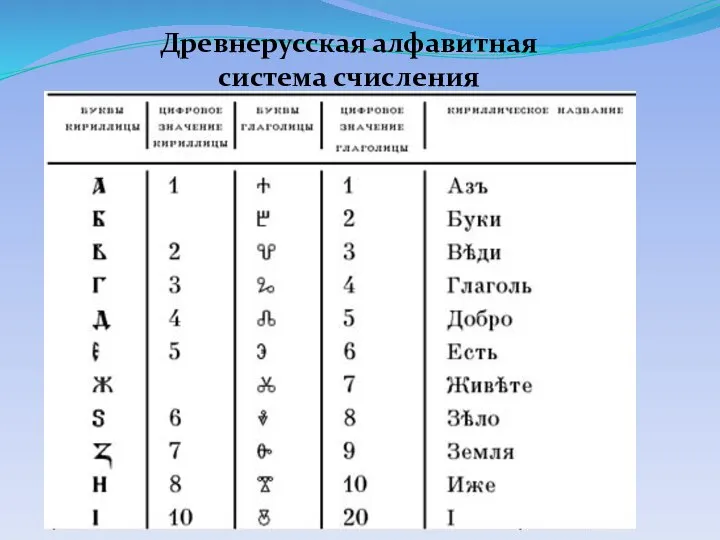
- 12. Древнерусская алфавитная система счисления
- 13. Позиционные системы счисления В позиционных системах счисления величина, обозначаемая цифрой в записи числа, зависит от её
- 14. Первые позиционные системы счисления Самой первой такой системой, когда счетным "прибором" служили пальцы рук, была пятеричная.
- 15. Двенадцатеричная система счисления Следующей после пятеричной возникла двенадцатеричная система счисления. Возникла она в древнем Шумере. Некоторые
- 16. Шестидесятеричная система счисления Следующая позиционная система счисления была придумана еще в Древнем Вавилоне, причем вавилонская нумерация
- 17. Какие позиционные системы счисления используются сейчас? В настоящее время наиболее распространены десятичная, двоичная, восьмеричная и шестнадцатеричная
- 18. Десятичная система счисления Десятичная система счисления — позиционная система счисления по основанию 10. Предполагается, что основание
- 19. Двоичная система счисления Двоичная система счисления — позиционная система счисления с основанием 2. Используются цифры 0
- 20. Алфавит десятичной, двоичной, восьмеричной и шестнадцатеричной систем счисления
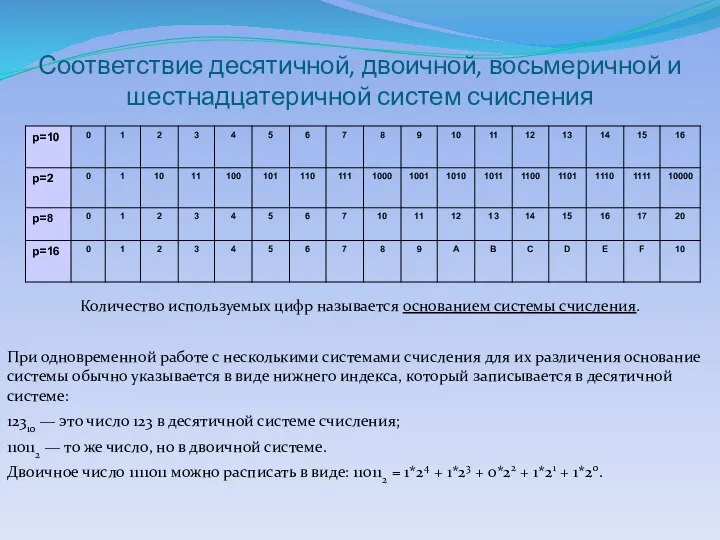
- 21. Соответствие десятичной, двоичной, восьмеричной и шестнадцатеричной систем счисления Количество используемых цифр называется основанием системы счисления. При
- 22. Перевод чисел из одной системы счисления в другую Перевод из десятичной системы счисления в систему счисления
- 23. Числа в компьютере Числа в компьютере хранятся и обрабатываются в двоичной системе счисления. Последовательность нулей и
- 24. Кодирование текстовой информации В традиционных кодировках для кодирования одного символа используется 8 бит. Легко подсчитать по
- 25. Кодирование текстовой информации От начала 90-ых годов, времени господства операционной системы MS DOS, остается кодировка CP866.
- 26. Кодирование текстовой информации Последовательности десятичных кодов слова «ЭВМ» в различных кодировках составляем на основе кодировочных таблиц:
- 27. Международная кодировка ASCII
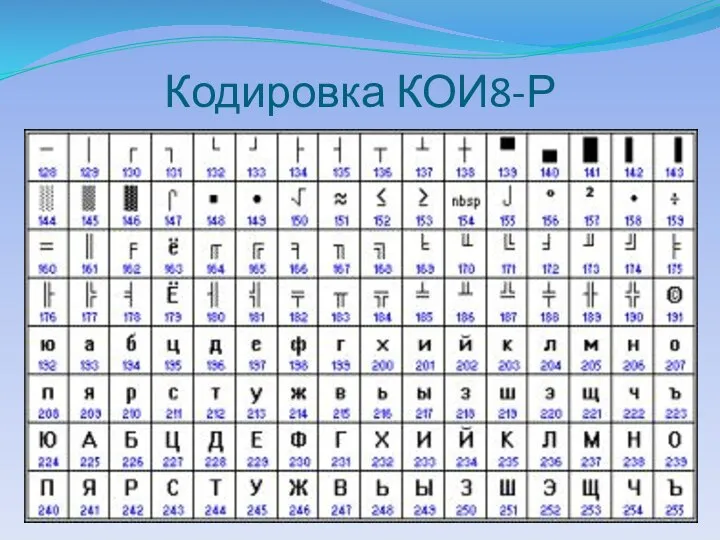
- 28. Кодировка КОИ8-Р
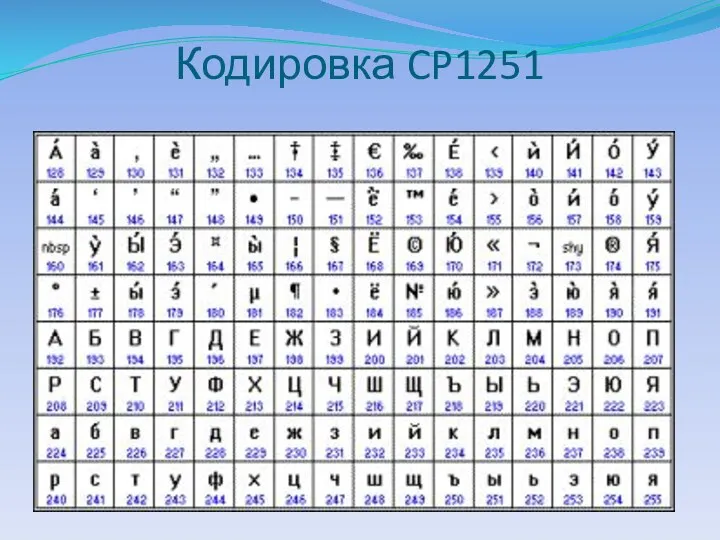
- 29. Кодировка CP1251
- 30. Представление видеоинформации В последнее время компьютер все чаще используется для работы с видеоинформацией. Простейшей такой работой
- 31. Представление видеоинформации Казалось бы, если проблемы кодирования статической графики и звука решены, то сохранить видеоизображение уже
- 32. Некоторые форматы видеофайлов Существует множество различных форматов представления видеоданных. В среде Windows, например, уже более 10
- 33. Мультимедиа Мультимедиа (multimedia, от англ. multi - много и media - носитель, среда) - совокупность компьютерных
- 35. Скачать презентацию



























 Особенности защиты информации в компьютерных сетях
Особенности защиты информации в компьютерных сетях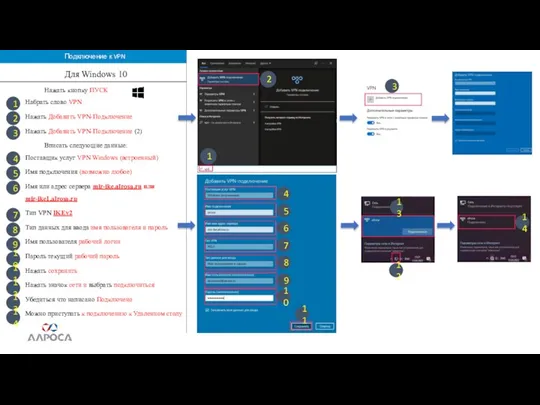 Подключение к VPN Для Windows 10
Подключение к VPN Для Windows 10 Новий INVASION REVOLT RS
Новий INVASION REVOLT RS Сервисы для создания дидактических материалов
Сервисы для создания дидактических материалов WinAPI Графика - относительные координаты. Функции с параметрами
WinAPI Графика - относительные координаты. Функции с параметрами Троллинг
Троллинг Язык программирования Python
Язык программирования Python Алгоритм. Свойства алгоритма
Алгоритм. Свойства алгоритма Кибернетические системы
Кибернетические системы Віруси та антивіруси
Віруси та антивіруси Системы распознавания речи: базовые принципы и алгоритмы
Системы распознавания речи: базовые принципы и алгоритмы I mobili di Jerry
I mobili di Jerry Контент-анализ онлайн-ресурсов, посвященных тенденциям развития отраслей инновационных проектов
Контент-анализ онлайн-ресурсов, посвященных тенденциям развития отраслей инновационных проектов Хеширование паролей. Лекция №6
Хеширование паролей. Лекция №6 Состав компьютера
Состав компьютера Искусственный интеллект. Модели, проектирование, разработка
Искусственный интеллект. Модели, проектирование, разработка Моделирование эпидемии гриппа
Моделирование эпидемии гриппа Создание таблиц баз данных. Задание
Создание таблиц баз данных. Задание Логические элементы
Логические элементы Разработка веб-сервиса для обработки снимков ДЗЗ
Разработка веб-сервиса для обработки снимков ДЗЗ Спецсимволы
Спецсимволы Компьютерное моделирование работы ядерного реактора
Компьютерное моделирование работы ядерного реактора Мовиус — это система автоматической продажи билетов в соответствии с ФЗ-54
Мовиус — это система автоматической продажи билетов в соответствии с ФЗ-54 Электронные таблицы EXCEL
Электронные таблицы EXCEL Умозаключение (4 класс)
Умозаключение (4 класс) Datortikli
Datortikli Защита информации в компьютерных системах
Защита информации в компьютерных системах Аутентификация и идентификация. Программно-технические способы реализации идентификации и аутентификации
Аутентификация и идентификация. Программно-технические способы реализации идентификации и аутентификации