Содержание
- 2. Структуры данных Структуры данных Составитель курса лекций: Спиричева Наталия Рахматулловна, ст. преподаватель каф. Информационных технологий
- 3. Структуры данных Структуры данных Древовидные структуры данных
- 4. Структуры данных Структуры данных и алгоритмы Целью лекции является приобретение студентами следующих компетенций: знать методы представления
- 5. Структуры данных Структуры данных и алгоритмы Основные темы лекции: Понятие древовидных структур Деревья Графы Алгоритмы поиска
- 6. Структуры данных Введение Дерево - конечное множество, состоящее из одного или более элементов, называемых узлами. Корень
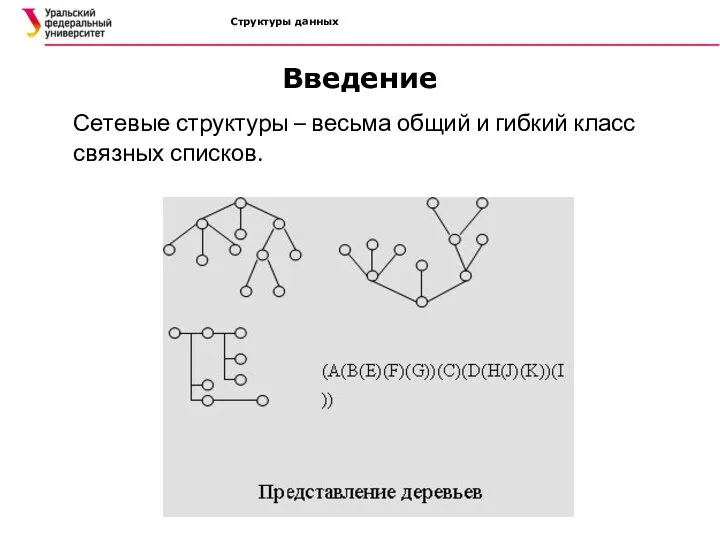
- 7. Структуры данных Введение Сетевые структуры – весьма общий и гибкий класс связных списков.
- 8. Структуры данных Введение Определим дерево как конечное множество Т, состоящее из одного или более узлов, таких,
- 9. Структуры данных Из определения следует: Каждый узел дерева является корнем некоторого поддерева, которое содержится в этом
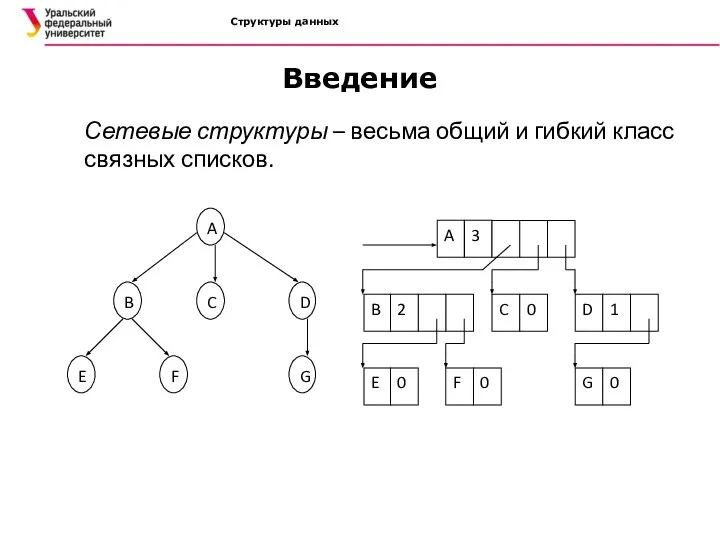
- 10. Структуры данных Введение Обычно дерево представляется в машинной памяти в форме многосвязного списка, в котором каждый
- 11. Структуры данных Введение Сетевые структуры – весьма общий и гибкий класс связных списков.
- 12. Структуры данных Введение Лес – это множество (обычно упорядоченное), состоящее из некоторого (быть может равного нулю)
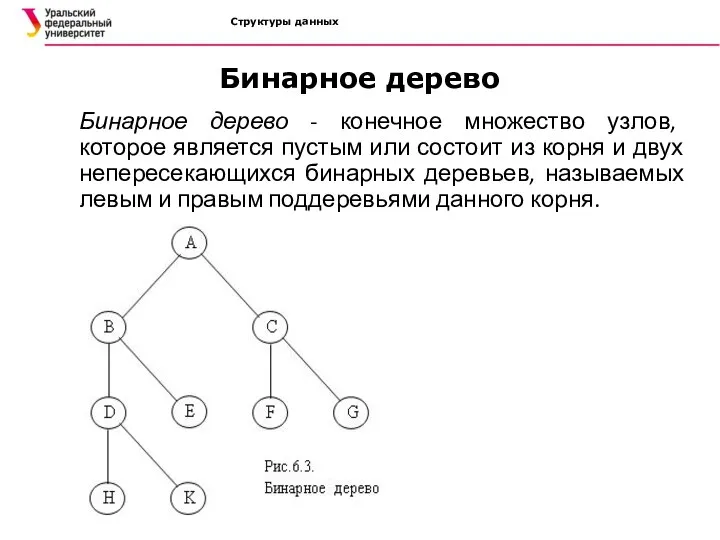
- 13. Структуры данных Бинарное дерево Бинарное дерево - конечное множество узлов, которое является пустым или состоит из
- 14. Структуры данных Бинарное дерево В алгоритмах работы с древовидными структурами наиболее часто встречается понятие обход дерева.
- 15. Структуры данных Бинарное дерево Прямой порядок обхода: Попасть в корень Пройти левое поддерево Пройти правое поддерево
- 16. Структуры данных Бинарное дерево “Прошитые” деревья В “прошитых” деревьях концевые связи-указатели используются для связи с родителями,
- 17. Структуры данных Деревья Графы
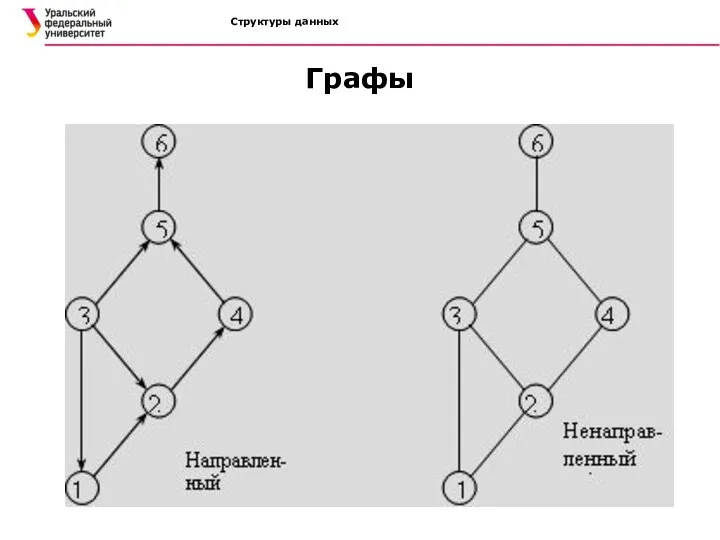
- 18. Структуры данных Графы Граф - некоторое множество точек (называемых вершинами) и некоторое множество линий (называемых ребрами),
- 19. Структуры данных Графы Каждая пара вершин в графе соединяется не больше чем одним ребром. Дуга, соединенная
- 20. Структуры данных Графы Пусть V и V` - вершины и пусть n≥0; говорят, что «V0, V1,
- 21. Структуры данных Графы Граф называется связным, если имеется путь между каждыми двумя вершинами этого графа. Циклом
- 22. Структуры данных Графы
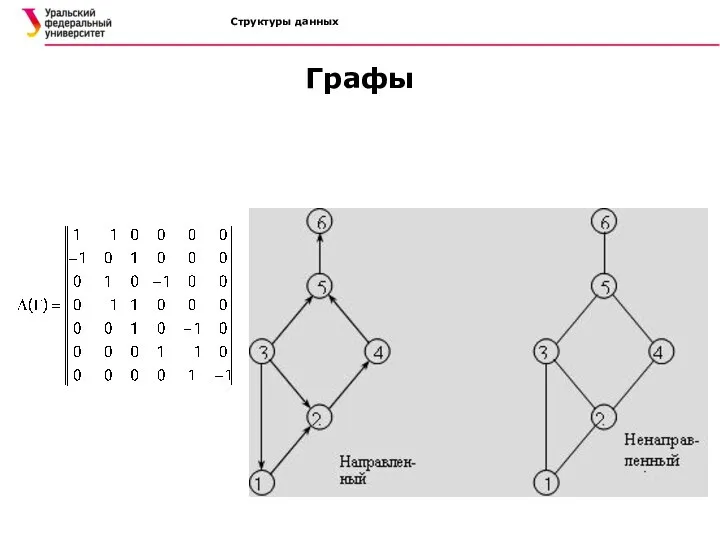
- 23. Структуры данных Графы Задание графа: Класс матриц инциденции. Если граф Г содержит n вершин и m
- 24. Структуры данных Графы
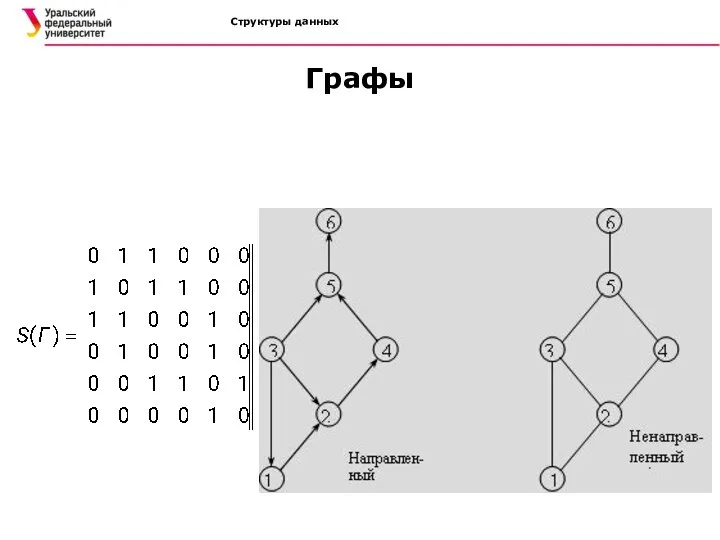
- 25. Структуры данных Графы Класс матриц смежности. Матрица смежности S=[sij]nxm невзвешенного графа определяется следующим образом: Во взвешенном
- 26. Структуры данных Графы
- 27. Структуры данных Деревья Алгоритмы поиска путей в графе
- 28. Структуры данных Алгоритмы поиска путей в графе Путь с минимальным количеством промежуточных вершин Алгоритм просматривает вершины
- 29. Структуры данных Волновой алгоритм Каждой вершине i приписывается два целых числа Times[i] - временная метка и
- 30. Структуры данных Под корректностью алгоритма здесь понимается, что: алгоритм завершает работу за конечное время; если решение
- 31. Структуры данных Алгоритмы поиска путей в графе Путь минимальной суммарной длины во взвешенном графе с неотрицательными
- 32. Структуры данных Алгоритмы поиска путей в графе Алгоритм, по которому происходит поиск, заключается в следующем: всем
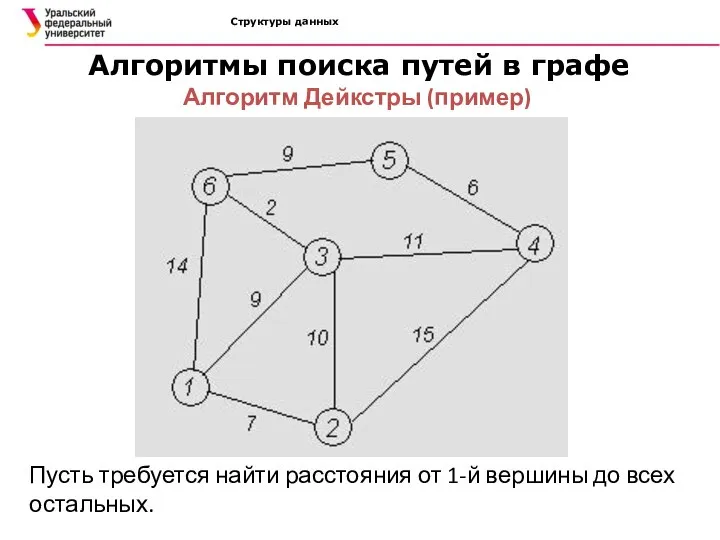
- 33. Структуры данных Алгоритмы поиска путей в графе Алгоритм Дейкстры (пример) Пусть требуется найти расстояния от 1-й
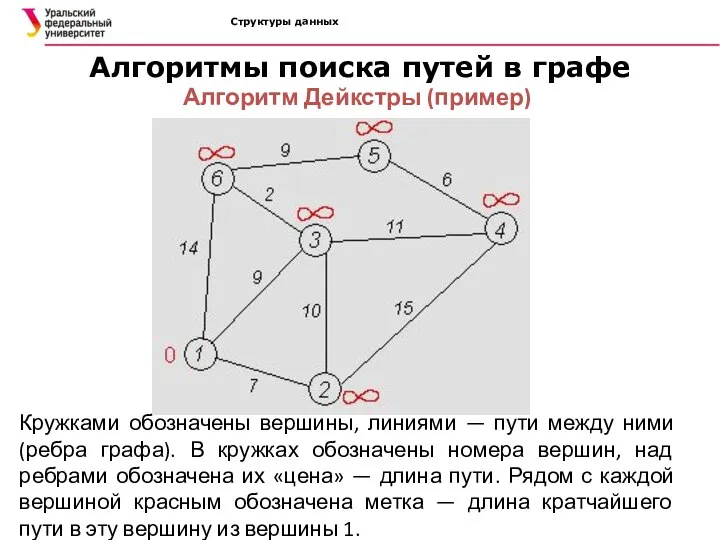
- 34. Структуры данных Алгоритмы поиска путей в графе Алгоритм Дейкстры (пример) Кружками обозначены вершины, линиями — пути
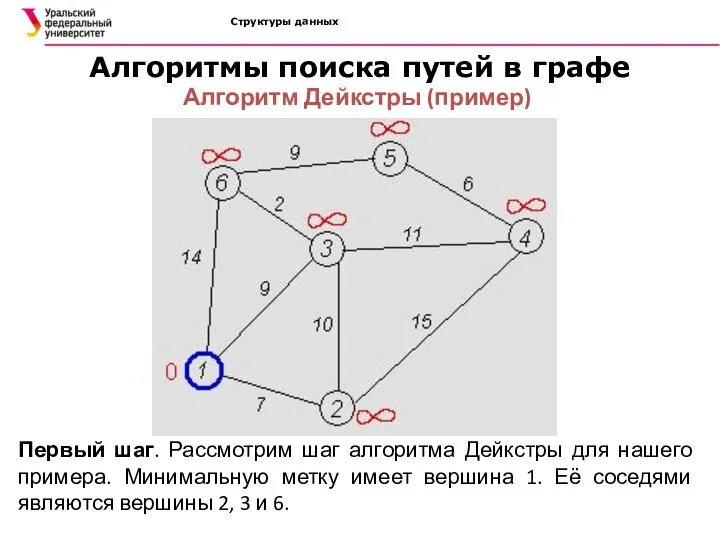
- 35. Структуры данных Алгоритмы поиска путей в графе Алгоритм Дейкстры (пример) Первый шаг. Рассмотрим шаг алгоритма Дейкстры
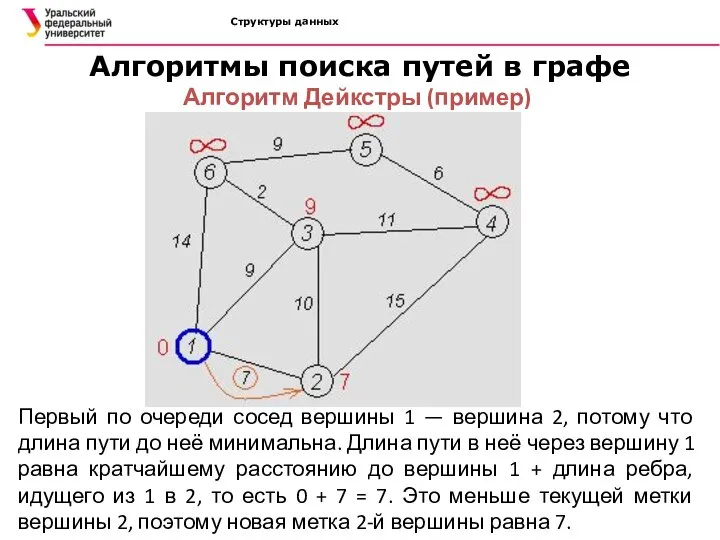
- 36. Структуры данных Алгоритмы поиска путей в графе Алгоритм Дейкстры (пример) Первый по очереди сосед вершины 1
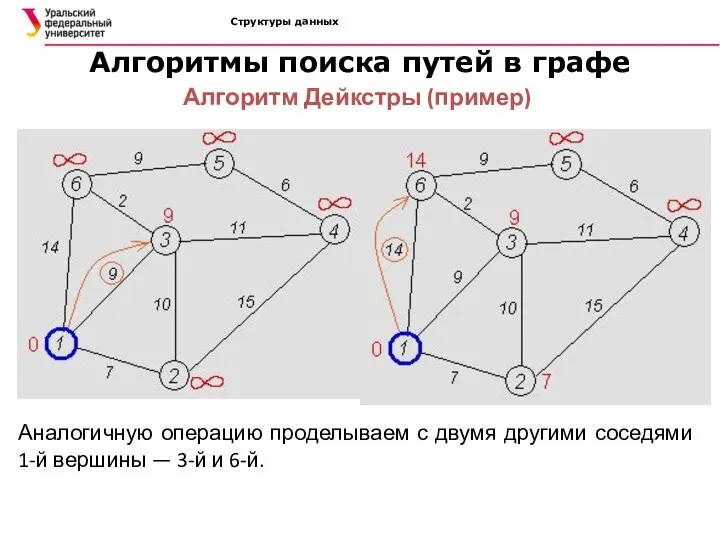
- 37. Структуры данных Алгоритмы поиска путей в графе Алгоритм Дейкстры (пример) Аналогичную операцию проделываем с двумя другими
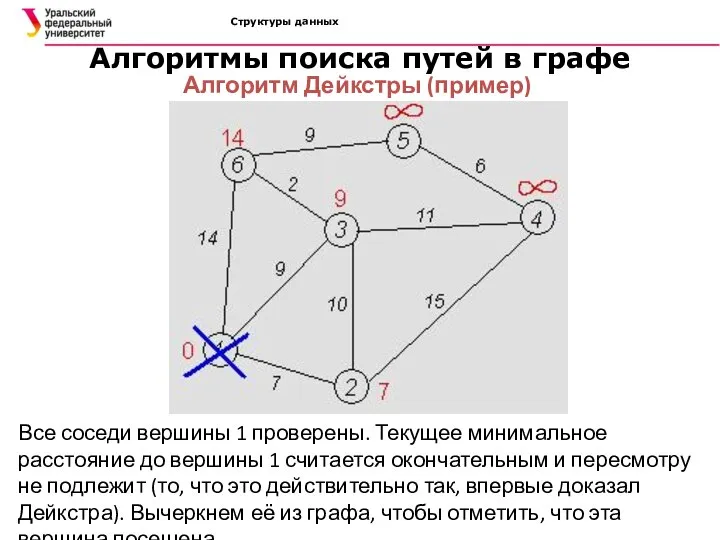
- 38. Структуры данных Алгоритмы поиска путей в графе Алгоритм Дейкстры (пример) Все соседи вершины 1 проверены. Текущее
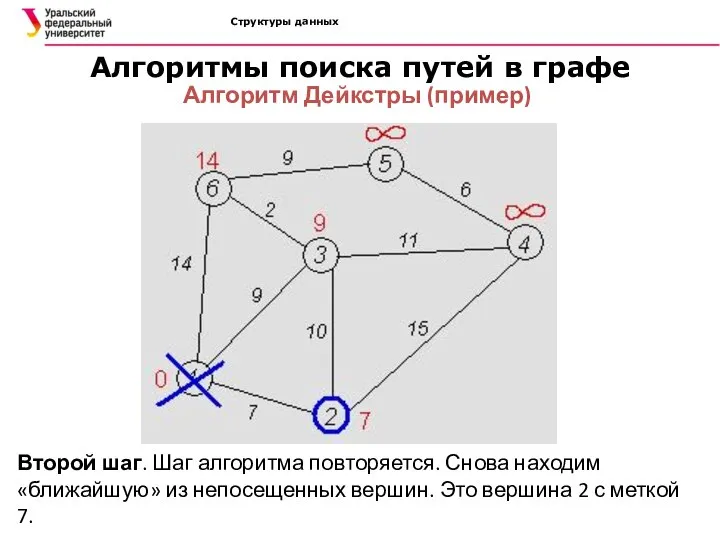
- 39. Структуры данных Алгоритмы поиска путей в графе Алгоритм Дейкстры (пример) Второй шаг. Шаг алгоритма повторяется. Снова
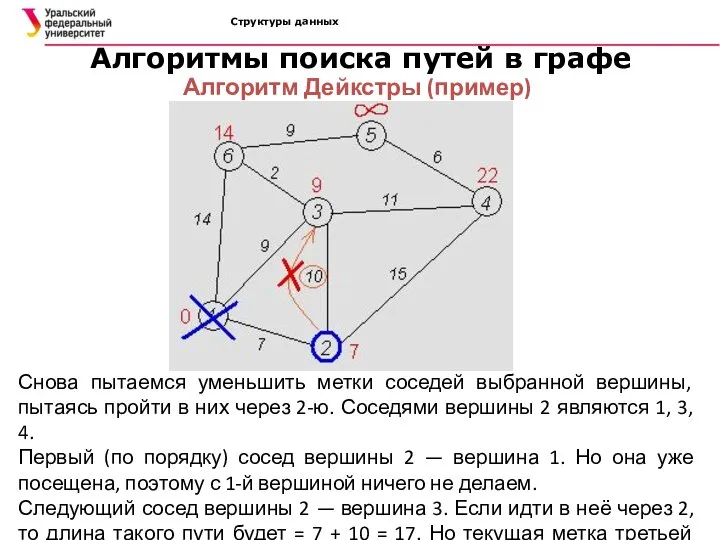
- 40. Структуры данных Алгоритмы поиска путей в графе Алгоритм Дейкстры (пример) Снова пытаемся уменьшить метки соседей выбранной
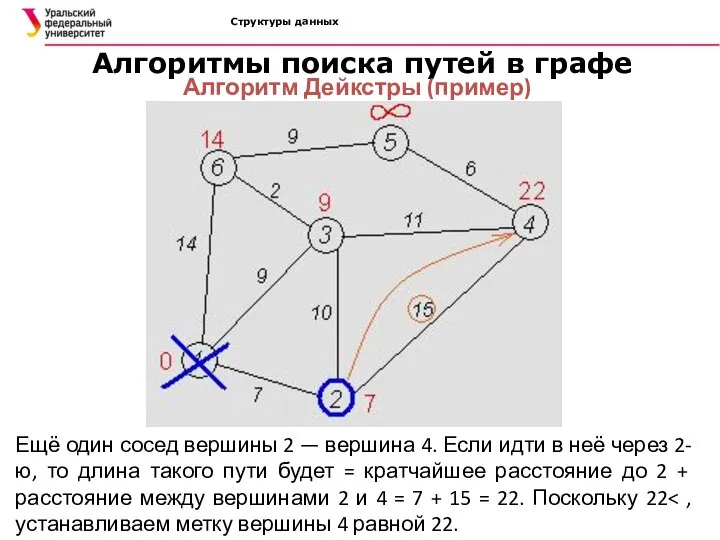
- 41. Структуры данных Алгоритмы поиска путей в графе Алгоритм Дейкстры (пример) Ещё один сосед вершины 2 —
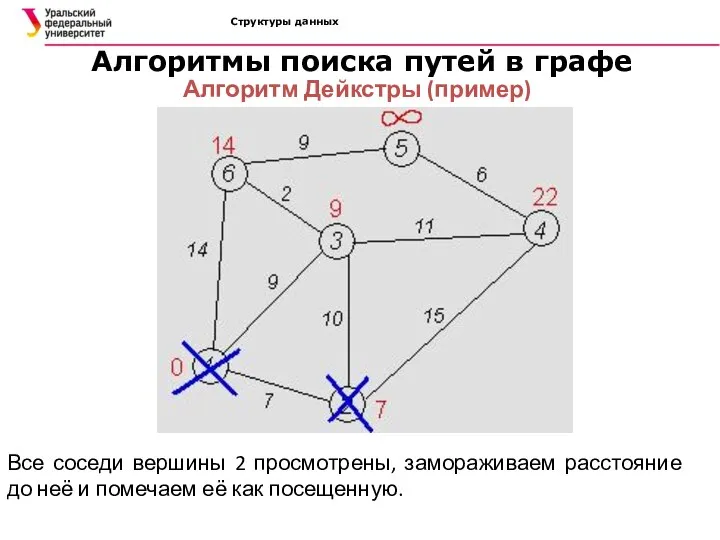
- 42. Структуры данных Алгоритмы поиска путей в графе Алгоритм Дейкстры (пример) Все соседи вершины 2 просмотрены, замораживаем
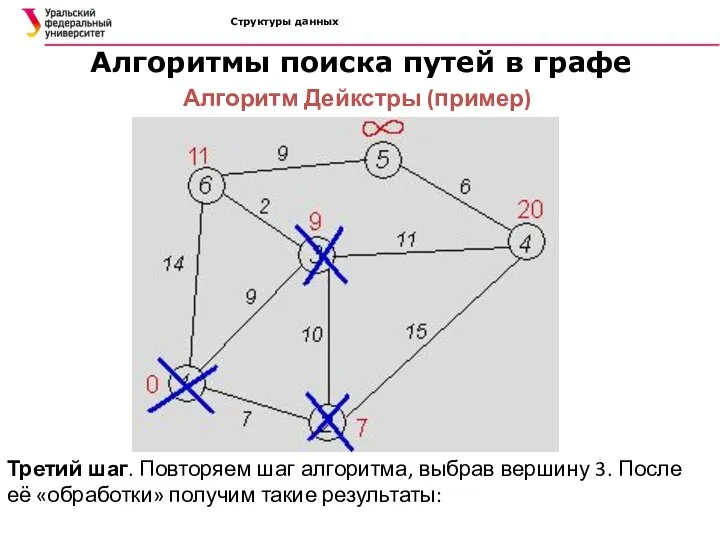
- 43. Структуры данных Алгоритмы поиска путей в графе Алгоритм Дейкстры (пример) Третий шаг. Повторяем шаг алгоритма, выбрав
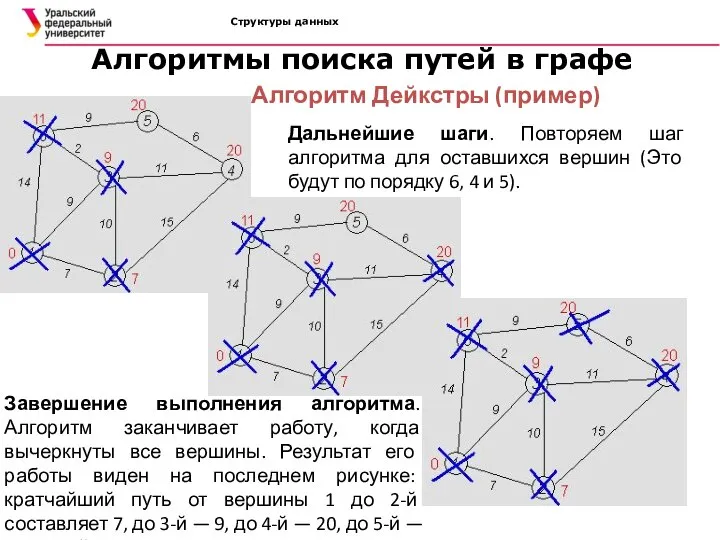
- 44. Структуры данных Алгоритмы поиска путей в графе Алгоритм Дейкстры (пример) Дальнейшие шаги. Повторяем шаг алгоритма для
- 45. Структуры данных Алгоритмы поиска путей в графе Путь минимальной суммарной длины во взвешенном графе с произвольными
- 46. Структуры данных Алгоритмы поиска путей в графе Нахождение K путей минимальной суммарной длины во взвешенном графе
- 47. Структуры данных Алгоритмы поиска путей в графе Алгоритм: 1. Найти минимальный путь P1=(v11,...,v1L[1]). Положить k =
- 48. Структуры данных 1.Какими структурами данных можно представить в памяти древовидные структуры? 2. Перечислите основные алгоритмы поиска
- 50. Скачать презентацию


















![Структуры данных Графы Класс матриц смежности. Матрица смежности S=[sij]nxm невзвешенного графа определяется](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/986754/slide-24.jpg)


![Структуры данных Волновой алгоритм Каждой вершине i приписывается два целых числа Times[i]](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/986754/slide-28.jpg)







 Операционные системы: безопасность. Основы безопасности
Операционные системы: безопасность. Основы безопасности Разработка программных средств обеспечения грузоперевозок
Разработка программных средств обеспечения грузоперевозок Oracle Solaris
Oracle Solaris Форматирование графических изображений в Microsoft office
Форматирование графических изображений в Microsoft office Microsoft Excel. Условное форматирование
Microsoft Excel. Условное форматирование Microsoft Office. Краткая характеристика изученных программ
Microsoft Office. Краткая характеристика изученных программ Файлы и файловые структуры
Файлы и файловые структуры Многозадачная операционная система Unix
Многозадачная операционная система Unix Dependability systemów 7. Redundancja
Dependability systemów 7. Redundancja Что такое компьютер
Что такое компьютер Единый урок по безопасности в сети Интернет (сентябрь-ноябрь 2018)
Единый урок по безопасности в сети Интернет (сентябрь-ноябрь 2018) Введение в профессию web - разработчика
Введение в профессию web - разработчика Установка 1С - Битрикс
Установка 1С - Битрикс История развития интернета, цель и основа ее создания
История развития интернета, цель и основа ее создания С чего начать в IT
С чего начать в IT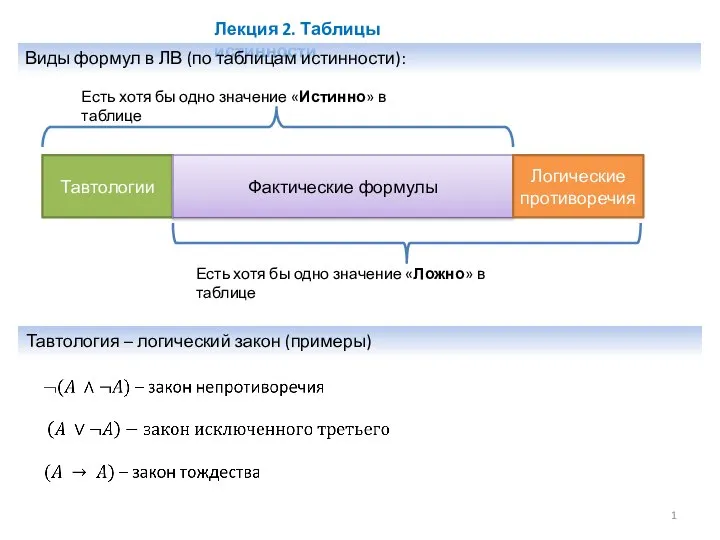 Таблицы истинности
Таблицы истинности Графический редактор Paint. Рисуем Велосипед
Графический редактор Paint. Рисуем Велосипед БЭСТ-5. Мой бизнес
БЭСТ-5. Мой бизнес Информационное сопровождение деятельности органов государственного и муниципального управления Российской Федерации
Информационное сопровождение деятельности органов государственного и муниципального управления Российской Федерации Анализ данных
Анализ данных Электронно-цифровая подпись
Электронно-цифровая подпись Введение в архитектуру ЭВМ
Введение в архитектуру ЭВМ Распределение функциональных требований безопасности
Распределение функциональных требований безопасности Алгоритмы
Алгоритмы Autodesk inventor. Работа в режиме модель. Конструкционные операции. Стратегия построения
Autodesk inventor. Работа в режиме модель. Конструкционные операции. Стратегия построения Стандарты защиты
Стандарты защиты Телеком24
Телеком24 Формирование сведений об объекте закупке – лекарственном препарате в составе информации о контракте
Формирование сведений об объекте закупке – лекарственном препарате в составе информации о контракте