Другие системы счисления. Троичная уравновешенная система счисления. Двоично-десятичная система счисления

Задача Баше о наборе гирь
+ 1 гиря на правой чашке
0 гиря снята
– 1 гиря на левой чашке
Как с помощью 4-х гирь взвесить от 0 до 40 кг?
Веса гирь – степени числа 3:
1 кг, 3 кг, 9 кг, 27 кг
Пример:
27 кг + 9 кг + 3 кг + 1 кг = 40 кг

Троичная уравновешенная система
ЭВМ «Сетунь» (1958) , Н.П. Брусенцов
Основание: 3
Алфавит: («-1»), 0, 1
Для N разрядов: всего 3N значений:
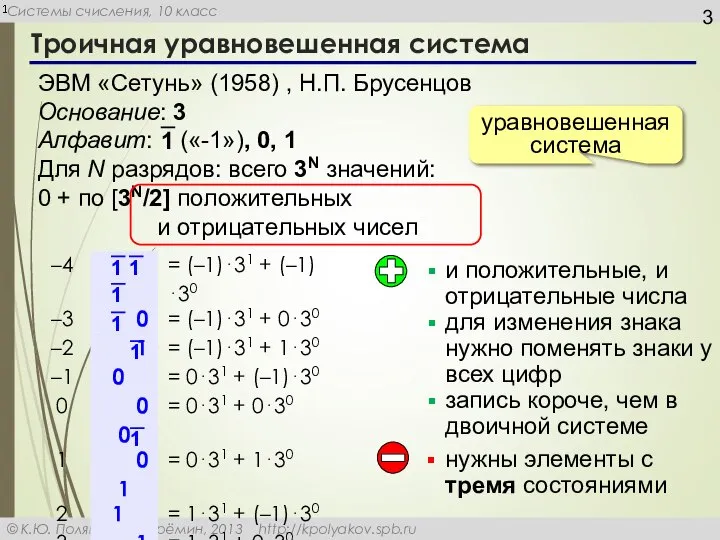
0 + по [3N/2] положительных и отрицательных чисел
уравновешенная система
и положительные, и отрицательные числа
для изменения знака нужно поменять знаки у всех цифр
запись короче, чем в двоичной системе
нужны элементы с тремя состояниями

Двоично-десятичная система (ДДС)
Десятичные цифры, закодированные в двоичном коде. Вinary coded decimal (BCD).
9024,19 = 1001 0000 0010 0100, 0001 1001ДДС
9 0 2 4 1 9
101010011,01111ДДС =
= 0001 0101 0011, 0111 1000ДДС = 153,78
легко переводить в десятичную систему
просто умножать и делить на 10
конечные десятичные дроби записываются точно (аналог ручных расчётов)
длиннее, чем двоичная запись
сложнее арифметические операции
Использование – в калькуляторах.

Другие нетрадиционный системы счисления
Рассмотрим еще две нетрадиционные системы счисления.
Первая называется факториальной.
В этой системе счисления базис образует последовательность факториалов натуральных чисел: 1!=1, 2!=1*2=2, 3! =1*2*3=6, 4!=1*2*3*4=24, 5!=1*2*3*4*5=120, 6!=1*2*3*4*5*6=720 и т.д.
Другой ее особенностью является то, что количество цифр, используемых в том или ином разряде (так называемая размерность алфавита), неодинаково — оно увеличивается с ростом номера разряда. В первом разряде могут быть только цифры 0 и 1, во втором — 0, 1 и 2, в k-м — 0, 1, 2, …, k и так далее. Следовательно, если запись числа в факториальной системе имеет вид dn dn–1…d2d1, то этому числу соответствует десятичное значение, равное
= d1 · 1! + d2 · 2! + d3 · 3! + … + dn · n!,
где dk — цифра числа (0 dk k).
Десятичному же числу 2008 соответствует
2 · 720 + 4 · 120 + 3 · 24 + 2 · 6 + 2 · 2 + 0 · 1 = 2 · 6! + 4 · 5! + 3 · 4! + 2 · 3! +
+ 2 · 2! + 0 · 1! = 243220f (буква f в виде индекса говорит о записи числа в факториальной системе).

Задача№1
Переведите числа из десятичной системы счисления в факториальную :
Рассмотрим решение задачи
ЗНАЕМ 1!=1, 2!=2, 3! =6, 4!=24, 5!=120
Записать десятичное число в факториальной системе значит представить его в виде последовательности:
dn · n! +…d3 · 3! +d2 · 2!+ d1 · 1! ,
Т.к. 4! < 91 < 5!, то n=4
Следовательно, 91= d4 · 4! +d3 · 3! +d2 · 2!+ d1 · 1! =dn · 24 +d3 · 6 +d2 · 2+ d1 · 1 ,
А теперь найдем коэффициенты
Сколько раз число 24 содержится в числе 91? d4 =91 div 24=3 (деление нацело)
Что останется? 91 mod 24=19 (остаток от деления нацело) 91-24*3=19
Теперь анализируем число 19?
Сколько раз число 19 содержит 6 (3!)? d3 = 19 div 6=3
Что останется? 19 mod 6 =1
Понятно, что d2=0 ( т.к 1<2!), а d1=1
Таким образом, 91= 3 · 4! +3 · 3! +0 · 2!+ 1 · 1!=3301f
Ответ: 3301f

Задача №2
Переведите в десятичную систему числа, записанные в факториальной системе
Рассмотрим решение задачи
ЗНАЕМ 1!=1, 2!=2, 3! =6, 4!=24, 5!=120
Перевести число из факториальной системы в десятичную значит подсчитать значениие многочлена:
dn · n! +…d3 · 3! +d2 · 2!+ d1 · 1! ,
В числе 2121f четыре цифры, значит
2121f= 2*4! + 1*3! + 2*2! + 1*1! = 2*24 + 1*6 + 2*2 + 1*1= 5910
ОТВЕТ: 5910

Другие нетрадиционный системы счисления
Фибоначчиева система счисления известна еще более узкому кругу специалистов. Из названия нетрудно догадаться, что она основывается на числах Фибоначчи. В этой системе счисления вес k-го разряда равен k-му числу Фибоначчи (каждый член, начиная с третьего, равен сумме двух предыдущих):
1, 2, 3, 5, 8, 13, 21, 34, 55, …
Используемые цифры (алфавит) — только 0 и 1. Следовательно, если запись числа в фибоначчиевой системе имеет вид fn fn–1…f2f1, то этому числу соответствует десятичное значение, равное , где Fk — числа Фибоначчи, fk {0, 1}, причем в записи числа две единицы не должны стоять рядом1. Последнее замечание крайне важно: при несоблюдении этого условия запись числа будет неоднозначной. Например, число 510 может быть записано как
110Fib (5 = 1 · 3 + 1 · 2 + 0 · 1) и
1000Fib (5 = 1 · 5 + 0 · 3 + 0 · 2 + 0 · 1),
но правильным считается второе число, где в записи нет двух подряд идущих единиц. В этом случае каждое натуральное число в фибоначчиевой системе счисления записывается единственным образом. Например, 200810 = 1597 + 377 + 34 = F16 + F13 + F8 = 1001000010000000Fib.
Необходимо отметить, что, хотя для записи числа в этой системе счисления используются только цифры 0 и 1, эту запись нельзя считать двоичным представлением числа.