ЕГЭ. Информатика, задание 1

Системы счисления и операции над числами в разных системах счисления
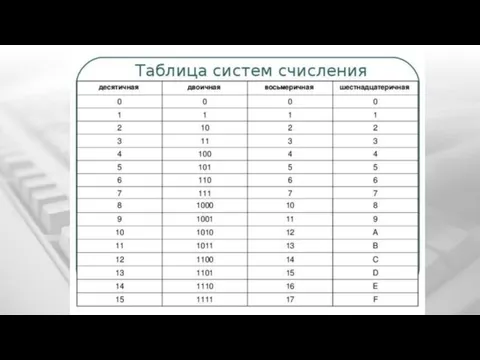
Система счисления — это совокупность правил записи чисел посредством конечного набора символов (цифр).
Системы счисления бывают:
непозиционными (в этих системах значение цифры не зависит от ее позиции — положения в записи числа);
позиционными (значение цифры зависит от позиции).
Непозиционная — самая древняя, в ней каждая цифра числа имеет величину, не зависящую от её позиции (разряда). То есть, если у вас 5 черточек — то число тоже равно 5, поскольку каждой черточке, независимо от её места в строке, соответствует всего 1 один предмет.
Позиционная система — значение каждой цифры зависит от её позиции (разряда) в числе. Например, привычная для нас 10-я система счисления — позиционная. Рассмотрим число 453. Цифра 4 обозначает количество сотен и соответствует числу 400, 5 — кол-во десяток и аналогично значению 50, а 3 — единиц и значению 3. Как видим — чем больше разряд — тем значение выше. Итоговое число можно представить, как сумму 400+50+3=453.

Перевод чисел из 10-й системы счисления в двоичную:

Перевод чисел из 2-й системы счисления в 10-ую

При работе с большими числами, лучше использовать разложение по степеням двойки:

Перевод чисел из 10-й системы счисления в 8-ую

Перевод чисел из 8-й сист. сч-я в 10-ую

Перевод чисел из 8-й сист. сч-я в 2-ую и обратно триадами

Перевод чисел из 10-й системы счисления в 16-ую

Перевод из 16-й системы счисления в 10-ую

Перевод чисел из 2-й сист. сч-я в 16-ую и обратно тетрадами

ПОЛЕЗНОСТИ ДЛЯ ДВОИЧНОЙ СИСТЕМЫ СЧИСЛЕНИЯ:
числа, которые в 2-ной системе счисления оканчиваются на 0 — четные, на 1 — нечетные;
соответственно, числа, которые делятся на 4, будут оканчиваться на 00, и т.д.; таким образом, выведем общее правило:числа, которые делятся на 2k, оканчиваются на k нулей
если число N находится в интервале 2k-1 ≤ N < 2k, в его двоичной записи будет ровно kцифр, например, для 126:26 = 64 ≤ 126 < 128 = 27, 126 = 11111102 (7 цифр)
если число имеет вид 2k, то оно записывается в двоичной системе как единица и kнулей, например:32 = 25 = 1000002
если число имеет вид 2k-1, то оно записывается в двоичной системе k единиц, например:31 = 25-1 = 111112
если известна двоичная запись N, то двоичную запись числа 2•N можно легко получить, приписав в конец ноль, например:15 = 11112, 30 = 111102, 60 = 1111002, 120 = 11110002
Необходимо также выучить степени двойки, увеличивая степень справа налево:1024 512 256 128 64 32 16 8 4 2 1 210 29 28 27 26 25 24 23 22 21 20
желательно выучить таблицу двоичного представления цифр от 0 до 7 в виде триад (групп из 3-х битов)

Выполнение заданий