Содержание
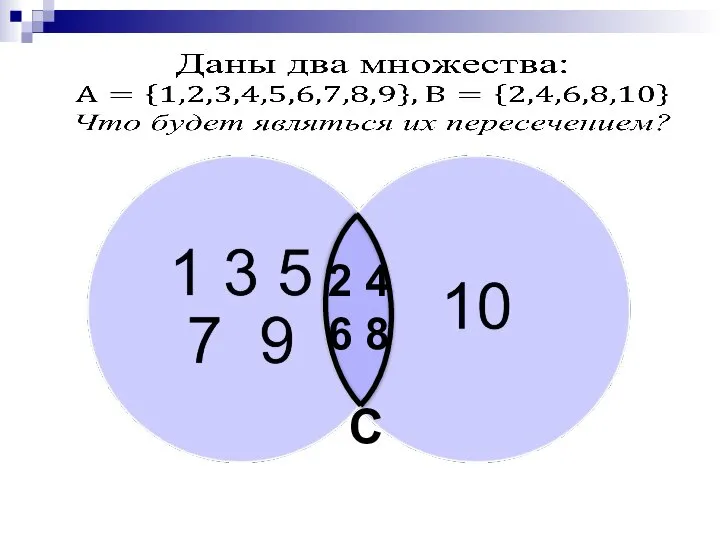
- 2. 2 4 6 8 С
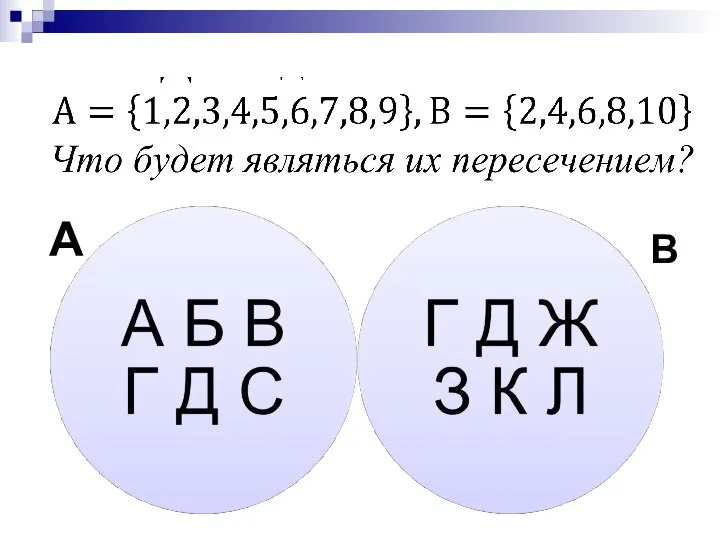
- 3. А В
- 4. С
- 5. Ребус
- 6. Алгебра - наука об общих операциях, аналогичных сложению и умножению, которые могут выполняться над различными математическими
- 7. Алгебра логики отвлекается от смысловой содержательности высказываний. Ее интересует только один факт — истинно или ложно
- 8. Элементы алгебры логики
- 9. Высказывание - это предложение на любом языке, содержание которого можно однозначно определить как истинное или ложное.
- 10. В русском языке высказывания выражаются повествовательными предложениями: Январь – зимний месяц. Москва – столица России. Приведите
- 11. Побудительные и вопросительные предложения высказываниями не являются. Как красив закат! Войдите в класс. Ты выучил стихотворение?
- 13. Высказывание называется простым, если никакая его часть сама не является высказыванием. Сложные (составные) высказывания строятся из
- 14. Простые высказывания в алгебре логики обозначаются заглавными латинскими буквами: А = {Аристотель - основоположник логики} В
- 15. Логические операции задаются таблицами истинности и могут быть графически проиллюстрированы с помощью диаграмм Эйлера-Венна.
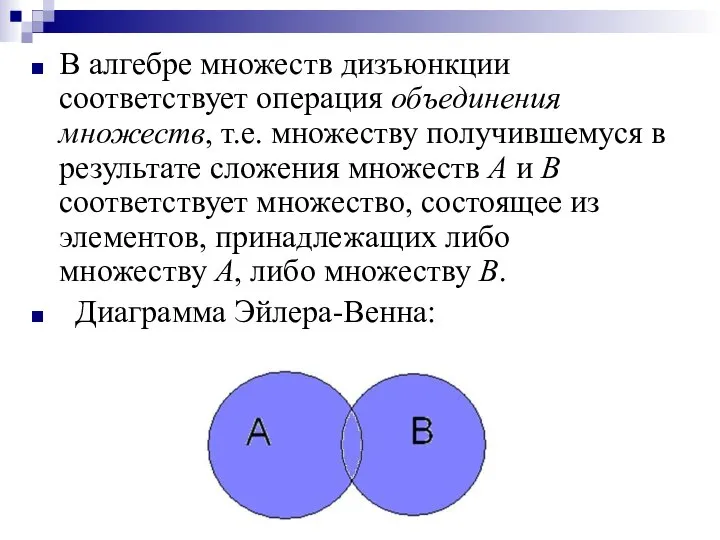
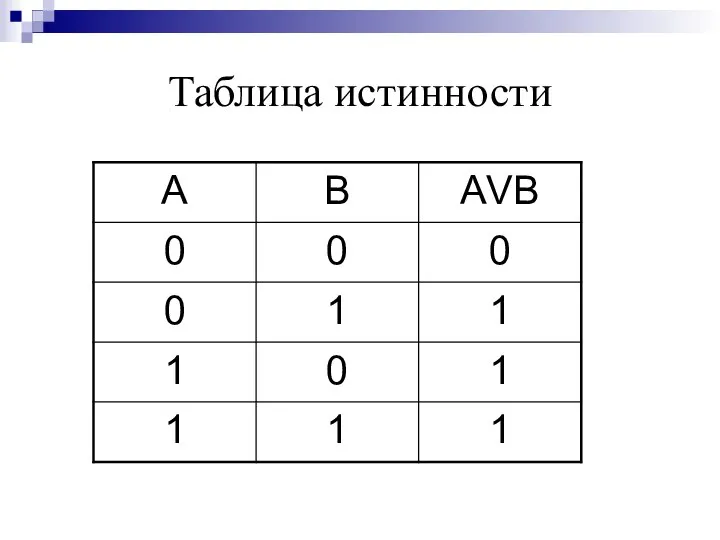
- 16. Логическая операция ДИЗЪЮНКЦИЯ (логическое сложение): в естественном языке соответствует союзу или; обозначение V ; в языках
- 17. В алгебре множеств дизъюнкции соответствует операция объединения множеств, т.е. множеству получившемуся в результате сложения множеств А
- 18. Таблица истинности
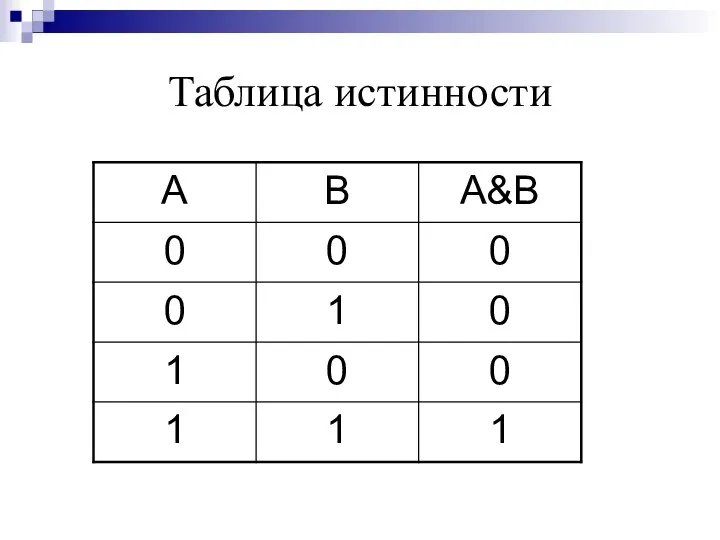
- 19. Логическая операция КОНЪЮНКЦИЯ (логическое умножение): в естественном языке соответствует союзу и; в алгебре высказываний обозначение &;
- 20. В алгебре множеств конъюнкции соответствует операция пересечения множеств, т.е. множеству получившемуся в результате умножения множеств А
- 21. Таблица истинности
- 22. Логическая операция ИНВЕРСИЯ (отрицание):
- 23. В алгебре множеств логическому отрицанию соответствует операция дополнения до универсального множества, т.е. множеству получившемуся в результате
- 24. Таблица истинности:
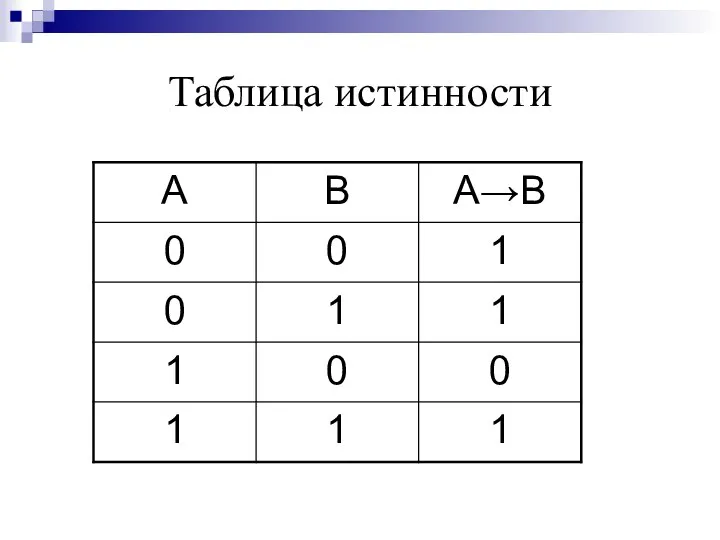
- 25. Логическая операция ИМПЛИКАЦИЯ (логическое следование): в естественном языке соответствует обороту если ..., то ...; обозначение А
- 26. Таблица истинности
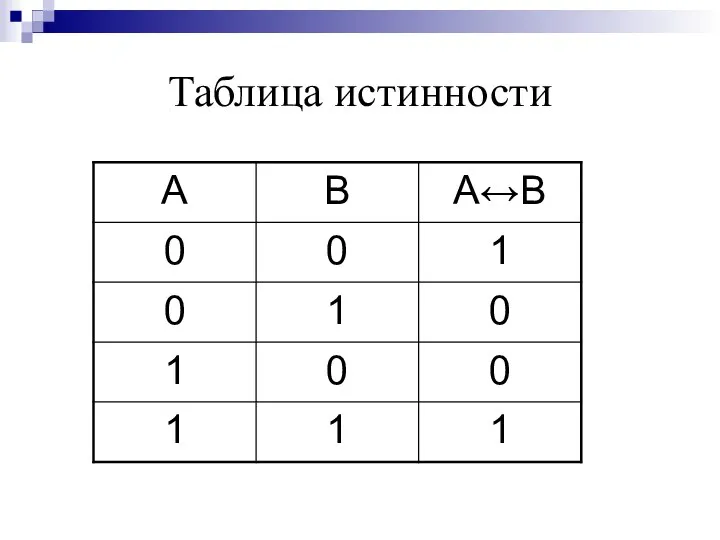
- 27. Логическая операция ЭКВИВАЛЕНЦИЯ (равнозначность): В естественном языке соответствует оборотам речи тогда и только тогда; в том
- 28. Таблица истинности
- 29. Логические операции имеют следующий приоритет: действия в скобках, инверсия, &, V, →, ↔.
- 30. Простые и сложные высказывания
- 31. Задание 1. Определите истинность составного высказывания: ( A & B ) & (C V D), состоящего
- 32. Решение: А = 1, В = 0, С = 1, D = 0. ( 1 &
- 33. Задание 2. Выделите в составных высказываниях простые. Обозначьте каждое их них буквой; запишите с помощью логических
- 34. Задание 3. Найдите значения логических выражений а) (1V1)V(1V 0); б) ((1V0)V1)V1; в) (0V1)V(1V0); г) (0&1)&1; д)
- 35. Задание 4. Даны два простых высказывания (устно): А = {2 * 2 = 4}, В =
- 37. Скачать презентацию

























 Презентация на тему Влияние на организм младшего школьника компьютерных игр
Презентация на тему Влияние на организм младшего школьника компьютерных игр  Информатика. Вводная лекция
Информатика. Вводная лекция Информационные процессы
Информационные процессы Автоматизация предоставления услуг
Автоматизация предоставления услуг Application Stepsfor Students
Application Stepsfor Students Информация для родителей. Безопасный интернет
Информация для родителей. Безопасный интернет Инструкция по удаленному подключению к компьютеру ЗКВС
Инструкция по удаленному подключению к компьютеру ЗКВС Снегопад
Снегопад Кодирование и обработка звуковой информации
Кодирование и обработка звуковой информации Автоматизация напоминалок
Автоматизация напоминалок Операции с целыми числами в языке PASCAL. Операция DIV
Операции с целыми числами в языке PASCAL. Операция DIV Визуализация табличных данных путем создания различных карт
Визуализация табличных данных путем создания различных карт Лекция10
Лекция10 Кредитный конфигуратор. Архитектура
Кредитный конфигуратор. Архитектура Система ввода/вывода языка программирования. Лекция 12
Система ввода/вывода языка программирования. Лекция 12 Mit App Inventor. Компонент текст, переменные, арифметика (урок 2)
Mit App Inventor. Компонент текст, переменные, арифметика (урок 2) 50 главных категорий контента
50 главных категорий контента Встреча с AMD
Встреча с AMD Быть в 10 раз эффективнее благодаря Groovy
Быть в 10 раз эффективнее благодаря Groovy Тест по основам программирования. Pascal
Тест по основам программирования. Pascal Работа с файлами (ввод и вывод)
Работа с файлами (ввод и вывод) Simulink. Компьютерные технологии при разработке и проектировании электрооборудования автономных объектов
Simulink. Компьютерные технологии при разработке и проектировании электрооборудования автономных объектов Поисковые системы. Интернет
Поисковые системы. Интернет Моя жизнь в моём мире
Моя жизнь в моём мире Тема 6. Организация службы защиты информации (СЗИ)
Тема 6. Организация службы защиты информации (СЗИ) Презентация на тему Программная оболочка Norton Commander
Презентация на тему Программная оболочка Norton Commander  Уро13_Адаптивная верстка
Уро13_Адаптивная верстка Типы информационных моделей. Табличные ИМ
Типы информационных моделей. Табличные ИМ