Формат с плавающей точкой (float)

Любое число в экспоненциальной форме имеет множество представлений.
1=0,00001*105=1000*10-3 и т.д.
Среди этих представлений выделили нормализованное представление числа:
2008(10)=0,2008*104
Для каждого числа это представление – единственное.
1=0,1*101
При нормализированном представлении числа в экспоненциальной форме мантисса (М) должна быть в интервале
0,1(d)≤М<1(d), где d – основание системы счисления.

Операнды в цифровом процессоре в формате с плавающей точкой (ПТ) - float представляют числа в экспоненциальной форме.
Такой формат чисел в компьютерах используется в для научно-технических расчетов, когда в вычислениях диапазон чисел может варьироваться от очень малых величин до очень больших, т.е. нужно обеспечить большой диапазон вычислений. Это плюс.
Но в отличие от формата с ФТ, в котором выполняются абсолютно точные вычисления, операции в таком формате выполняются с приближением, определяемым разрядной сеткой процессора.

В истории IT- технологий существовало много форматов чисел в формате с ПТ.
В настоящее время общепринятым стандартом представления операндов в формате с плавающей точкой в цифровом процессоре является стандарт IEEE 754.
В IEEE 754:
мантисса представляется в прямом коде;
порядок «смещен» (увеличен) на константу.

Смещение порядка на константу позволяет обойтись без явного бита знака порядка. Если значение смещенного порядка больше константы смещения, он – положительный, если меньше – отрицательный. Такое решение позволило реализовать более простые алгоритмы операций над порядками.
Если константа смещения равна 127, то:
0,1*10-3 будет записано, как 0,1*10-124;
0,2008*104 будет записано, как 0,2008*10131

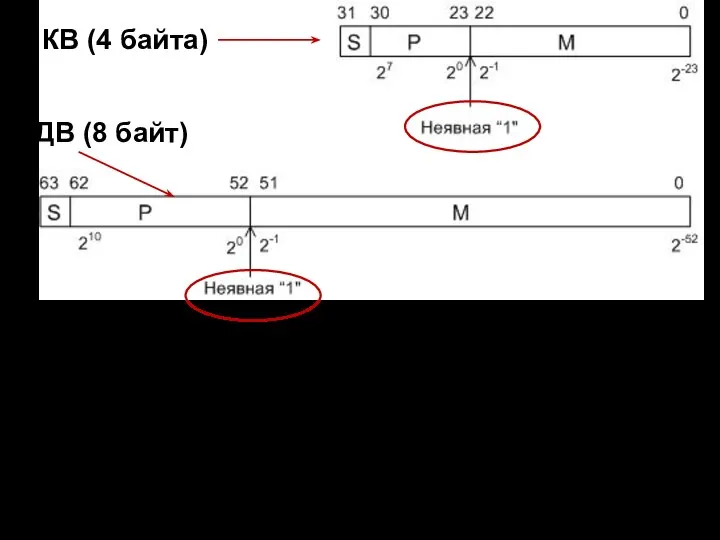
Есть два формата представления чисел с плавающей точкой стандарта IEEE 754 в оперативной памяти процессора :
«короткое вещественное (КВ)»,
«длинное вещественное (ДВ)».
Они отличаются диапазоном представимых в них чисел.
В самом процессоре арифметические операции выполняются всегда в формате:
«внутреннее (расширенное) вещественное (ВВ)».
Т.е. при передаче из оперативной памяти в процессор форматы КВ и ДВ преобразуются в ВВ и наоборот.

Используются следующие обозначения: М – мантисса числа; S – знак мантиссы; Р – порядок числа.
В формате КВ под мантиссу отводится 24 бит, а под порядок – 8 бит. Величина порядка операнда смещена на 127(10), т.е. Р=Рх+127(10).
В формате ДВ под мантиссу отводится 53 бит, а под порядок –
11 бит. Величина порядка операнда смещена на 1023(10), т.е. Р=Рх+1023(10).
КВ (4 байта)
ДВ (8 байт)

«Скрытый» бит мантиссы
Поскольку при нормализованном представлении операнда (0,1(2)≤ М<1(2)) в двоичной системе счисления первая цифра мантиссы после запятой всегда будет равна «1», т.е. 0,1…………
это можно использовать для увеличения диапазона представимых чисел в оперативной памяти, для чего диапазон представления мантиссы нормализованного числа в стандарте IEEE 754 меняется на диапазон
1(2)≤М<2(2).
Причем единица целой части мантиссы учитывается неявно (неявная единица), т.е. под нее не отводится бит. В таком виде операнд хранится в памяти процессора. При выполнении арифметических операций над операндом, при его извлечении из памяти в регистр процессора (формат ВВ) этот скрытый бит восстанавливается, т.е. присутствует в явном виде

Алгоритм преобразования вещественного десятичного числа в двоичное число с плавающей точкой формата IEEE 754
( на примере числа = 8,125(10))
1.Перевести целую часть вещественного числа в двоичную систему и поставить после нее десятичную точку (для заданного примера: 1000).
2. Перевести дробную часть вещественного числа в двоичную систему с точностью для определения значений всех битов мантиссы, предусмотренных форматом (КВ, ДВ, ВВ) (для заданного примера: 0,0010…0)

3. Записать полученное значение дробной части после десятичной точки. Если значение
мантиссы меньше выделенного под нее количества разрядов, то дополнить дробную часть незначащими
нулями справа до предусмотренного форматом размера. Для заданного примера:
1000,001000000000000000000000000 (всего 31 бит)
4. Представить число в экспоненциальной форме. Для заданного примера:
0, 1000001000000000000000000000000*10100

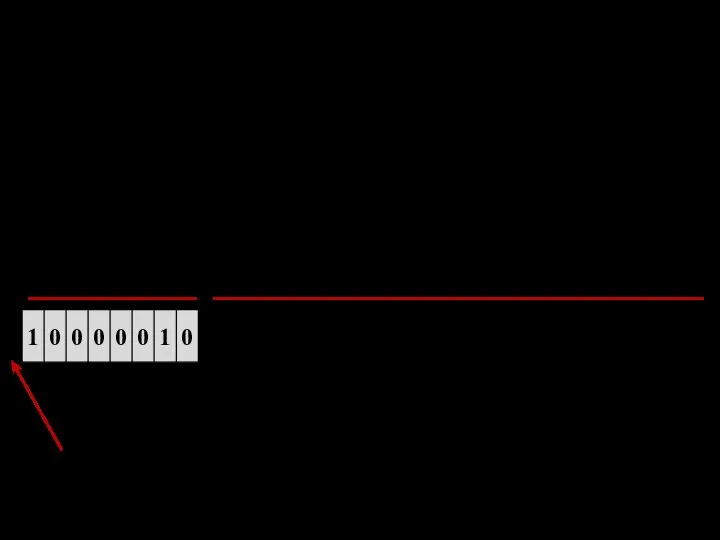
5. Нормализовать полученное двоичное
число (1(2)≤М<2(2)), определив тем самым значение порядка. Для заданного примера:
1,0000010000000000000000000000000*1011
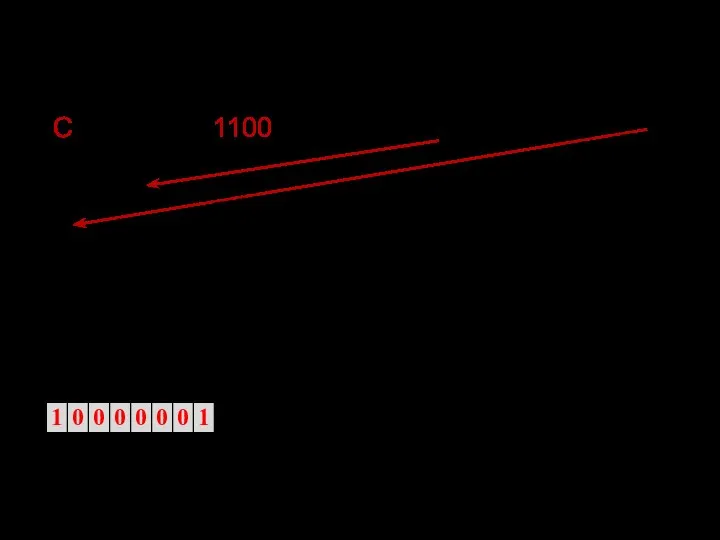
6. К порядку прибавить смещение в соответствии с форматом, и представить его в двоичном виде. В результате будет получен смещенный порядок для выбранного формата (для заданного примера: 3+127=130=10000010(2)).

7. Записать значение порядка и значение мантиссы в соответствующие биты формата КВ или ДВ (у мантиссы, отбрасывается единица целой части).
8. Если число положительное, то в самый старший разряд (знак мантиссы) следует записать 0, если отрицательное, то 1.
мантисса
порядок
знак мантиссы

Рассмотрим другие примеры представления операндов в формате КВ.
Напоминание:
мантисса – М (1(2)≤М<2(2));
порядок – Р (смещен на 127(10)).
Пример. Представить число 16,АС(16) в формате КВ.
Перевод в двоичную систему:
16,АС(16)=10110,10101100(2)=1,011010101100(2)*10100.
М=1,011010101100(2);
Р=100(2)+(127(10)=1111111(2))=10000011(2).
Тогда формат КВ этого числа (красным цветом выделены биты порядка) будет (целая часть мантиссы «скрыта»):

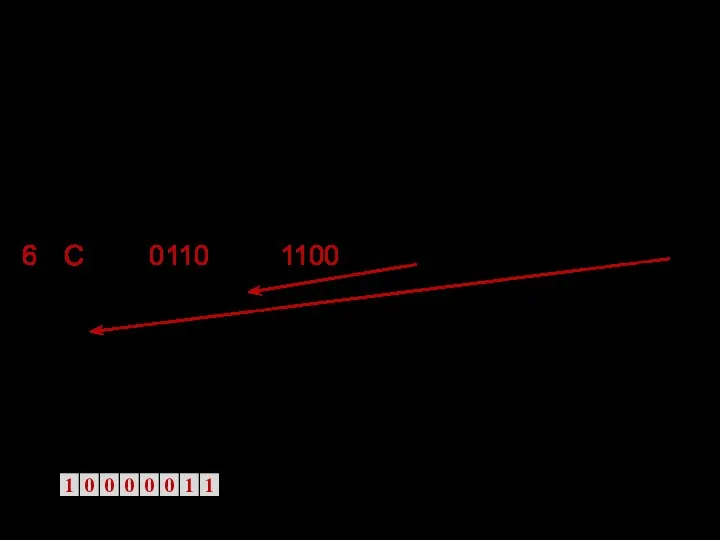
Еще пример:
Представить число – 7,С8(16) в формате КВ.
Перевод:
–7,С8(16)= –111,11001000(2)= –1,1111001000(2)*1010.
М= – 1,1111001000(2);
Р=10(2)+(127(10)=1111111(2))=10000001(2).
Тогда формат КВ этого числа (красным цветом выделены биты порядка) будет(целая часть мантиссы «скрыта»):