Содержание
- 2. В практике машинного моделирования сложных систем используется вычислительная техника трех типов: ЭВМ(электронная вычислительная машина), АВМ (аналоговая
- 3. Рассмотрим достоинства и недостатки этих трех типов вычислительных средств (АВМ, ЭВМ и ГВК) применительно к машинному
- 4. 5) операции сложения, вычитания, умножения, дифференцирования, интегрирования, генерирования непрерывных функций выполняются весьма эффективно, но имеются ограниченные
- 5. Характерные черты ЭВМ: 1) вся обработка промежуточной и результирующей информации в процессе моделирования системы S реализуется
- 6. 6) применяется ограниченное число арифметических операций(сложение, вычитание, умножение и деление), но с помощью численных методов можно
- 7. При этом цифровая часть ГВК дает возможность: 1) управлять аналоговой частью машинной модели Мм при высоком
- 8. Преимущества ГВК: 1) сочетает быстродействие АВМ и точность ЭВМ, что позволяет расширить класс моделируемых объектов; 2)
- 9. Говорить о преимуществах и недостатках ГВК можно применительно к машинному моделированию конкретного класса систем S. Для
- 10. Для сложных динамических объектов перспективным является моделирование на базе ГВК, которые реализуют преимущества цифрового и аналогового
- 11. Состав и структура технического обеспечения АЦМК определяется множеством задач, на решение которых он ориентирован. В общем
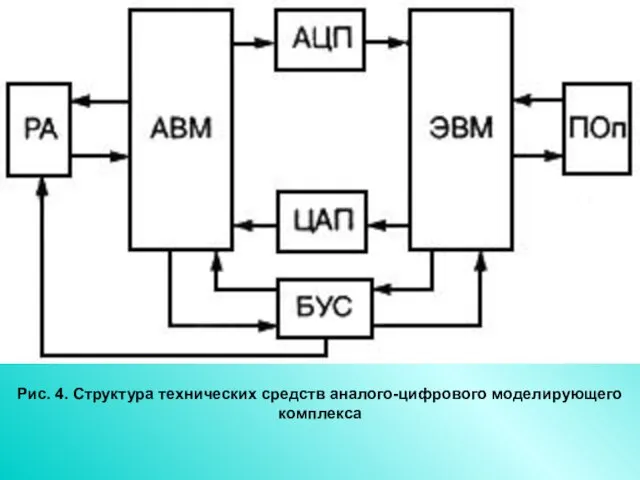
- 12. Рис. 4. Структура технических средств аналого-цифрового моделирующего комплекса
- 13. Преобразователи АЦП и ЦАП являются средствами организации информационных связей между АВМ и ЭВМ, т. е. средствами
- 14. Оператор управляет процессом моделирования с помощью средств, номенклатура которых определяется задачами, решаемыми на АЦМК. В состав
- 15. Аналого-ориентированные комплексы используются в тех случаях, когда не требуется высокая точность результатов и когда моделируемая система
- 16. К цифро-ориентированным комплексам можно отнести универсальные ЭВМ, где для отображения и регистрации результатов используются аналоговые средства
- 17. Сбалансированные (универсальные) комплексы являются самым мощным средством для решения задач аналого-цифрового моделирования. В их состав входят
- 18. Задача построения технического обеспечения АЦМК в настоящее время сводится к выбору стандартной аппаратуры, разработке информационных и
- 19. Современные АВМ, как правило, позволяют осуществлять цифровое управление. Принципиальных трудностей в построении технического обеспечения АЦМК нет.
- 20. Следует ответить на вопросы: требуется ли работа в реальном масштабе времени, какие устройства должны быть включены
- 21. Прежде всего нужно обосновать преимущества гибридного моделирования системы перед аналоговым или цифровым. При этом задачи, для
- 22. Сложность перечисленных вопросов заключается в том, что большинство из них взаимосвязаны. От правильности их решения зависит
- 23. Логическая компоновка подразумевает выбор минимального состава устройств, агрегатов и модулей из номенклатуры определенных семейств вычислительной техники,
- 24. Опишем вариант построения АЦМК для решения задачи моделирования системы S на базе управляющей ЭВМ, которая имеет
- 25. Рассмотрим особенности компоновки устройств организации информационных и управляющих связей между ЭВМ и АВМ. Вариант использования ЭВМ
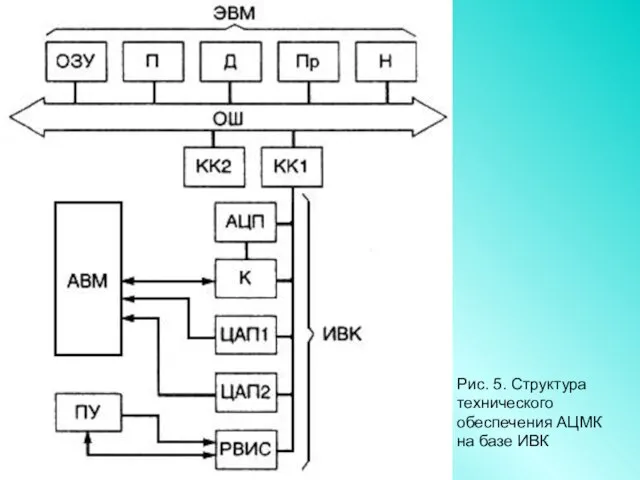
- 26. Пример 1. Рассмотрим возможности построения технического обеспечения АЦМК на базе ИВК (рис. 5.5). В данной структуре
- 27. Рис. 5. Структура технического обеспечения АЦМК на базе ИВК
- 28. Развитая операционная система современных ЭВМ позволяет реализовать на их основе процедуры генерации цифровой части модели Мм,
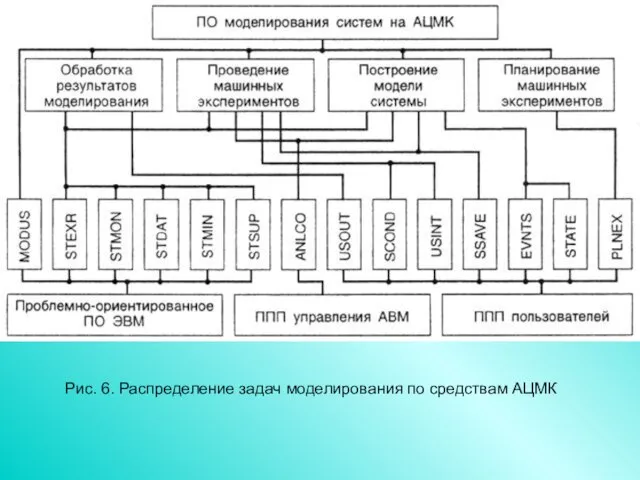
- 29. Программное обеспечение (ПО) АЦМК (рис. 6) строится по модульному принципу и включает в себя комплексы программ:
- 30. Рис. 6. Распределение задач моделирования по средствам АЦМК
- 31. Пример 2. Рассмотрим состав ПО АЦМК. В зависимости от вида модели конкретной системы S ППП пользователя
- 32. Решая задачу моделирования конкретной системы S, пользователь может отказаться от использования тех или иных программ. MONIT
- 33. Наиболее сложная часть ПО - комплекс программных средств ЭВМ. Не останавливаясь на рассмотрении операционной системы MODOS,
- 34. Использование модульной структуры и организации ПО моделирования позволяет в режиме генерации создавать ППМ конкретной системы S,
- 35. Тема КОМПЬЮТЕРНОЕ МОДЕЛИРОВАНИЕ НА МИКРОУРОВНЕ
- 36. Объекты компьютерного моделирования на микроуровне
- 37. Микроуровень – это нижний иерархический уровень декомпозиции объектов проектирования по степени абстрагирования при составлении математического описания.
- 38. Общий вид уравнений математической модели описания физических свойств технического объекта с распределенными параметрами (1) или ,
- 39. Если уравнение содержит одну фазовую переменную, система описывается одним уравнением вида (1), если несколько фазовых переменных,
- 40. Уравнение (1) имеет множество решений. Для получения единственного решения необходимо задать краевые условия, включающие граничные и
- 41. Существует несколько стандартных способов задания граничных условий. Для теплового объекта, представляющего собой твердое гомогенное (однородное) тело,
- 42. Объекты с распределенными параметрами могут быть различной физической природы: электрические, механические, тепловые, гидравлические, магнитные и др.
- 43. При анализе гидравлических и пневматических систем определяют режимы течения сплошных потоков жидкостей и газов, характеризуемые скоростями
- 44. Основы построения компьютерных моделей элементов систем на микроуровне
- 45. Для построения компьютерных моделей технических объектов с распределенными параметрами используют фундаментальные физические законы. К ним относятся
- 46. У трехмерного технического объекта вектор состоит из трех составляющих, направленных параллельно осям декартовой системы координат х,
- 47. Уравнение закона сохранения массы , (4) где ρ – плотность массы, кг/м3; (5) – вектор плотности
- 48. Уравнение закона сохранения энергии (7) где – полная энергия единицы массы (е – внутренняя энергия единицы
- 49. Уравнение закона сохранения количества движения используют при моделировании движения потока жидкости. Для потока идеальной жидкости (без
- 50. Для одномерного потока жидкости получаем . (10) При учете массовых сил и сил трения уравнение закона
- 51. Модели механических подсистем на микроуровне
- 52. Надежность работы ПрМ определяется рациональным выбором геометрических параметров входящих в их состав механических элементов. Форма и
- 53. Современные методы анализа напряженно-деформированного состояния несущих элементов различных технических систем базируются на использовании моделей с распределенными
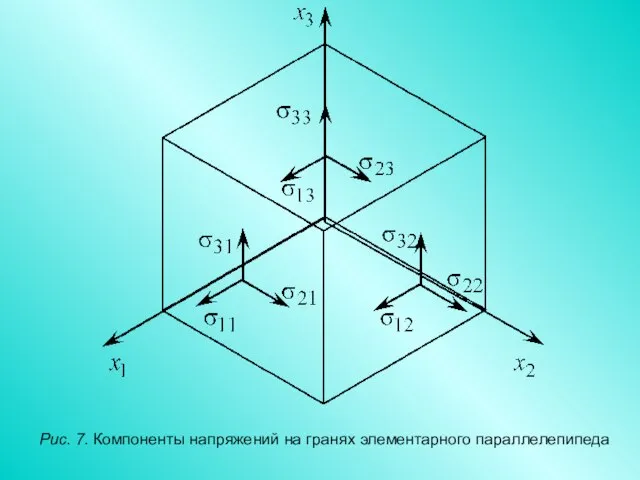
- 54. Рис. 7. Компоненты напряжений на гранях элементарного параллелепипеда
- 55. Выделим в твердом теле элементарный параллелепипед (рис. 7). Сформулируем условия его равновесия: геометрическая сумма сил, приложенных
- 56. В случае линейной зависимости между ними, устанавливаемой законом Гука, для анизотропного тела имеем (13) при i
- 57. Заменив напряжения на деформации в уравнениях равновесия (12), получим уравнение теории упругости, называемое уравнением Ламе: (18)
- 58. Поэтому модель представляют в виде выражения потенциальной энергии Еп системы как разность энергии деформации Ед и
- 59. Используя матрицу (19), уравнения (13) и (14) можно записать в лаконичной форме (20) При использовании принципа
- 60. Модели тепловых систем на микроуровне
- 61. Теплообмен может осуществляться теплопроводностью, конвекцией и тепловым излучением. Температурным полем называется совокупность значений температуры для всех
- 62. Уравнение теплопроводности может быть получено на основе закона сохранения энергии. Применительно к тепловой системе закон сохранения
- 63. Выделение (или поглощение) тепловой энергии внутри тела может происходить из-за объемных химических реакций, прохождения электрического тока,
- 64. С учетом выражений (39) и (40) уравнение (38) приводится к виду . (41) Для однородного изотропного
- 65. Для одномерного случая, когда теплопередача осуществляется только вдоль оси х, получаем . (44) Для решения уравнений
- 66. Для многих теплотехнических объектов можно принимать GQ = 0. К ним, в частности, относятся объекты, представляющие
- 67. При описании граничных условий в зависимости от наличия информации о теплообмене на граничной поверхности принимают различные
- 68. Учитывая формулу (40), можно отметить, что граничные условия второго рода характеризуют распределение плотности теплового потока на
- 69. Граничные условия третьего рода позволяют конкретизировать характеристики теплообмена с внешней средой. При этом задается распределение плотности
- 70. Уравнение (50) выражает закон Ньютона. Принимая во внимание, что, согласно выражению (40), модуль вектора плотности теплового
- 71. Если положить α → 0, получим частный случай граничных условий второго рода – при теплоизолированной граничной
- 72. На основе выражений (47)–(53) можно получить уравнения граничных условий для одномерного теплотехнического объекта. Уравнения граничных условий
- 73. Если какая-либо из границ (правая или левая) теплоизолирована, то для этой границы. Граничные условия третьего рода
- 74. при теплообмене излучением (58) где и – температура окружающей среды, соответственно, на левой и правой границах;
- 75. При анализе температурных полей все части объекта необходимо рассматривать совместно. Для каждой части (слоя) записывают свое
- 76. При этом задается распределение температуры по всей области определения объекта Ω в начальный момент времени при
- 77. Пример разработки модели
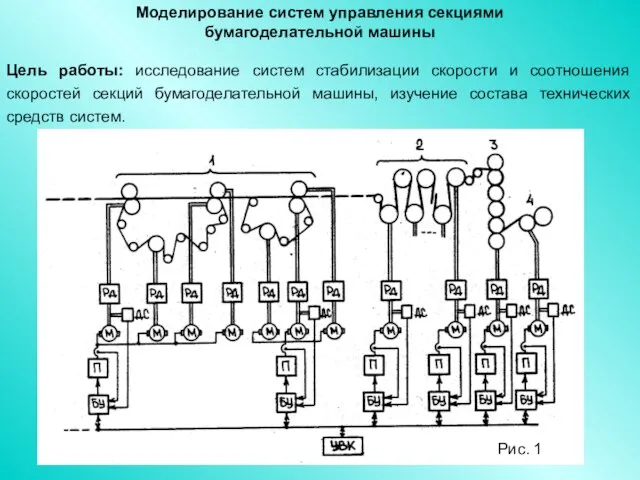
- 78. Моделирование систем управления секциями бумагоделательной машины Цель работы: исследование систем стабилизации скорости и соотношения скоростей секций
- 79. Описание объекта моделирования (Рис. 1 ). Бумажное полотно формируется из бумажной массы в результате нескольких непрерывно
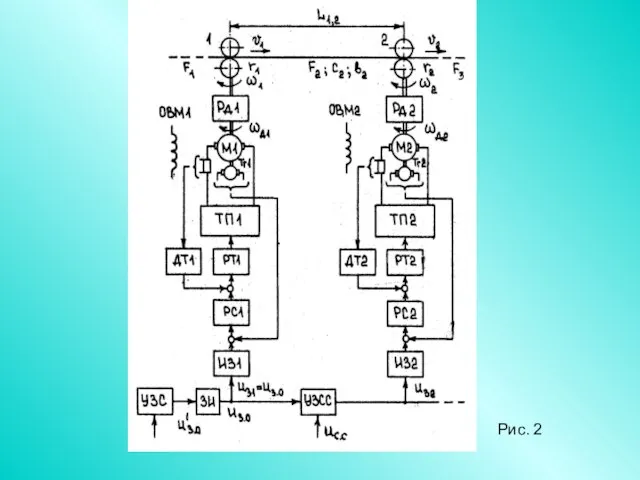
- 80. Рис. 2
- 81. Функциональная схема системы управления двумя смежными секциями показана на рис. 2. Механизмы секций машины представлены в
- 82. Таблица 1
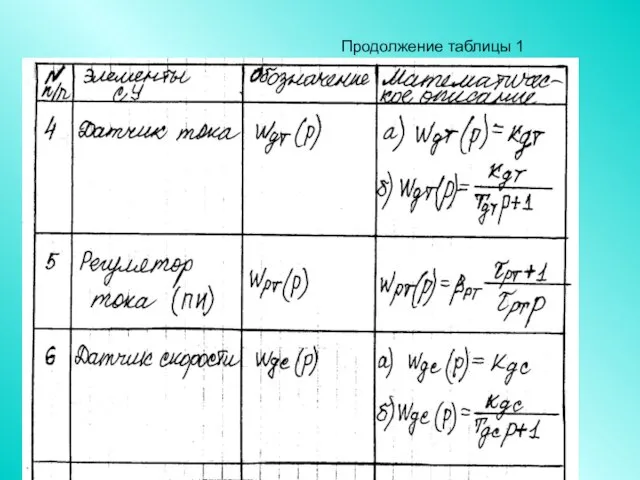
- 83. Продолжение таблицы 1
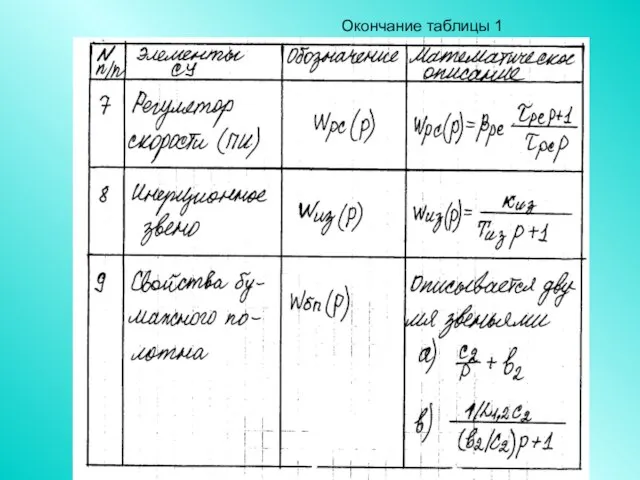
- 84. Окончание таблицы 1
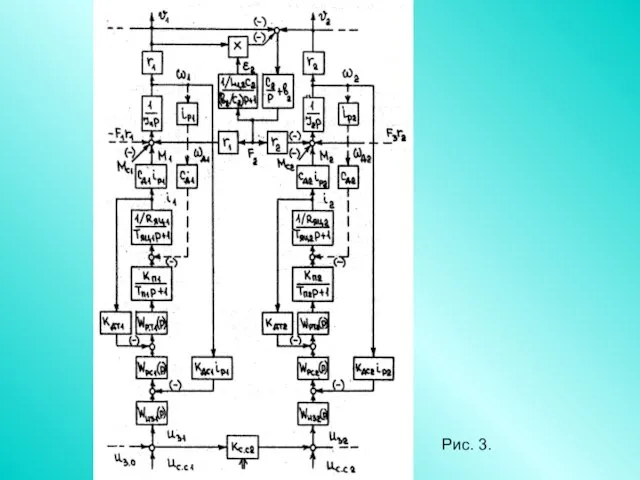
- 85. Рис. 3.
- 86. Исходными данными к выполнению работы являются данные секций и режим работы машины, состав технических средств (комплектных
- 90. Скачать презентацию














































































 ПО робоавтомобиля: алгоритмы распознавания и управления
ПО робоавтомобиля: алгоритмы распознавания и управления Информационные системы в бизнес проектировании
Информационные системы в бизнес проектировании Маршрутизация. Контроллеры. Представления. Хелперы
Маршрутизация. Контроллеры. Представления. Хелперы Управление деятельностью и координация работы телеканалов
Управление деятельностью и координация работы телеканалов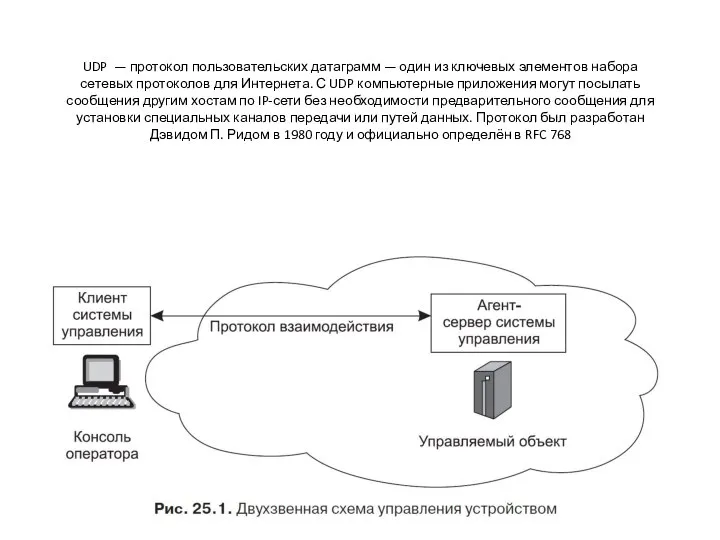 UDP — протокол пользовательских датаграмм
UDP — протокол пользовательских датаграмм Электронные таблицы: общие сведения
Электронные таблицы: общие сведения Инструменты графического редактора Paint
Инструменты графического редактора Paint Создание Telegram бота для решения квадратных уравнений
Создание Telegram бота для решения квадратных уравнений Презентация на тему Действия с информацией (4 класс)
Презентация на тему Действия с информацией (4 класс)  Исправление ошибок в простой программе с условными операторами. ЕГЭ 24
Исправление ошибок в простой программе с условными операторами. ЕГЭ 24 Test. Thunkable
Test. Thunkable IT-технологии. Роботехника в Политехе
IT-технологии. Роботехника в Политехе Индивидуальная домашняя самостоятельная работа
Индивидуальная домашняя самостоятельная работа Табличный процессор Excel
Табличный процессор Excel Правила ввода и решения задач с одномерными массивами. Часть 1
Правила ввода и решения задач с одномерными массивами. Часть 1 Гиперпространство
Гиперпространство Результаты поиска литературы в электронных каталогах библиотек
Результаты поиска литературы в электронных каталогах библиотек Ma‘lumotlar bazasini boshqarish tizimlari
Ma‘lumotlar bazasini boshqarish tizimlari 3D моделирование. Викторина
3D моделирование. Викторина Панель рисования в MS Word
Панель рисования в MS Word Смайлики в електроних листах
Смайлики в електроних листах lesson11
lesson11 Внешние устройства ПК
Внешние устройства ПК Разработка информационной многопользовательской клиент-серверной системы по навигационным измерительным устройствам
Разработка информационной многопользовательской клиент-серверной системы по навигационным измерительным устройствам Комментарии в стиле С++
Комментарии в стиле С++ Магнитная память
Магнитная память _Р221+Тестировщик+ПО (1)
_Р221+Тестировщик+ПО (1) Установка кистей
Установка кистей