Содержание
- 2. Источники Аляев Ю. А., Тюрин С. Ф. Дискретная математика и математическая логика. Андерсон Дж. Дискретная математика
- 3. Задание графа
- 4. Граф
- 5. Орграф
- 6. Задание графа
- 7. Задание графа
- 8. Задание графа
- 9. Задание орграфа
- 10. Матрица инцидентности орграфа
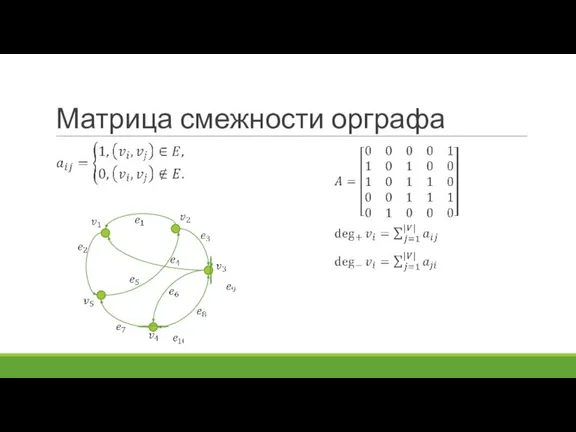
- 11. Матрица смежности орграфа
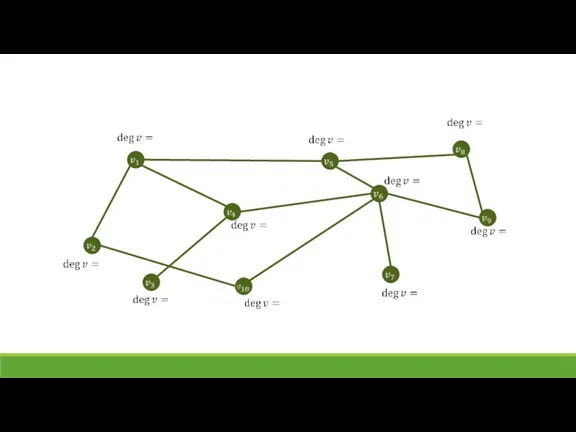
- 12. Степень (валентность) вершины
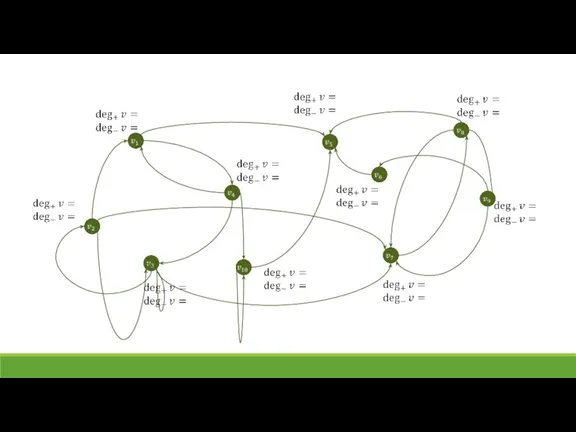
- 13. Полустепень
- 16. Теорема
- 17. Теорема
- 18. Особые графы
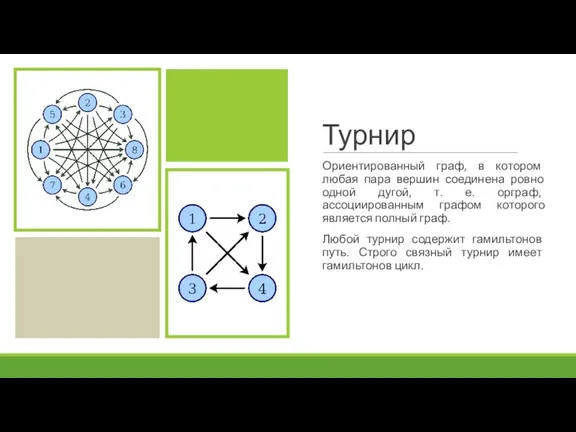
- 19. Турнир Ориентированный граф, в котором любая пара вершин соединена ровно одной дугой, т. е. орграф, ассоциированным
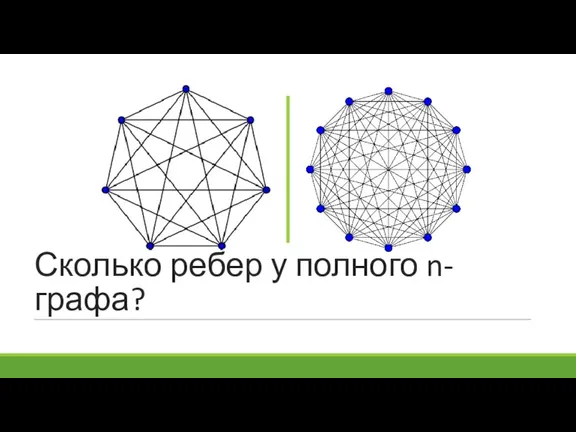
- 20. Сколько ребер у полного n-графа?
- 21. Сколько ребер у полного n-графа?
- 22. Мультиграфы и псевдографы
- 23. Петли
- 24. Кратные рёбра Если в графе существуют несколько рёбер, соединяющих одну и ту же вершину, то такие
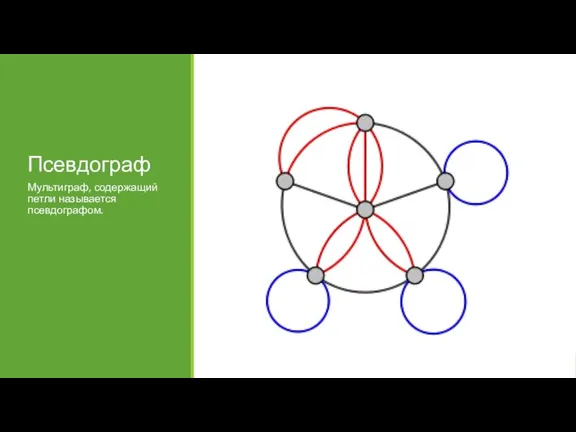
- 25. Псевдограф Мультиграф, содержащий петли называется псевдографом.
- 26. Двудольный граф
- 27. Двудольные графы
- 28. Полным двудольным графом называется специальный вид двудольного графа, у которого любая вершина первой доли соединена со
- 29. Маршруты и пути
- 30. Маршрут
- 31. Маршрут
- 32. Цепь
- 33. Цикл
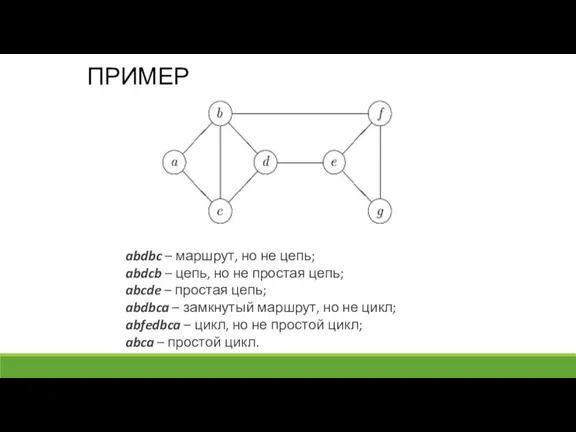
- 34. ПРИМЕР abdbc – маршрут, но не цепь; abdcb – цепь, но не простая цепь; abcde –
- 35. Определить 2,3,4,5,1,2- цикл? 2,3,5,4 – маршрут? НЕТ 2,3,4,5,1,4,3- маршрут? ДА а цепь? НЕТ 3,1,4,5,1,2- цепь? ДА
- 36. Каждая внутренняя вершина незамкнутой цепи инцидентна не менее, чем рёбрам, концевые вершины инцидентны минимум одному ребру.
- 37. Свойства
- 38. Лемма. Всякий маршрут графа содержит хотя бы одну простую цепь, соединяющую ту же пару вершин. Доказательство
- 39. Путь
- 40. Свойства орграфа В каждом бесконтурном графе имеется хотя бы одна вершина, полустепень исхода которой равна нулю.
- 41. Связность
- 42. Связность графа Две различные вершины графа называются связными, если существует соединяющая их простая цепь. В противном
- 43. Пример
- 44. Связность орграфа
- 45. Матрицы связности и достижимости
- 46. Матрицы связности и достижимости
- 47. Эйлеров граф
- 48. Задача о семи кёнигсбергских мостах Издавна среди жителей Кёнигсберга была распространена такая загадка: как пройти по
- 49. Решение задачи по Эйлеру На упрощённой схеме части города (графе) мостам соответствуют линии (дуги графа), а
- 50. Эйлеров цикл и Эйлерова цепь Цикл называется эйлеровым, если он содержит все ребра графа. Граф называется
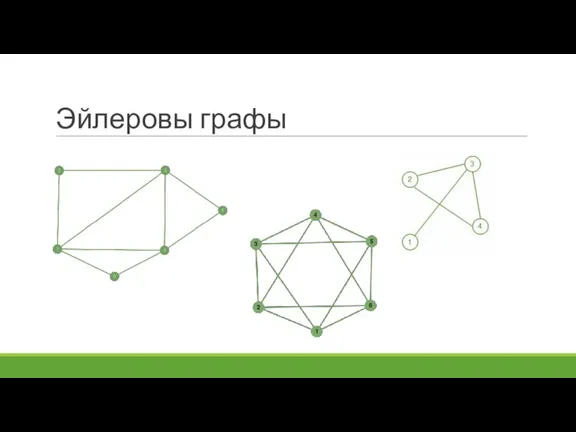
- 51. Эйлеровы графы
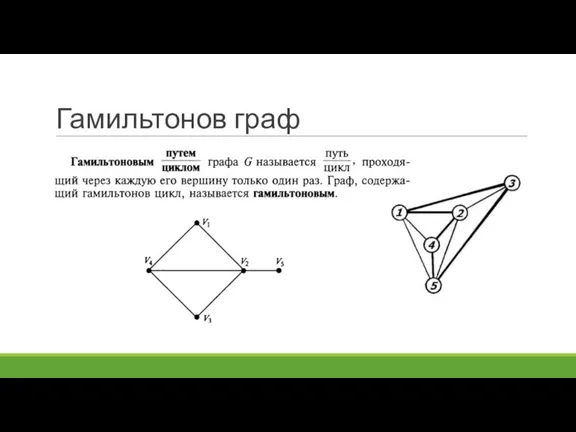
- 52. Гамильтонов граф
- 53. Гамильтонов граф
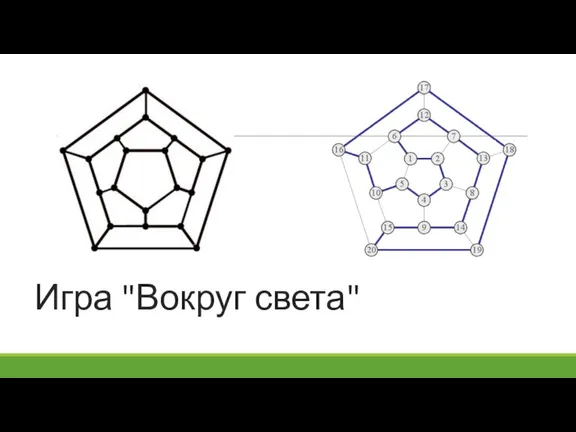
- 54. Игра "Вокруг света"
- 55. Критерий существования гамильтонова цикла в произвольном графе еще не найден. Факты о существовании гамильтоновых циклов в
- 56. Деревья
- 57. Определения Дерево - связный, неориентированный граф без циклов. Лес – граф, компоненты которого являются деревьями.
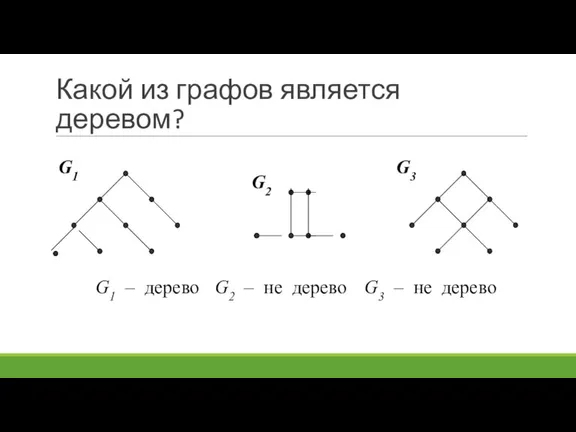
- 58. G1 – дерево G2 – не дерево G3 – не дерево Какой из графов является деревом?
- 59. Листья
- 60. Свойства деревьев
- 61. Свойства деревьев
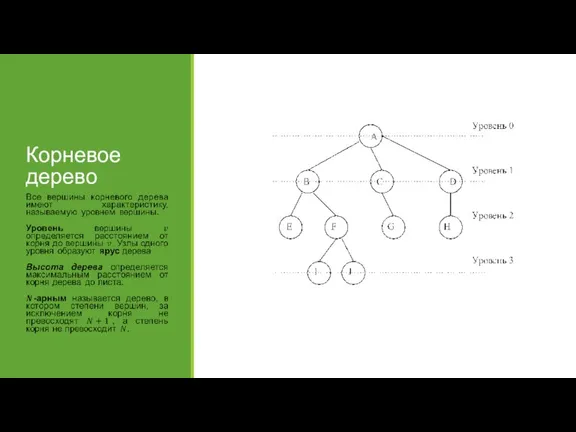
- 62. Корень дерева Пусть дерево представляет физический объект, подвижный в вершинах. Если подвесить дерево за одну из
- 63. Корневое дерево
- 64. Предки и потомки
- 65. Основные соотношения
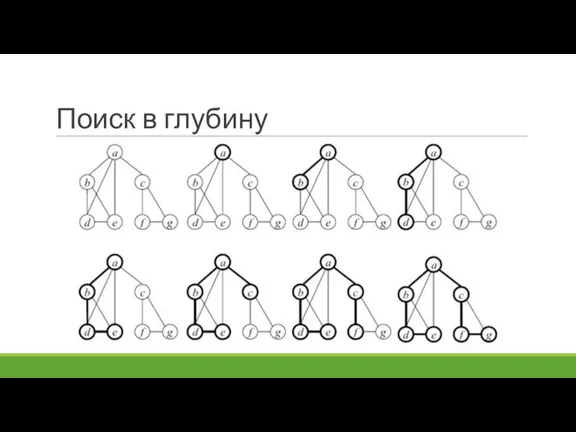
- 66. Поиск в глубину
- 67. Поиск в глубину (англ. depth-first search, DFS)
- 68. Поиск в глубину
- 69. Алгоритм поиска в глубину
- 70. Поиск маршрута в графе; Поиск простого цикла; Выделение компонент связности; Проверка на двудольность; Проверка, является ли
- 71. Поиск в ширину
- 72. Поиск в ширину (англ. breadth-first search, BFS)
- 73. Поиск в ширину
- 74. Применения алгоритма поиска в ширину Выделение компонент связности (подсчёт компонент); Поиск кратчайшего пути в невзвешенном графе;
- 75. Числовые характеристики графа
- 76. Расстояние между вершинами
- 77. Эксцентриситет
- 78. Диаметр графа
- 79. Радиус графа
- 80. Центр графа
- 81. Пример
- 82. Найти диаметр, радиус и центры графа
- 83. Задачи
- 84. Перечислить вершины и рёбра графа.
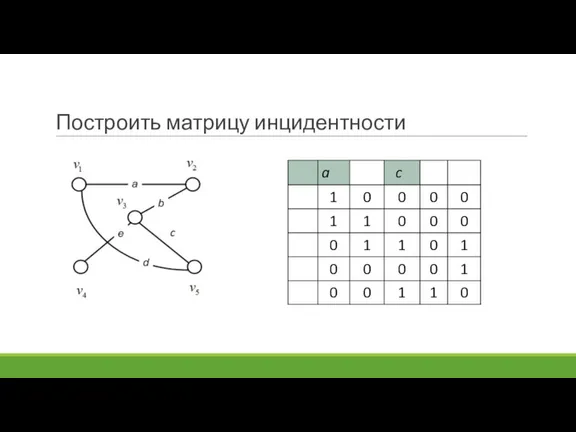
- 85. Построить матрицу инцидентности
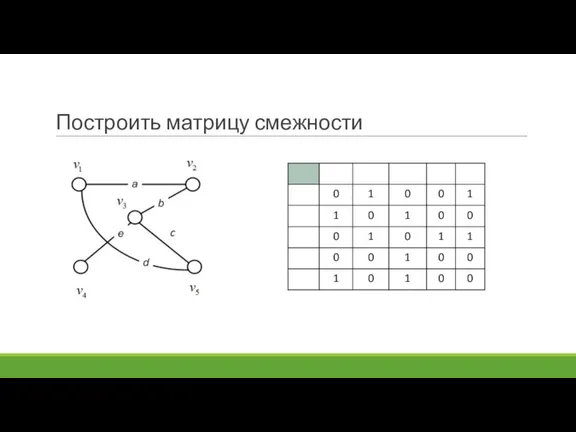
- 86. Построить матрицу смежности
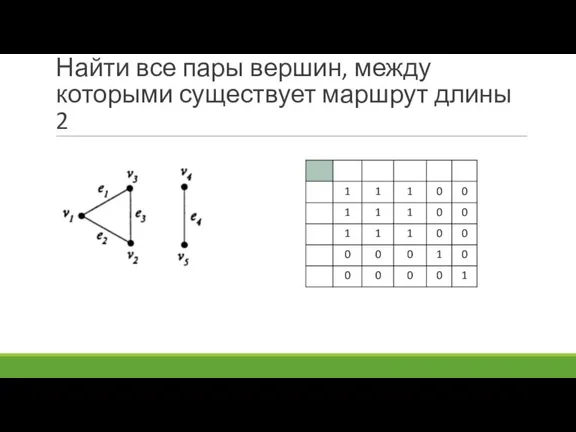
- 87. Найти все пары вершин, между которыми существует маршрут длины 2
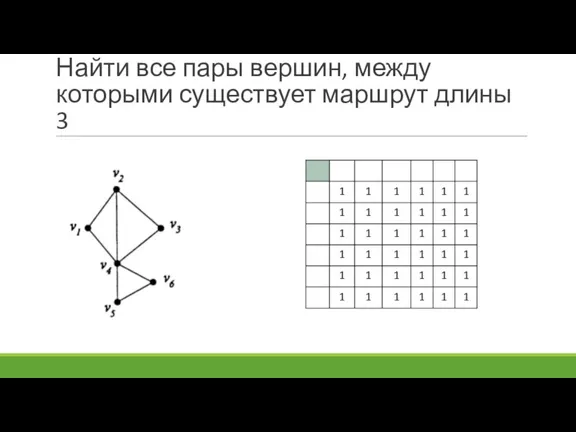
- 88. Найти все пары вершин, между которыми существует маршрут длины 3
- 89. Найти все пары вершин, между которыми существует маршрут длины не меньше 3
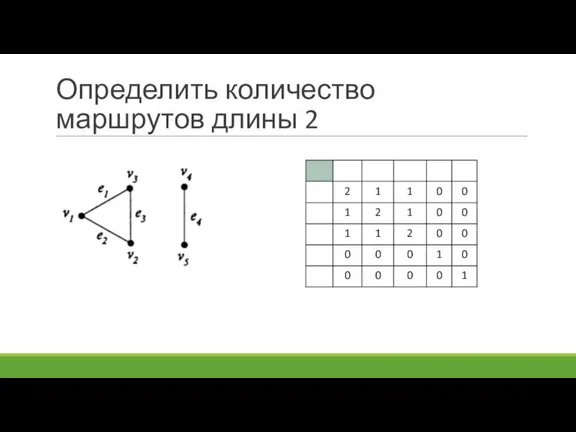
- 90. Определить количество маршрутов длины 2
- 92. Скачать презентацию






































































 Монтаж видео. Переходы
Монтаж видео. Переходы Информационная безопасность организации
Информационная безопасность организации Презентация на тему Решение заданий С3 по информатике
Презентация на тему Решение заданий С3 по информатике  Формы записи, виды алгоритмов
Формы записи, виды алгоритмов Язык программирования Паскаль
Язык программирования Паскаль Базы данных. Запрос параметров
Базы данных. Запрос параметров Brief 1 – Instagram Highlight Covers
Brief 1 – Instagram Highlight Covers Тип данных Массив. Основы программирования
Тип данных Массив. Основы программирования Графический редактор Paint
Графический редактор Paint Персональный компьютер. Компьютер как унивесальное устройство для работы с информацией
Персональный компьютер. Компьютер как унивесальное устройство для работы с информацией Нейронные сети
Нейронные сети Наследование классов. Пример лабораторной 2
Наследование классов. Пример лабораторной 2 Что такое мультимедиа
Что такое мультимедиа Алгоритмическая конструкция ветвление основные алгоритмические конструкции
Алгоритмическая конструкция ветвление основные алгоритмические конструкции Создание векторного рисунка в Microsoft Word
Создание векторного рисунка в Microsoft Word Презентация на тему Виды памяти, вытесняющие статическую память
Презентация на тему Виды памяти, вытесняющие статическую память  Сроки проведения конкурса Страна читалия-2016 и конференции по итогам работы инновационной площадки
Сроки проведения конкурса Страна читалия-2016 и конференции по итогам работы инновационной площадки 03-04. Презентация ДП (1)
03-04. Презентация ДП (1) Информационные технологии и системы. Автоматизированные информационные системы (АИС)
Информационные технологии и системы. Автоматизированные информационные системы (АИС) Презентация на тему Хранение информации
Презентация на тему Хранение информации  Сказ о доблестном Смайл-царевиче и Интернет-страшилищах Поганых
Сказ о доблестном Смайл-царевиче и Интернет-страшилищах Поганых Типы алгоритмов и формы их записи
Типы алгоритмов и формы их записи Проект Spark Drawing
Проект Spark Drawing Безопасное поведение в общественных местах и в сети Интернет
Безопасное поведение в общественных местах и в сети Интернет Введение в этичный хакинг
Введение в этичный хакинг Функции электронных таблиц Microsoft Excel
Функции электронных таблиц Microsoft Excel BIOS. Co to je?
BIOS. Co to je? Создание коллажей. Работа со слоями на изображениях. Урок 20
Создание коллажей. Работа со слоями на изображениях. Урок 20