Graph theory, definitions and examples. Lecture 8,

Definitions and examples

Definitions and examples
Euler (1707 – 1783) was born in Switzerland and spent most of his long life in Russia (St Petersburg) and Prussia (Berlin).
He was the most prolific mathematician of all time, his collected works filling more than 70 volumes.

Definitions and examples
Like many of the very great mathematicians of his era, Euler contributed to almost every branch of pure and applied mathematics.
He is also responsible, more than any other person, for much of the mathematical notation in use today.

Definitions and examples
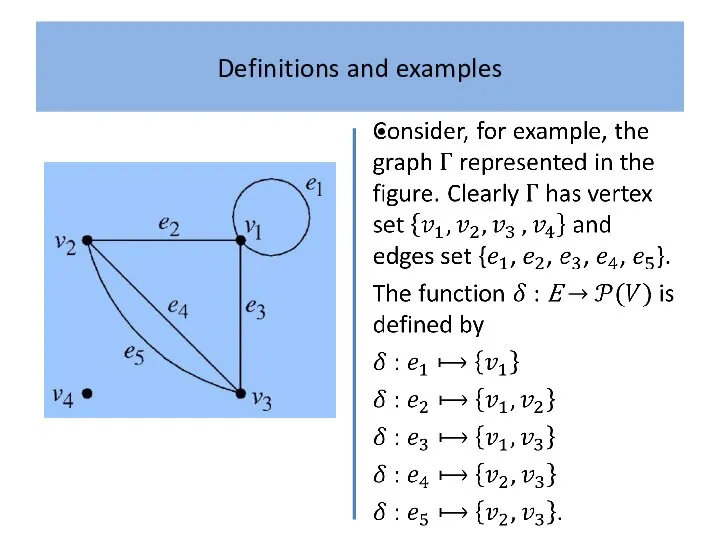
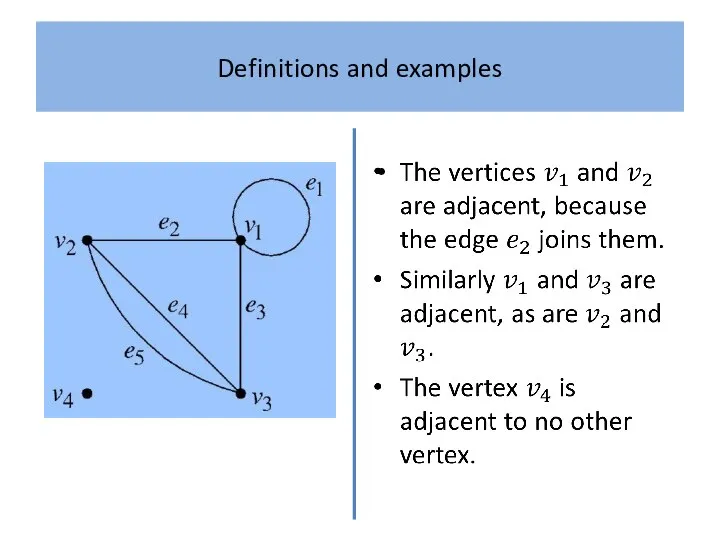
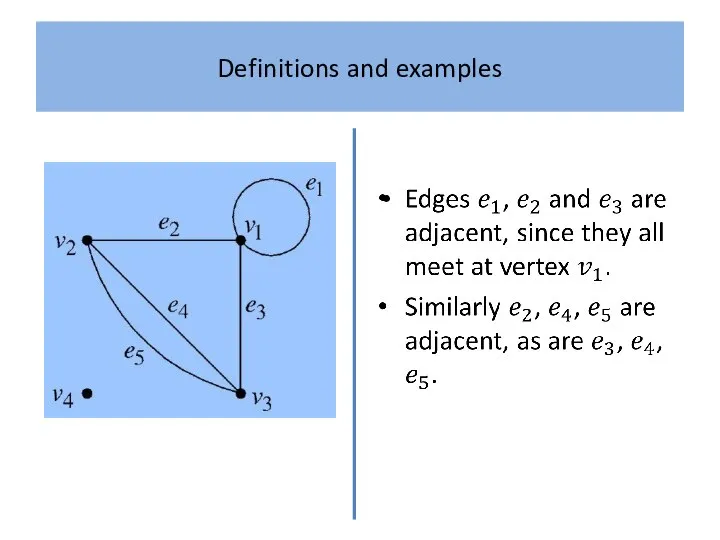
What is a ‘graph’? Intuitively, a graph is simply a collection of points, called ‘vertices’, and a collection of lines, called ‘edges’, each of which joins either a pair of points or a single point to itself.
A familiar example, which serves as a useful analogy, is a road map which shows towns as vertices and the roads joining them as edges.

Definitions and examples

Definitions and examples

Definitions and examples

Definitions and examples

Definitions and examples

Definitions and examples
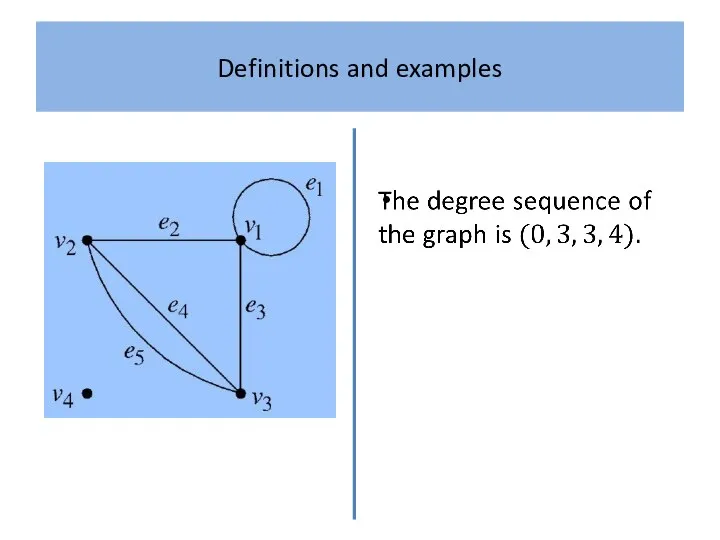
Definition 2
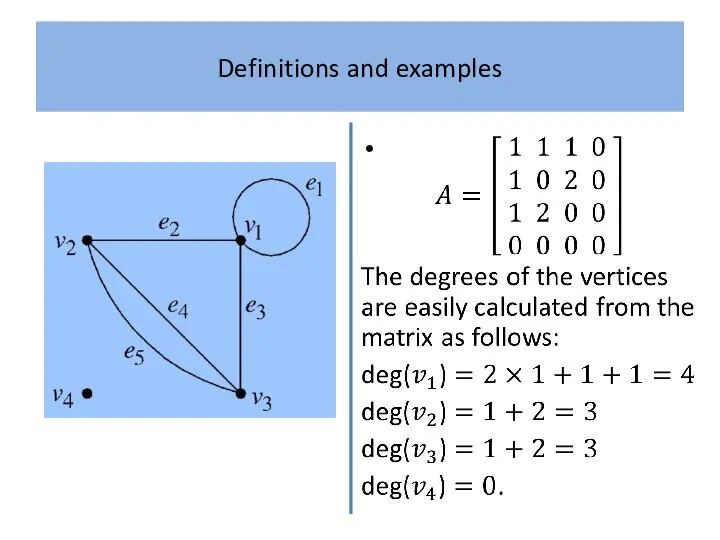
The degree sequence of a graph is the sequence of its vertex degrees arranged in non-decreasing order.

Definitions and examples

Definitions and examples

Definitions and examples
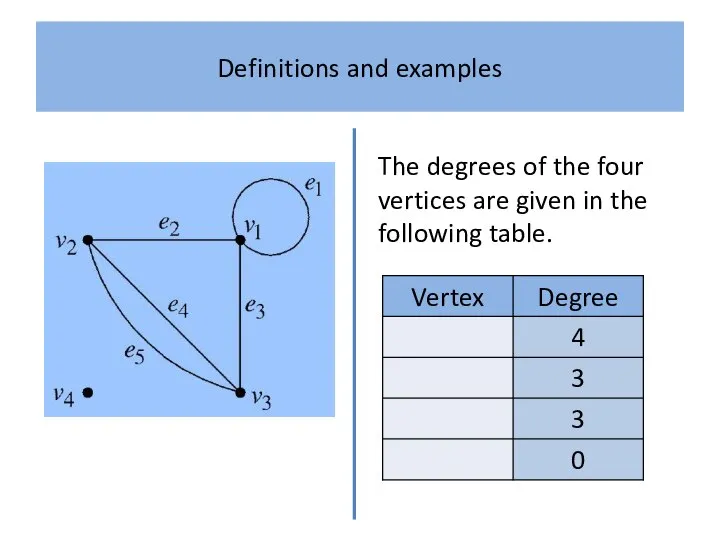
The degrees of the four vertices are given in the following table.

Definitions and examples

Definitions and examples
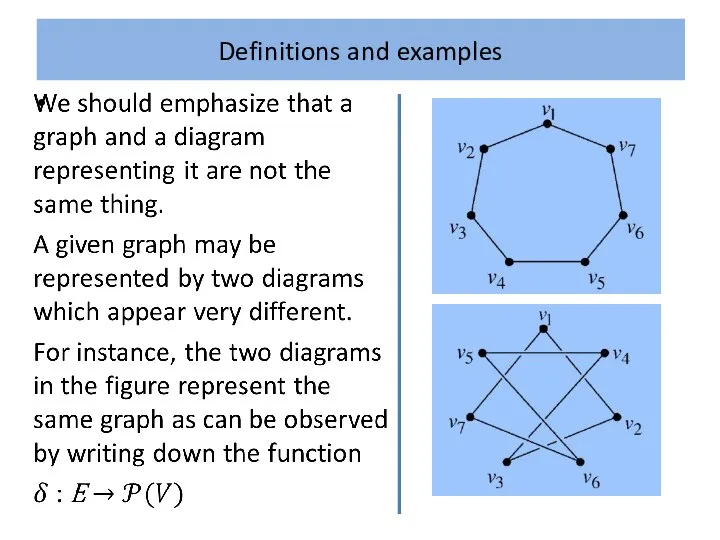
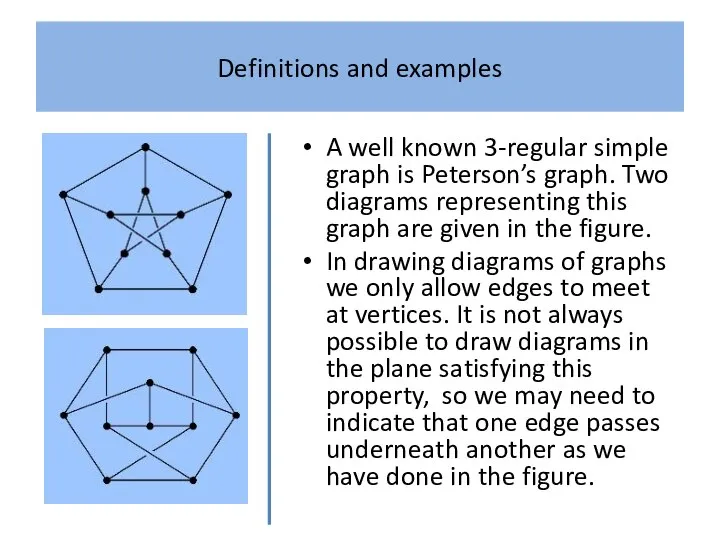
A well known 3-regular simple graph is Peterson’s graph. Two diagrams representing this graph are given in the figure.
In drawing diagrams of graphs we only allow edges to meet at vertices. It is not always possible to draw diagrams in the plane satisfying this property, so we may need to indicate that one edge passes underneath another as we have done in the figure.

Definitions and examples

Definitions and examples
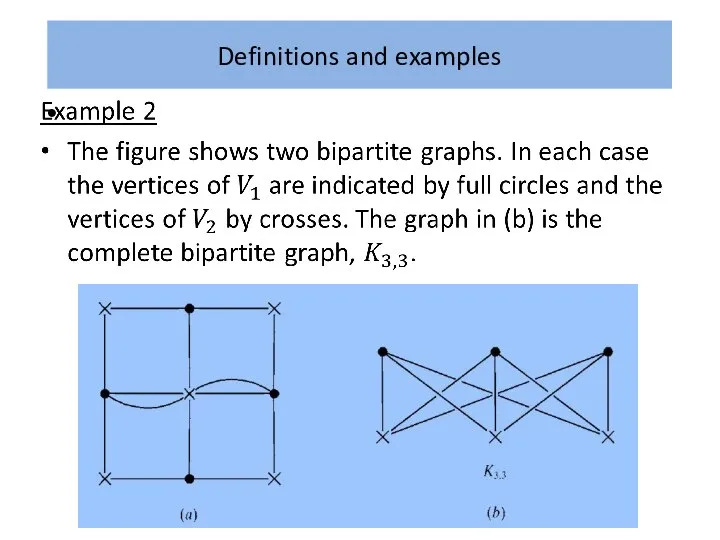
Example 1
Since a complete graph is simple there are no loops and each pair of distinct vertices is joined by a unique edge. Clearly a complete graph is uniquely specified by the number of its vertices.

Definitions and examples

Definitions and examples
Example 1
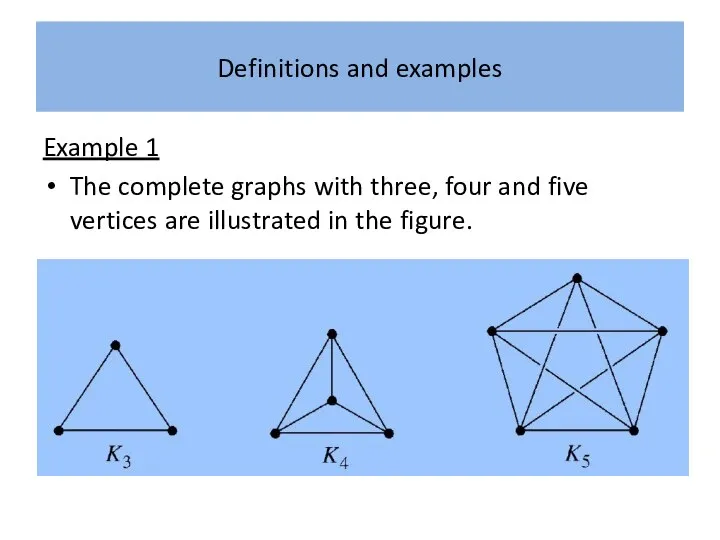
The complete graphs with three, four and five vertices are illustrated in the figure.

Definitions and examples

Definitions and examples

Definitions and examples

Definitions and examples

Definitions and examples

Definitions and examples

Definitions and examples

Definitions and examples

Definitions and examples

Definitions and examples

Definitions and examples

Definitions and examples
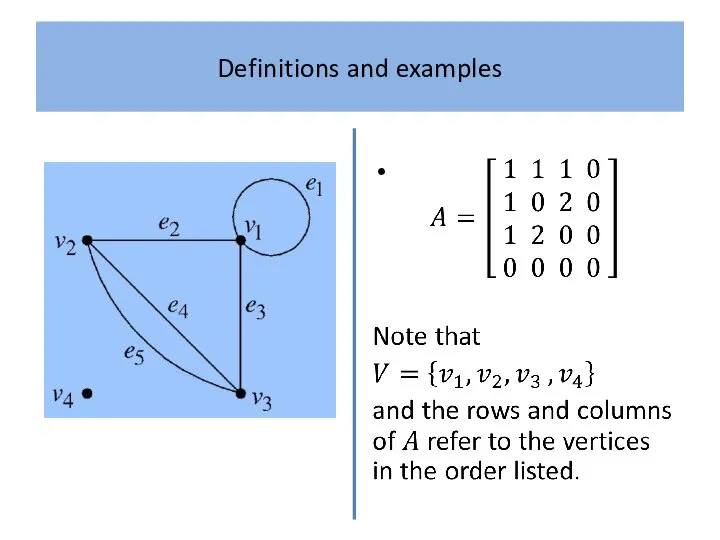
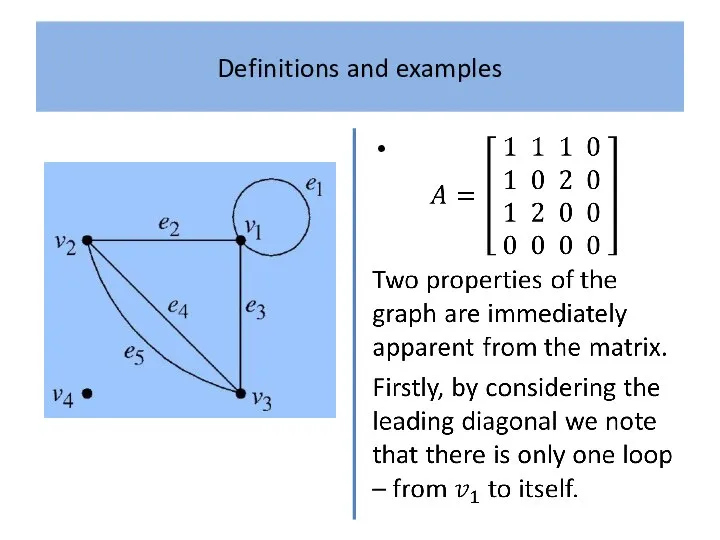
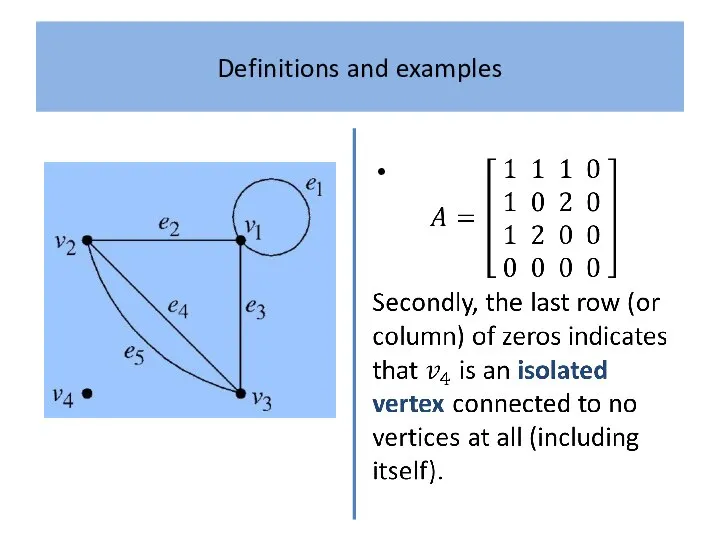
Example 4
A complete graph has adjacency matrix with zeros along the leading diagonal (since there are no loops) and ones everywhere else (since every vertex is joined to every other by a unique edge).

Definitions and examples

Definitions and examples

Paths and cycles
Using the analogy of a road map, we can consider various types of ‘journeys’ in a graph.
For instance, if the graph actually represents a network of roads connecting various towns, one question we might ask is: is there a journey, beginning and ending at the same town, which visits every other town just once without traversing the same road more than once?
As usual, we begin with some definitions.

Paths and cycles

Paths and cycles

Paths and cycles

Paths and cycles
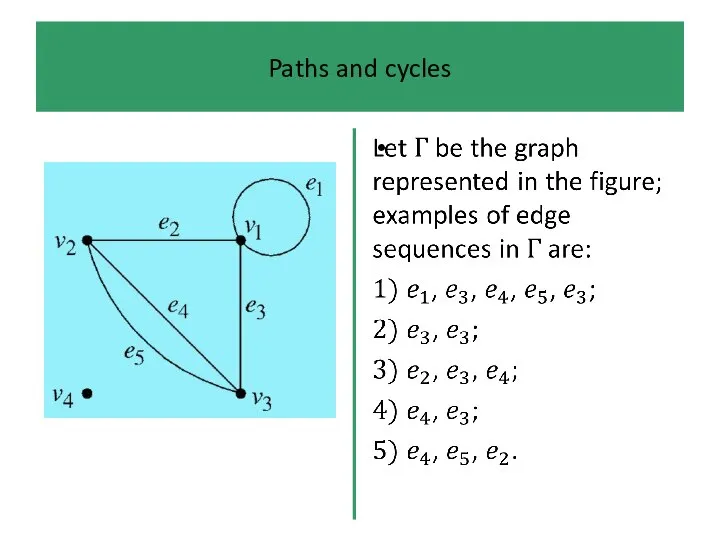
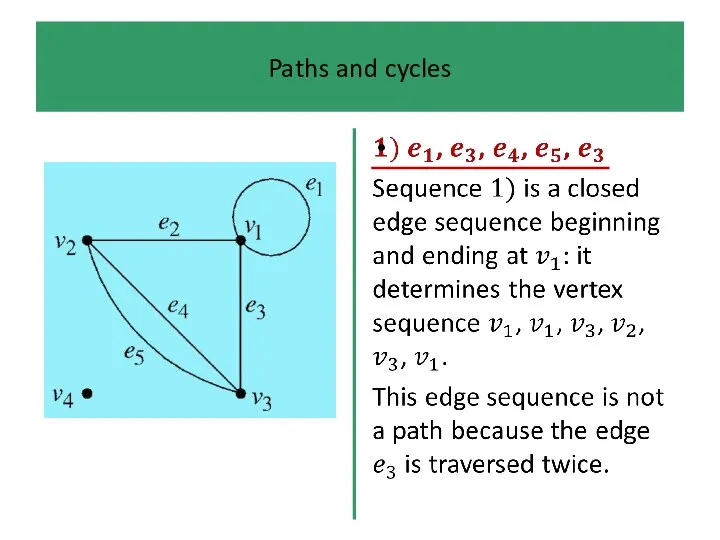
An edge sequence is any finite sequence of edges which can be traced on the diagram of the graph without removing pen from paper. It may repeat edges, go round loops several times, etc.

Paths and cycles
Edge sequences are too general to be of very much use which is why we have defined paths.

Paths and cycles
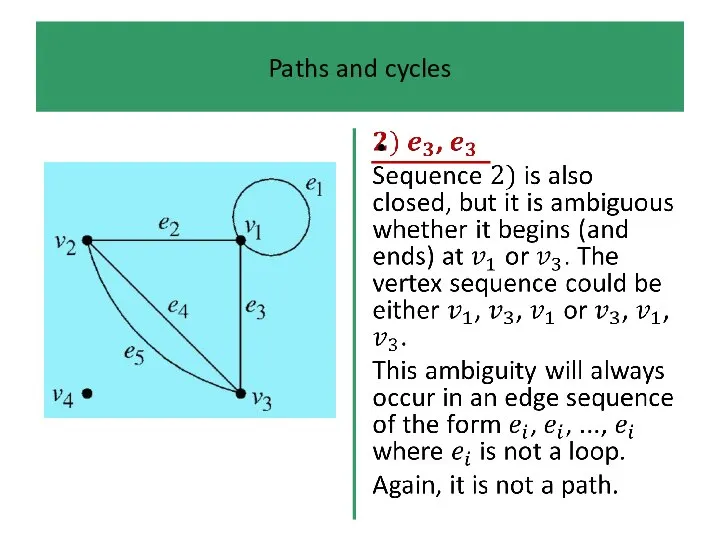
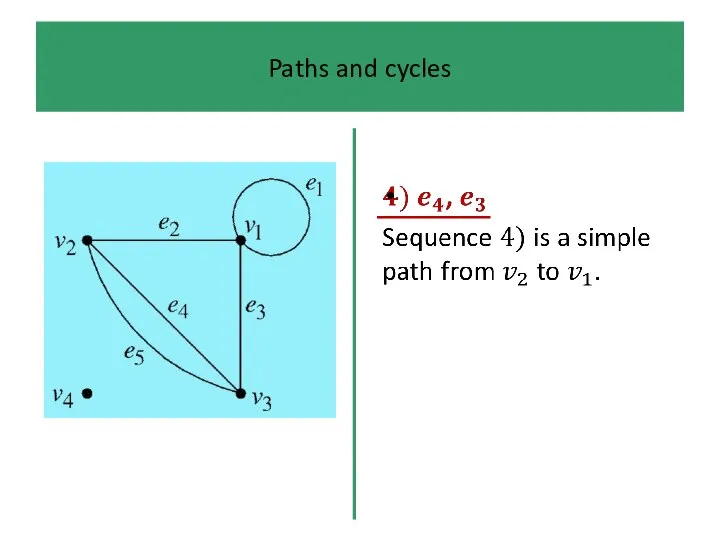
In a path we are not allowed to ‘travel along’ the same edge more than once.

Paths and cycles
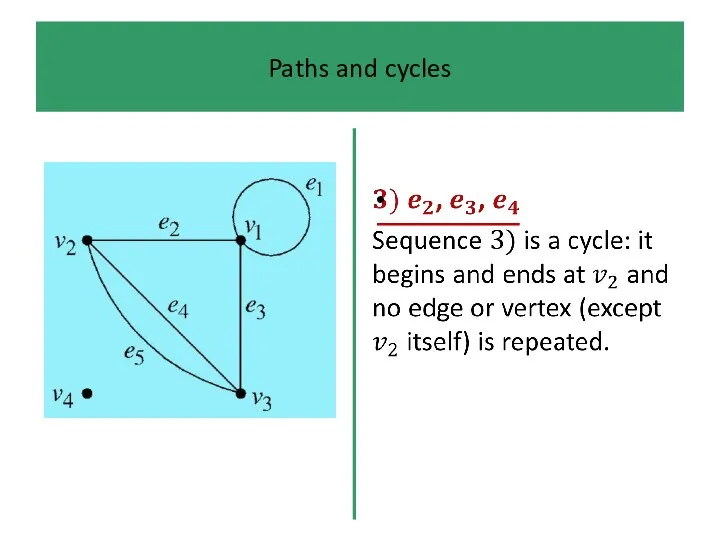
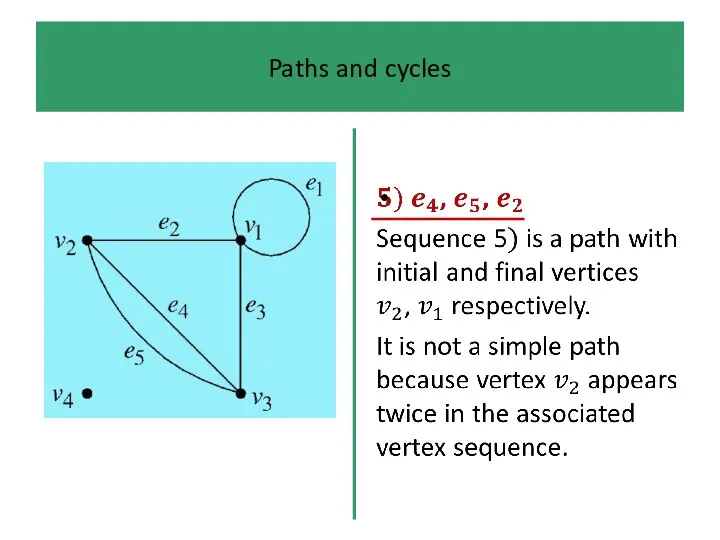
If, in addition, we do not ‘visit’ the same vertex more than once (which rules out loops), then the path is simple.

Paths and cycles
The edge sequence or path is closed if we begin and end the ‘journey’ at the same place.

Paths and cycles

Paths and cycles

Paths and cycles

Paths and cycles

Paths and cycles

Paths and cycles

Paths and cycles
In an intuitively obvious sense, some graphs are ‘all in one piece’ and others are made up of several pieces.
We can use paths to make this idea more precise.

Paths and cycles
Definition 7
A graph is connected if, given any pair of distinct vertices, there exists a path connecting them.

Paths and cycles
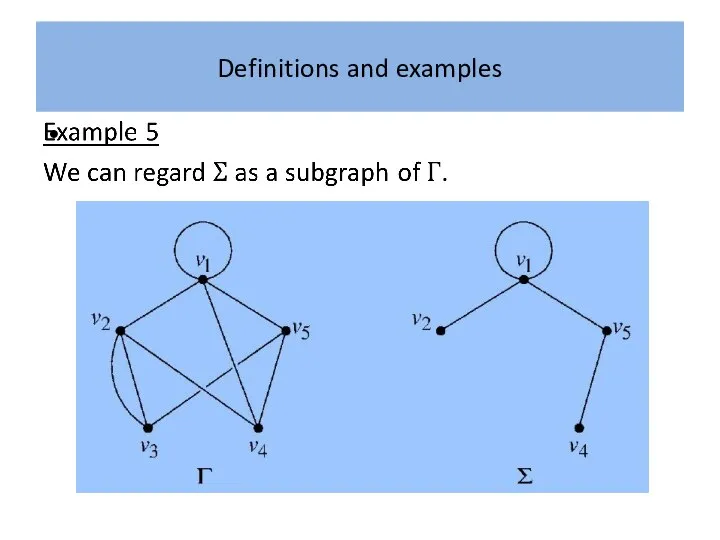
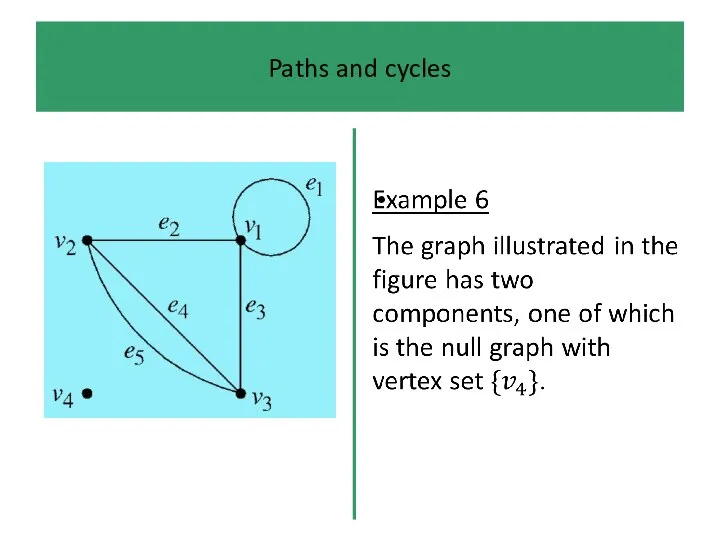
An arbitrary graph naturally splits up into a number of connected subgraphs, called its (connected) components.
The components can be defined formally as maximal connected subgraphs.

Paths and cycles

Paths and cycles
The components of a graph are just its connected ‘pieces’.
In particular, a connected graph has only one component.
Decomposing a graph into its components can be very useful.
It is usually simpler to prove results about connected graphs and properties of arbitrary graphs can frequently then be deduced by considering each component in turn.

Paths and cycles