Методы сортировки. Алгоритмы методов простого выбора, пузырька, сортировки расческой, быстрой сортировки

Метод простого выбора.
Метод заключается в последовательном нахождении минимального или максимального элемента (в зависимости от того сортируем ли мы массив по возрастанию или по убыванию) и перестановке его в начало массива.
for (k = 0; k < N - 1; k++) {
// нахождение индекса минимального элемента
ind_max = k;
for (i = 1 + k; i < N; i++)
if (arr[i] > arr[ind_max]) ind_max = i;
// обмен элементов
temp = arr[k];
arr[k] = arr[ind_max];
arr[ind_max] = temp;
}

ind_max – индекс текущего максимального элемента;
k – индекс элемента, который обменивается с максимальным элементом.
На первом шаге мы должны поставить максимальный элемент всего массива на место 1го элемента. То есть поменять arr[0] и arr[ind_max].
Далее мы ищем новый максимальный элемент в хвостовой части массива (не учитывая arr[0]) и меняем его местами со вторым элементом массива.
То есть меняем arr[1] и arr[ind_max].
Далее снова ищем максимальный элемент в хвостовой части массива (не учитывая arr[0] и arr[1]) и меняем его с третьим элементом. То есть меняем arr[2] и arr[ind_max].
Далее продолжаем находить максимальные элементы из хвостовой не отсортированной части массива и менять их с первым не отсортированным элементом пока не достигнем предпоследнего элемента.
Описание алгоритма метода простого выбор

Метод пузырька.
Сортировка методом пузырька предполагает многократное прохождение по массиву и обмен рядом стоящих элементов массива в том случае, если эти элементы стоят в неверном порядке. В нашем случае, переменная count будет отвечать за количество обменов, совершенных при прохождении вдоль массива. Эта переменная обнуляется, затем происходит обход массива. Если во время обхода был сделан хотя бы один обмен элементов местами, то count снова обнуляют и повторяют обход. Если же переменная после обхода массива осталась равной нулю, то значит, массив уже отсортирован.

int count = 1; //переменная для подсчета количества обменов
while (count > 0) {
//обнуление количества обменов
count = 0;
//прохождение по массиву
for (i = 0; i < N - 1; i++) {
if(arr[i] > arr[i + 1]) {
//обмен элементов
temp = arr[i];
arr[i] = arr[i + 1];
arr[i + 1] = temp;
//подсчет количества обменов count++;
}
}
}
Реализация метода

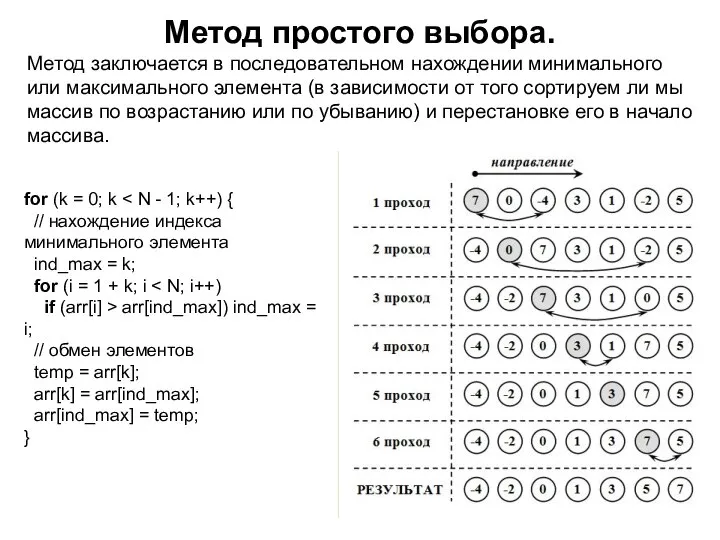
Возьмём массив с числами «5 1 4 2 8» и отсортируем значения по возрастанию, используя сортировку пузырьком. Выделены те элементы, которые сравниваются на данном этапе.
Наглядная демонстрация алгоритма.
Первый проход:
(5 1 4 2 8) (1 5 4 2 8), Здесь алгоритм сравнивает два первых элемента и меняет их местами.
(1 5 4 2 8) (1 4 5 2 8), Меняет местами, так как 5>4
(1 4 5 2 8) (1 4 2 5 8), Меняет местами, так как 5>2
(1 4 2 5 8) (1 4 2 5 8), Теперь, ввиду того, что элементы стоят на своих местах (8>5), алгоритм не меняет их местами.
Второй проход:
(1 4 2 5 8) (1 4 2 5 8)
(1 4 2 5 8) (1 2 4 5 8), Меняет местами, так как 4>2
(1 2 4 5 8) (1 2 4 5 8)
Теперь массив полностью отсортирован, но алгоритму это неизвестно. Поэтому ему необходимо сделать полный проход и определить, что перестановок элементов не было.
Третий проход:
(1 2 4 5 8) (1 2 4 5 8)
(1 2 4 5 8) (1 2 4 5 8)
Теперь массив отсортирован и алгоритм может быть завершён.
Пример работы алгоритма

Сортировка расчёской
Сортировка расчёской (англ. comb sort) — это довольно упрощённый алгоритм сортировки, изначально спроектированный Влодзимежом Добосевичем в 1980 г. Позднее он был переоткрыт и популяризован в статье Стивена Лэйси и Ричарда Бокса в журнале Byte Magazine в апреле 1991 г. Сортировка расчёской улучшает сортировку пузырьком, и конкурирует с алгоритмами, подобными быстрой сортировке.
В сортировке пузырьком, когда сравниваются два элемента, промежуток (расстояние друг от друга) равен 1. Основная идея сортировки расчёской в том, что этот промежуток может быть гораздо больше, чем единица

Программная реализация
double fakt = 1.2473309; // фактор уменьшения
double step = N - 1;
while (step >= 1){
for (i = 0; i + step < N; ++i) {
if (sort[i] > sort[i + step]) {
temp = sort[i + step];
sort[i + step] = sort[i];
sort[i] = temp;
}
}
step /= fakt;
}

Метод быстрой сортировки quick sort
Общая идея алгоритма состоит в следующем:
Выбрать из массива элемент, называемый опорным. Это может быть любой из элементов массива. От выбора опорного элемента не зависит корректность алгоритма, но в отдельных случаях может сильно зависеть его эффективность.
Сравнить все остальные элементы с опорным и переставить их в массиве так, чтобы разбить массив на три непрерывных отрезка, следующие друг за другом: «меньшие опорного», «равные» и «большие».
Для отрезков «меньших» и «больших» значений выполнить рекурсивно ту же последовательность операций, если длина отрезка больше единицы.
На практике массив обычно делят не на три, а на две части: например, «меньшие опорного» и «равные и большие»; такой подход в общем случае эффективнее, так как упрощает алгоритм разделения

Алгоритм
Выбрать элемент из массива. Назовём его опорным.
Разбиение: перераспределение элементов в массиве таким образом, что элементы меньше опорного помещаются перед ним, а больше или равные после.
Рекурсивно применить первые два шага к двум подмассивам слева и справа от опорного элемента. Рекурсия не применяется к массиву, в котором только один элемент или отсутствуют элементы.