Информатика, энтропия, кодирование

То, что событие случайно, означает отсутствие полной уверенности в его наступлении, что, в свою очередь, создает неопределенность в исходах опытов, связанных с данным событием. Безусловно, степень неопределенности различна для разных ситуаций.
Для практики важно иметь возможность произвести численную оценку неопределенности разных опытов. Попробуем ввести такую количественную меру неопределенности
Энтропия
Рассмотри опыт с п равновероятных исходов. Очевидно, что неопределенность каждого из них зависит от n, т.е. мера неопределенности является функцией числа исходов f(n).
Можно указать некоторые свойства этой функции:
f(1) = 0, поскольку при п = 1 исход опыта не является случайным и, следовательно, неопределенность отсутствует;
f(n) возрастает с ростом п, поскольку чем больше число возможных исходов, тем более затруднительным становится предсказание результата опыта.
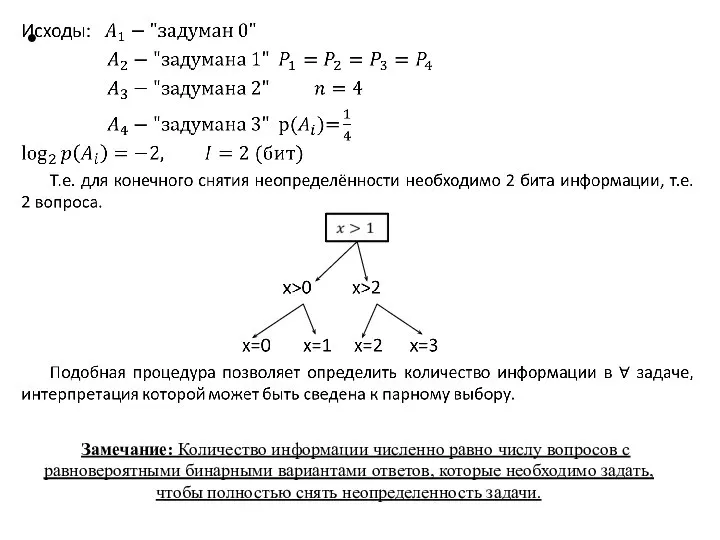
Энтропия как мера неопределенности

Для определения явного вида функции f(n) рассмотрим два независимых опыта α и β с количествами равновероятных исходов, соответственно пα и пβ.
Пусть имеет место сложный опыт, который состоит в одновременном выполнении опытов α и β; число возможных его исходов равно пα ∙ пβ, причем, все они равновероятны.
Очевидно, неопределенность исхода такого сложного опыта α ^ β будет больше неопределенности опыта α, поскольку к ней добавляется неопределенность β;
мера неопределенности сложного опыта равна f(nα ∙ nβ). С другой стороны, меры неопределенности отдельных α и β составляют, соответственно, f(nα) и f(nβ).
В первом случае (сложный опыт) проявляется общая (суммарная) неопределенность совместных событий, во втором - неопределенность каждого из событий в отдельности. Однако из независимости α и β следует, что в сложном опыте они никак не могут повлиять друг на друга и, в частности, α не может оказать воздействия на неопределенность β, и наоборот.

Следовательно, мера суммарной неопределенности должна быть равна сумме мер неопределенности каждого из опытов, т.е. мера неопределенности аддитивна:
f(nα ∙ nβ). = f(пα) + f(пβ)
За меру неопределенности опыта с п равновероятными исходами можно принять число log(n).
То есть
f(n) = log (n) (1)
Следует заметить, что выбор основания логарифма в данном случае значения не имеет, поскольку в силу известной формулы преобразования логарифма от одного основания к другому (logbn=logba*logan)
Единица измерения неопределенности при двух возможных равновероятных исходах опыта называется бит.
Эта величина получила название энтропия. В дальнейшем будем обозначать ее Н.

Вновь рассмотрим опыт с n равновероятными исходами. Поскольку каждый исход случаен, он вносит свой вклад в неопределенность всего опыта, но так как все n исходов равнозначны, разумно допустить, что и их неопределённости одинаковы.
Из свойства аддитивности неопределенности, а также того, что согласно (1) общая неопределенность равна log2n, следует, что неопределенность, вносимая одним исходом составляет:
Таким образом, неопределенность, вносимая каждым из равновероятных исходов, равна:

Теперь попробуем обобщить формулу (2) на ситуацию, когда исходы опытов неравновероятны, например, р(А1) и р(А2). Тогда:
Введенная таким образом величина называется энтропией опыта α.
Энтропия является мерой неопределенности опыта, в котором проявляются случайные события, и равна средней неопределенности всех возможных его исходов.
Для практики формула (3) важна тем, что позволяет сравнить неопределенности различных опытов со случайными исходами.
(3)

Свойства энтропии
Энтропия сложного опыта, состоящего из нескольких независимых, равна сумме энтропии отдельных опытов.
В справедливости (4) можно убедиться непосредственно: Пусть опыт α имеет п исходов А1, А2, … Ап, которые реализуются с вероятностями р(А1), р(А2), ... р(Ап), а событие β - т исходов B1, В2, ... Вт с вероятностями р(В1), р(В2), ... р(Вт). Сложный опыт α ^ β имеет п∙т исходов типа AiBj (i = 1... n, j = 1... т). Следовательно:
(5)

Поскольку α и β - независимы, то независимыми окажутся события в любой паре Ai ^ Bj. Тогда, согласно Формулы условной вероятности,
В слагаемых произведено изменение порядка суммирования в соответствии со значениями индексов. Далее, по условию нормировки

Теперь рассмотрим ситуацию, когда имеются два опыта с одинаковым числом исходов п, но в одном случае они равновероятны, а в другом - нет. Каково соотношение энтропии опытов? Примем без доказательства следующее утверждение:

Условная энтропия
Найдем энтропию сложного опыта α ^ β в том случае, если опыты не являются независимыми, т.е. если на исход β оказывает влияние результат опыта α. Например, если в ящике всего два разноцветных шара и α состоит в извлечении первого, а β - второго из них, то а полностью снимает неопределенность сложного опыта α ^ β, т.е. оказывается Н(α ^ β) = H(α), a не сумме энтропии, как следует из (4).
Связь между α и β состоит в том, что какие-то из исходов A(α) могут оказывать влияние на исходы из В(β), т.е. некоторые пары событий Ai ∧ Bj не являются независимыми. Но тогда в (5) p(Ai ∧ Bj) следует заменять не произведением вероятностей, а:
При подстановке в (5) получаем:

Свойства условной энтропии

Энтропия и информация

Задача 1
Пусть опыт β состоит в извлечении одного шара из урны, содержащей 5 черных и 10 белых шаров, опыт αk - в предварительном извлечении из той же урны (без возвращения обратно) k шаров. Чему равна энтропия опыта β и информация об этом опыте, содержащаяся в опытах α1, α2, α3 и α4 ?

Замечание: Количество информации численно равно числу вопросов с равновероятными бинарными вариантами ответов, которые необходимо задать, чтобы полностью снять неопределенность задачи.

Свойства количества информации и энтропии