Прямой, обратный, дополнительный коды

Очень часто в вычислениях должны использоваться не только положительные, но и отрицательные числа.
Число со знаком в вычислительной технике представляется путем представления старшего разряда числа в качестве знакового. Принято считать, что 0 в знаковом разряде означает знак «плюс» для данного числа, а 1 – знак «минус».

Выполнение арифметических операций над числами с разными знаками представляется для аппаратной части довольно сложной процедурой.
В этом случае нужно определить большее по модулю число, произвести вычитание и присвоить разности знак большего по модулю числа.
Применение дополнительного кода позволяет выполнить операцию алгебраического суммирования и вычитания на обычном сумматоре. При этом не требуется определения модуля и знака числа.

Прямой код представляет собой одинаковое представление значимой части числа для положительных и отрицательных чисел и отличается только знаковым битом. В прямом коде число 0 имеет два представления «+0» и «–0».
Обратный код для положительных чисел имеет тот же вид, что и прямой код, а для отрицательных чисел образуется из прямого кода положительного числа путем инвертирования всех значащих разрядов прямого кода. В обратном коде число 0 также имеет два представления «+0» и «–0».

Дополнительный код для положительных чисел имеет тот же вид, что и прямой код, а для отрицательных чисел образуется путем прибавления 1 к обратному коду. Добавление 1 к обратному коду числа 0 дает единое представление числа 0 в дополнительном коде. Однако это приводит к асимметрии диапазонов представления чисел относительно нуля. Так, в восьмиразрядном представлении диапазон изменения чисел с учетом знака.
-128 <= x <= 127.

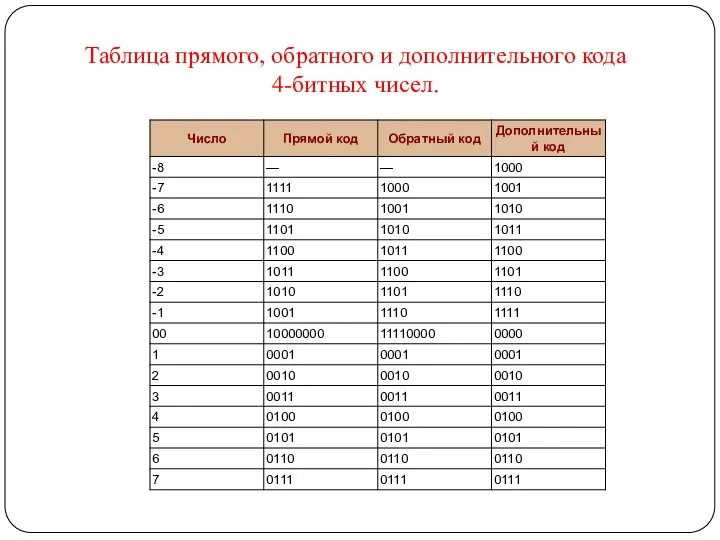
Таблица прямого, обратного и дополнительного кода
4-битных чисел.

Алгоритм получения дополнительного кода отрицательного числа.
Для получения дополнительного k-разрядного кода отрицательного числа необходимо
модуль отрицательного числа представить прямым кодом в k двоичных разрядах;
значение всех бит инвертировать: все нули заменить на единицы, а единицы на нули(таким образом, получается k-разрядный обратный код исходного числа);
к полученному обратному коду прибавить единицу.

Пример:
Получим 8-разрядный дополнительный код числа -52:
00110100 - число |-52|=52 в прямом коде
11001011 - число -52 в обратном коде
11001100 - число -52 в дополнительном коде

Домашняя работа

Правила сложения и вычитания чисел в двоичной системе счисления

Правила сложения
Пример
Сложить двоичные числа 11012 и 110112.
Запишем слагаемые в столбик и пронумеруем разряды, присвоив младшему разряду номер 1:
номера разрядов:
5 4 3 2 1
+ 1 1 0 1
1 1 0 1 1

Процесс образования результата по разрядам описан ниже:
1. разряд 1 формируется следующим образом: 1 + 1 = 10; 0 остается в разряде 1, 1 переносится во второй разряд;
2. разряд 2 формируется следующим образом: 0 + 1 + 1 = 10, где вторая 1 - единица переноса; 0 остается в разряде 2, 1 переносится в третий разряд;
3. третий разряд формируется следующим образом: 1 + 0 + 1 = 10, где вторая 1 - единица переноса; 0 остается в разряде 3, 1 переносится в разряд 4;
4. четвертый разряд формируется следующим образом: 1 + 1 + 1 = 11, где третья 1 - единица переноса; 1 остается в разряде 4, 1 переносится в пятый разряд;
5. пятый разряд формируется следующим образом: 1 + 1 = 10; где вторая 1 - единица переноса; 0 остается в разряде 5, 1 переносится в шестой разряд.

Таким образом:
1 1 0 1
+ 1 1 0 1 1
1 0 1 0 0 0

Проверим результат.
Для этого определим полные значения слагаемых и результата:
11012 = 1*23 +1*22 + 0*21 + 1*20 = 8 + 4 + 1 = 13;
110112 = 1*24 + 1*23 + 0*22 + 1*21 + 1*20 = 16 + 8 + 2 + 1 = 27;
1010002 = 1*25 + 0*24 + 1*23 + 0*22 + 0*21 + 0*21 = 32 + 8 = 40.
Поскольку 13 + 27 = 40, двоичное сложение выполнено верно.

Правила вычитания
Пример
Вычесть из двоичного числа 1012 двоичное число 112.
Запишем алгебраические слагаемые в столбик в порядке "уменьшаемое - вычитаемое" и пронумеруем разряды, присвоив младшему разряду номер 1:
номера разрядов:
3 2 1
- 1 0 1
1 1

Процесс образования результата по разрядам описан ниже:
1. разряд 1 формируется следующим образом: 1 - 1 = 0;
2. разряд 2 формируется следующим образом: поскольку 0 меньше 1 и непосредственное вычитание невозможно, занимаем для уменьшаемого единицу в старшем разряде 3. Тогда разряд 2 рассчитывается как 10 - 1 = 1;
3. третий разряд формируется следующим образом: поскольку единица была занята в предыдущем шаге, в разряде остался 0.

Таким образом:
1 0 1
- 1 1
1 0

Проверим результат.
Для этого определим полные значения слагаемых и результата. По таблице имеем::
1012 = 5;
112 = 3;
102 = 2.
Поскольку 5 - 3 = 2, вычитание выполнено верно.