Содержание
- 2. Использование нечеткой логики в экспертных системах Напомним, что нечеткую логику предложил Л.Заде, который распространил булеву логику
- 3. Особенности нечеткой логики В нечеткой логике определены эквиваленты операций И, ИЛИ и НЕ: p1 И p2
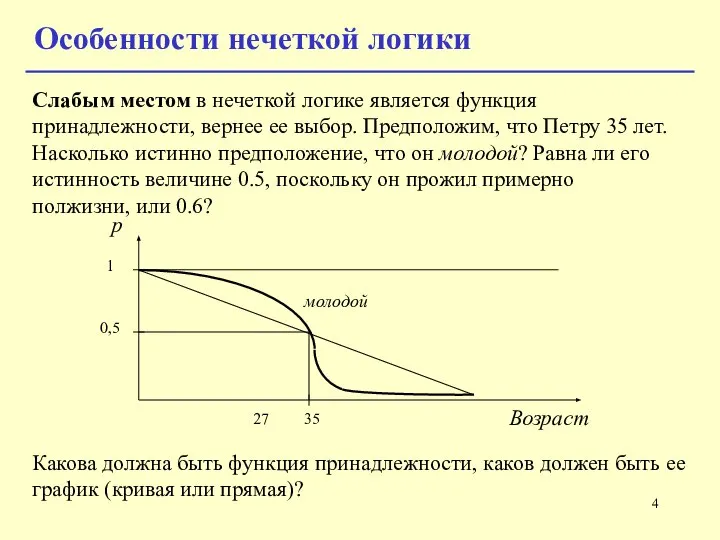
- 4. Слабым местом в нечеткой логике является функция принадлежности, вернее ее выбор. Предположим, что Петру 35 лет.
- 5. Для предпочтения одного вида функции другому нет серьезных рациональных обоснований, поэтому в реальной задаче могут присутствовать
- 6. Существует свыше десятка типовых форм кривых для задания функций принадлежности. Наибольшее распространение получили: треугольная, трапецеидальная и
- 7. Треугольная функция принадлежности определяется тройкой чисел (a,b,c), и ее значение в точке x вычисляется согласно выражению:
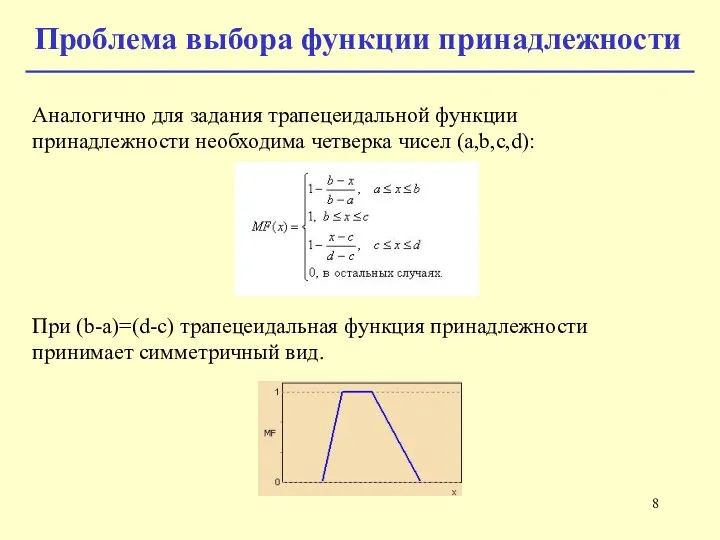
- 8. Аналогично для задания трапецеидальной функции принадлежности необходима четверка чисел (a,b,c,d): При (b-a)=(d-c) трапецеидальная функция принадлежности принимает
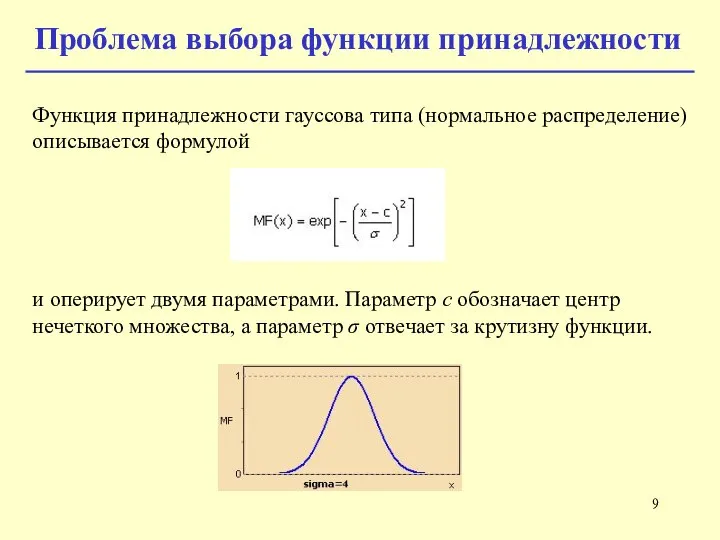
- 9. Функция принадлежности гауссова типа (нормальное распределение) описывается формулой и оперирует двумя параметрами. Параметр c обозначает центр
- 10. Еще одной проблемой при использовании нечеткой логики является проблема взвешивания отдельных сведений и их использование в
- 11. Шортлифф (E. Shortliffe) разработал схему, основанную на так называемых коэффициентах уверенности, которые он ввел для измерения
- 12. Таким образом КУ – это простой способ взвешивания свидетельств «за» и «против». Заметим, что приведенная формула
- 13. Шортлифф ввел формулу уточнения для взвешивания свидетельств. Формула уточнения позволяет непосредственно сочетать новую информации со старыми
- 14. Формула (2) имеет два важных свойства: Она симметрична в том смысле, что порядок e1 и e2
- 15. Схема Шортлиффа. Формула уточнения Применяя формулу (2) получаем: МД [c : Правило 1, Правило 2] =
- 16. Схема Шортлиффа. Надежность правил Схема Шортлиффа допускает также возможность того, что правила, как и данные, могут
- 18. Скачать презентацию












 Правовые методы обеспечения информационной безопасности
Правовые методы обеспечения информационной безопасности История развития вычислительной техники
История развития вычислительной техники Bilgisayar аğları ve İletişim. (Hafta 3)
Bilgisayar аğları ve İletişim. (Hafta 3) Введение в язык С
Введение в язык С Информационные технологии на уроках
Информационные технологии на уроках Графика. Фигура из перекрытий
Графика. Фигура из перекрытий Программно-аппаратный комплекс мониторинга перемещений автотранспорта на территории торгово-ремонтного предприятия
Программно-аппаратный комплекс мониторинга перемещений автотранспорта на территории торгово-ремонтного предприятия History of the profession System administrator
History of the profession System administrator Форсаж 2018
Форсаж 2018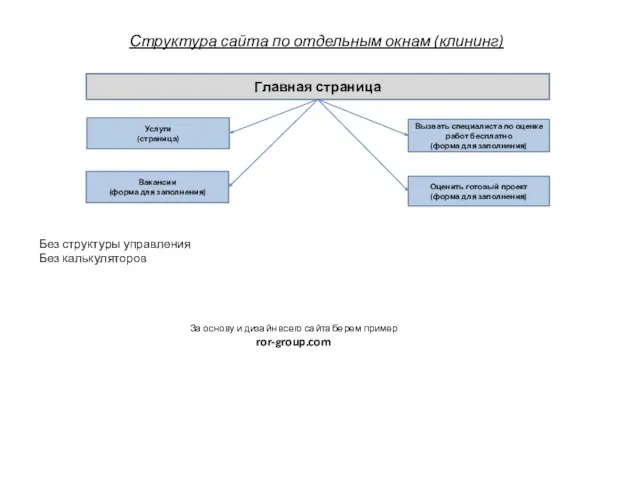 Структура сайта по отдельным окнам (клининг)
Структура сайта по отдельным окнам (клининг) История создания Интернета
История создания Интернета Решение задач с ветвлением
Решение задач с ветвлением Bit-Torrent
Bit-Torrent ВКР: Проектирование и разработка автоматизированных тестов для проекта кредитного конвейера
ВКР: Проектирование и разработка автоматизированных тестов для проекта кредитного конвейера MSE block library for Simulink
MSE block library for Simulink Организация вычислений в электронных таблицах
Организация вычислений в электронных таблицах Представление данных и машинные операции
Представление данных и машинные операции XML отчеты в BI Publisher
XML отчеты в BI Publisher Создание анимации
Создание анимации Формирование запроса для получения электронной подписи
Формирование запроса для получения электронной подписи Инфо-Импульс
Инфо-Импульс Моделі системи глобальної інформаційної безпеки
Моделі системи глобальної інформаційної безпеки Презентация11
Презентация11 Крауд маркетинг
Крауд маркетинг Построение геометрических примитивов. Привязки
Построение геометрических примитивов. Привязки Общение как обмен информацией
Общение как обмен информацией Система поиска автозапчастей
Система поиска автозапчастей Тема3_ОС_22
Тема3_ОС_22