Операции деления

Операция выполняется за n итераций и может быть описана следующим образом:
После п итераций получается
Частное от деления 2n-разрядного числа на n-разрядное может содержать более, чем п разрядов. В этом случае возникает переполнение, поэтому перед выполнением деления необходима проверка условия

-
Делению подвергаются целые числа в прямом коде. Z-слово, поэтому должно выполняться неравенство . Это возможно при ,
где
Для получения следует вычесть из ДМ делитель.
Если результат пробного вычитания >0, то и деление невозможно, если результат <0, то можно выполнить деление.

00100110 : 0101
0101 0111
1101<0пробное вычитание
0100
- 0101
1111<0
1001
- 0101 0100 >0
1001
0101
0100>0
1000
- 0101
0011>0
Пример ручного счета 38:5 =7 остаток 3
Z=X/Y
X-делимое, представляется целым числом удвоенной разрядности (2n) цифровых разрядов;
Y- делитель, представляемые словами, содержащими n- цифровых разрядов
Z-частное- представляемые словами, содержащими n- цифровых разрядов.

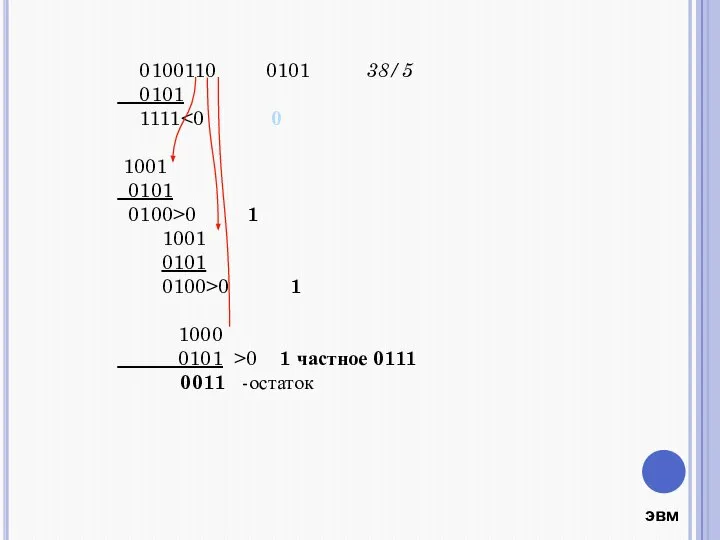
0100110 0101 38/5
0101
1111<0 0
1001
0101
0100>0 1 1001
0101
0100>0 1
1000
0101 >0 1 частное 0111
0011 -остаток

Алгоритм деления целых чисел с восстановлением остатка:
Числа представлены в прямом коде. Прием делимого и делителя.
Получение модулей, анализ знака.
3. Проверка на корректность деления: для целых чисел частное должно укладываться в разрядную сетку одинарной длины. Для дробных чисел делимое должно быть меньше делителя.
4. Исходное значение частичного остатка (промежуточные суммы ) полагается равным старшим разрядам делимого. Частичный остаток удваивается путем сдвига на 1 разряд влево. При этом в высвободившийся младший разряд частичного остатка заносится очередная цифра делимого.
5. Производится вычитание делителя (прибавление в дополнительном коде ) и анализ полученного остатка. Если частичный остаток меньше 0, то цифра частного равна 0 и в этом же такте производится восстановление остатка прибавлением делителя. Если частичный остаток больше 0, то очередная цифра частного равна 1. Такая последовательность действий повторяется до получения всех цифр модуля частного.
6. Пункты 4-5 последовательно выполняются для получения всех цифр модуля частного.
7.Знак частного формируется отдельно; при реализации алгоритма выполняется проверка делимого на 0 и делителя на 0.

41/6=6(5)
0010 1001 :0110 0110=+6
0101 001* 1010=-6
+1010
1111 0010 ЧАСТИЧНЫЙ ОСТАТОК<0
+0110такт восстановления
0101 0010_
1010 010*
+1010
0100 0101>0
1000 101*
+1010
0010 101* >0
0101 011*
+1010
1111 0110<0
+ 0110-такт восстановления
0101- остаток

Приведем алгоритм деления без восстановления остатка
Исходное значение частичного остатка полагается равным старшим разрядам делимого.
Частичный остаток удваивается путем сдвига на один разряд влево. При этом в освобождающийся при сдвиге младший разряд ЧО заносится очередная цифра частного.
Из сдвинутого частичного остатка вычитается делитель, если остаток положителен, и к сдвинутому частичному остатку прибавляется делитель, если остаток отрицательный.
На каждом шаге содержимое регистра делимого (РгДМ) и регистра частного (РгЧ) сдвигается на один разряд влево.
В зависимости от сочетания знаков частичного остатка и делителя определяется значение очередной цифры частного и требуемое действие: вычитание или прибавление делителя.
Вычитание делителя производится посредством прибавления дополнительного кода делителя. Преобразование в дополнительный код осуществляется за счет передачи делителя на вход сумматора обратным (инверсным) кодом с последующим добавлением единицы к младшему разряду сумматора.
Данная процедура повторяется для всех цифр делимого, о чем свидетельствует нулевое содержимое счетчика циклов(исходное значение СЧЦ равно разрядности делителя). Содержимое СЧЦ уменьшается на единицу после каждой итерации.
По окончании операции деления частное располагается в регистре частного, а в регистре делимого будет остаток от деления.
На заключительном этапе, если это необходимо, производится корректировка полученного результата, как это предусматривает алгоритм деления чисел со знаком
*На практике для накопления и хранения частного вместо отдельного регистр используют освобождающиеся в процессе сдвигов младшие разряды регистра делимого.

Особенности алгоритма деления c неподвижным делителем без восстановления остатка, для чисел представленных в прямом коде.
Отличие от предыдущего алгоритма:
-если знак частичного остатка больше 0, то выполняется вычитание делителя,
- если знак частичного остатка меньше 0, то производится прибавление делителя.
Представленная на рисунке структура АЛУ используется для деления чисел на сумматоре прямого и дополнительного кодов. При использовании прямого кода в структуру вводят триггеры для хранения знаков.
5:2=2(1)
000101 010=+2 ; 110=-2
00101_
+110
111010
11010_
+010
000101
00101_
+110
111010
частное
Остаток в доп. Коде 111доп.код=001 в прямом коде

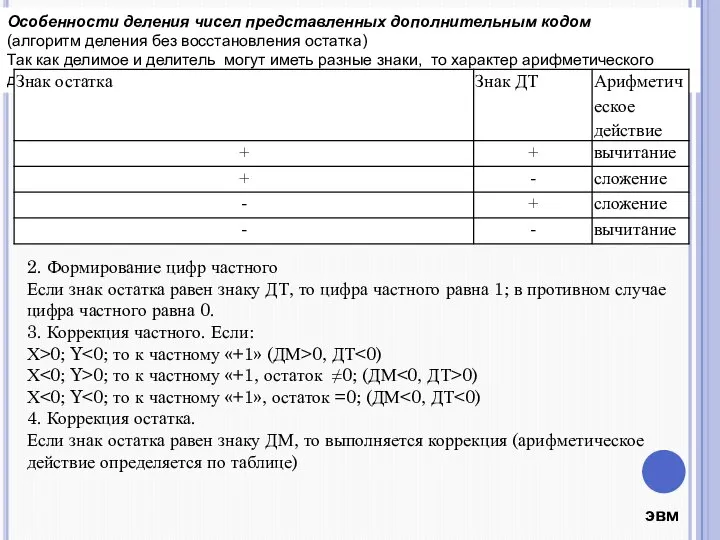
Особенности деления чисел представленных дополнительным кодом
(алгоритм деления без восстановления остатка)
Так как делимое и делитель могут иметь разные знаки, то характер арифметического действия определяется по таблице 10.
2. Формирование цифр частного
Если знак остатка равен знаку ДТ, то цифра частного равна 1; в противном случае цифра частного равна 0.
3. Коррекция частного. Если:
Х>0; Y<0; то к частному «+1» (ДМ>0, ДТ<0)
Х<0; Y>0; то к частному «+1, остаток ≠0; (ДМ<0, ДТ>0)
Х<0; Y<0; то к частному «+1», остаток =0; (ДМ<0, ДТ<0)
4. Коррекция остатка.
Если знак остатка равен знаку ДМ, то выполняется коррекция (арифметическое действие определяется по таблице)

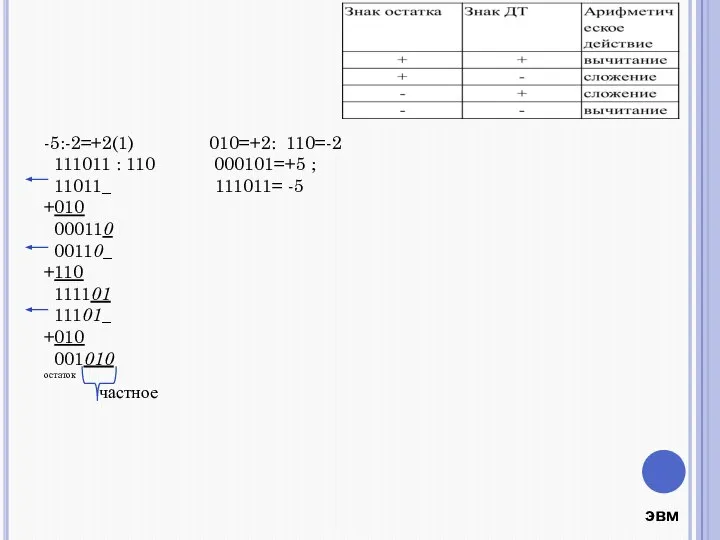
-5:-2=+2(1) 010=+2: 110=-2
111011 : 110 000101=+5 ;
11011_ 111011= -5
+010
000110 00110_
+110
111101
11101_
+010
001010
остаток
частное

Ускорить деление возможно, используя следующее:

Замена деления умножением на обратную величину
Операцию деления заменить на умножением
Основная задача - эффективное вычисление 1/у.
За­дача решается одним из двух методов; с помощью ряда Тейлора или метода Ньютона-Рафсона.
При реализации первого метода делитель ДТ представляется в виде: D = 1+Х. Тогда для двоичного представления D можно записать:
Возможные значения сомножителей в правой части выражения извлекались из таблицы емкостью 28 байт, хранящейся в памяти. Операция вычисления 1/D требует шести умножений.

Вычисление величины 1/D методом Ньютона-Рафсона сводится к нахождению корня уравнения
то есть Х= 1/D. Решение может быть получено с привлечением рекуррентного соотношения: Xi+l = Xi (2 –XiD).
Количество итераций определяется требуемой точностью вычисления X/D.
Реализация метода для n-разрядных чисел требует 2 int(log2n) - 1 операций умножения.
,

Ускорение вычисления частичных остатков
Возможности данного подхода весьма ограничены и связаны в основном с ускоре­нием операций сложения (вычитания). Способы достижения этой цели ничем не отличаются от тех, что применяются, например, при выполнении умножения. Это различные приемы для ускорения распространения переноса, матричные схемы сложения и т. п.

Алгоритм ускоренного деления SRT
Свое название алгоритм получил по фамилиям авторов (Sweeney, Robertson, Tocher), разработавших его независимо друг от друга приблизительно в одно и то же время.

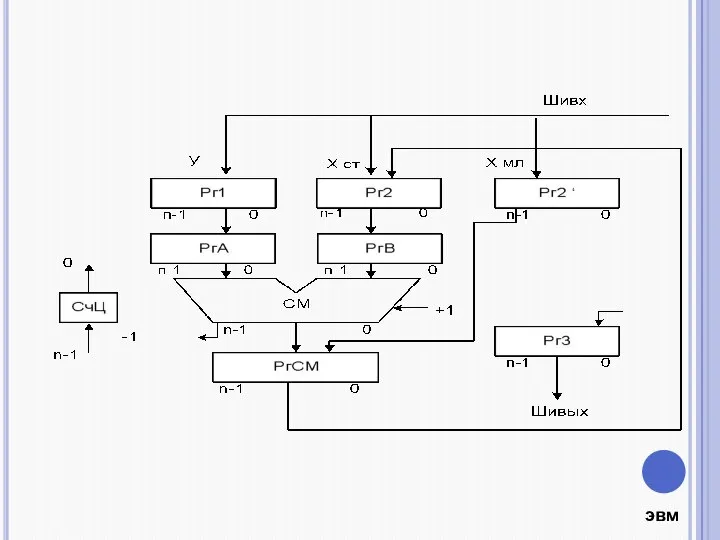
Делимое и делитель, представленные в дополнительном коде, размещаются в регистре делимого и делителя соответственно. Дальнейшие действия можно описать следующим образом.
1. Если в делителе D имеются k предшествующих нулей (при D > 0) или предшествующих единиц (при D< 0), то производится предварительный сдвиг содержимого РгДМ и РгДТвлево на к разрядов.
2. Для i от 0 до n-1:
если- три старших цифры частичного остатка в РгДМ совпадают, то qi =0 и производится сдвиг
содержимого РгДМ на один разряд влево;
если три старших цифры частичного остатка в РгДМ не совпадают, а сам ЧО отрицателен, то
qi =-l, делается сдвиг содержимого РгДМ на один разряд влево и к ЧО прибавляется делитель;
если три старших цифры частичного остатка в РгДМ не совпадают, а сам ЧО положителен, то qi = +1,выполняется сдвиг содержимого РгДМ на разряд влево и из ЧО вычитается делитель.
3. Если после завершения пункта 2 остаток отрицателен, то производится коррекция (к остатку прибавляется делитель, а из частного вычитается единица).
4. Остаток сдвигается вправо на к разрядов.

0.00101001 0.1001 +9
0 01010010 1.0111 -9
0 10100101
+1 0111
0 00010101
0 00101010 0 01010100
41/9
0.0000101001