Ключевые слова

Клод Шеннон (1916-2001). Его исследования позволили применить алгебру логики в вычислительной технике
Логика
Аристотель (384-322 до н.э.). Основоположник формальной логики (понятие, суждение, умозаключение).
Джордж Буль (1815-1864). Создал новую область науки - Математическую логику (Булеву алгебру или Алгебру высказываний).

Алгебра - наука об общих операциях, аналогичных сложению и умножению, которые могут выполняться над разнообразными математическими объектами – числами, многочленами, векторами и др.
Алгебра

Высказывание - это предложение на любом языке, содержание которого можно однозначно определить как истинное или ложное.
В русском языке высказывания выражаются повествовательными предложениями:
Земля вращается вокруг Солнца.
Москва - столица.
Побудительные и вопросительные предложения высказываниями не являются.
Без стука не входить!
Откройте учебники.
Ты выучил стихотворение?
Высказывание
Но не всякое повествовательное предложение является высказыванием:
Это высказывание ложное.

Высказывание или нет?
Зимой идет дождь.
Снегири живут в Крыму.
Кто к нам пришел?
У треугольника 5 сторон.
Как пройти в библиотеку?
Переведите число в десятичную систему.
Запишите домашнее задание

Алгебра логики определяет правила записи, вычисления значений, упрощения и преобразования высказываний.
В алгебре логики высказывания обозначают буквами и называют логическими переменными.
Если высказывание истинно, то значение соответствующей ему логической переменной обозначают единицей (А = 1), а если ложно - нулём (В = 0).
0 и 1 называются логическими значениями.
Алгебра логики

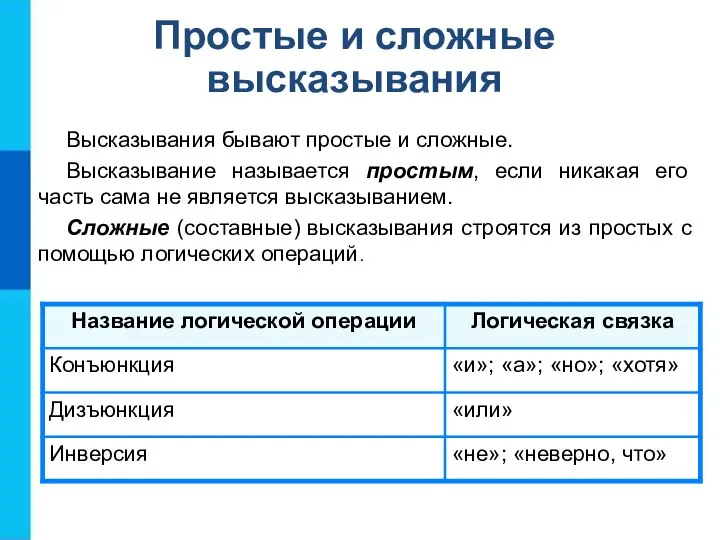
Простые и сложные высказывания
Высказывания бывают простые и сложные.
Высказывание называется простым, если никакая его часть сама не является высказыванием.
Сложные (составные) высказывания строятся из простых с помощью логических операций.

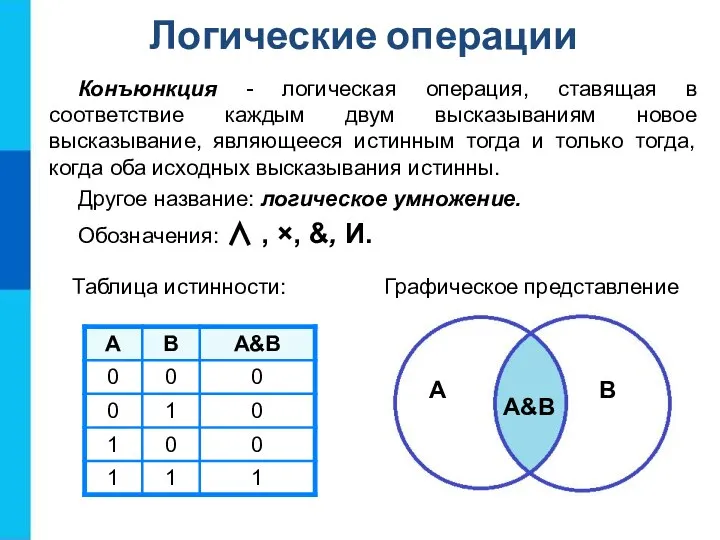
Конъюнкция - логическая операция, ставящая в соответствие каждым двум высказываниям новое высказывание, являющееся истинным тогда и только тогда, когда оба исходных высказывания истинны.
Другое название: логическое умножение.
Обозначения: ∧ , ×, &, И.
Логические операции
Таблица истинности:
Графическое представление
A
B
А&В

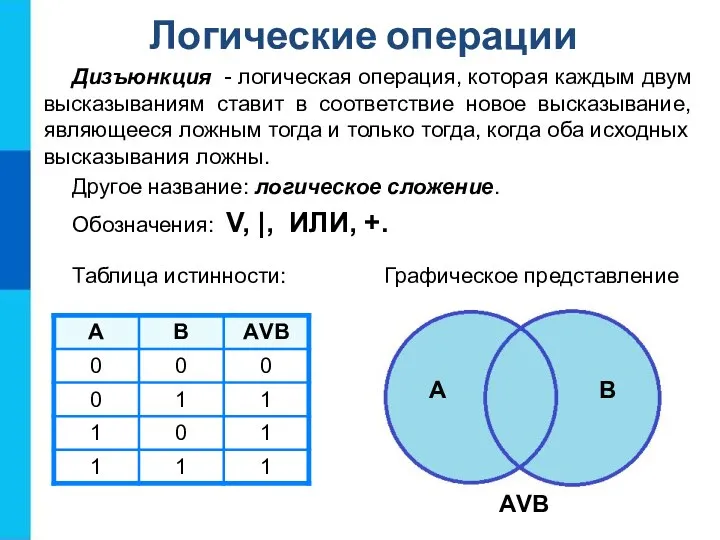
Дизъюнкция - логическая операция, которая каждым двум высказываниям ставит в соответствие новое высказывание, являющееся ложным тогда и только тогда, когда оба исходных высказывания ложны.
Другое название: логическое сложение.
Обозначения: V, |, ИЛИ, +.
Логические операции
Таблица истинности:
Графическое представление
A
B
АVВ

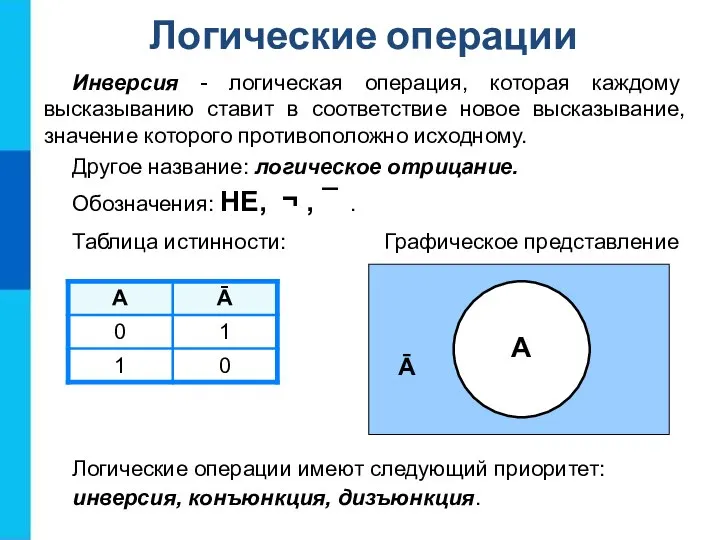
Инверсия - логическая операция, которая каждому высказыванию ставит в соответствие новое высказывание, значение которого противоположно исходному.
Другое название: логическое отрицание.
Обозначения: НЕ, ¬ , ¯ .
Логические операции имеют следующий приоритет:
инверсия, конъюнкция, дизъюнкция.
Логические операции
Таблица истинности:
Графическое представление
A
Ā

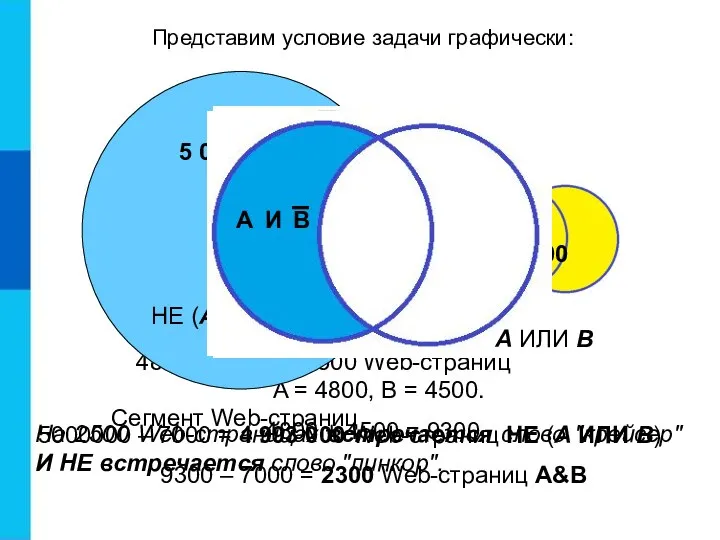
Пусть А = «На Web-странице встречается слово "крейсер"», В = «На Web-странице встречается слово "линкор"».
В некотором сегменте сети Интернет 5000000 Web-страниц. В нём высказывание А истинно для 4800 страниц, высказывание В - для 4500 страниц, а высказывание АVВ - для 7000 страниц.
Для какого количества Web-страниц в этом случае будут истинны следующие выражения и высказывание?
а) НЕ (А ИЛИ В);
б) А & B;
в) На Web-странице встречается слово "крейсер" И НЕ встречается слово "линкор".
Решаем задачу

5000000 – 7000 = 4 993 000 Web-страниц НЕ (А ИЛИ В) A = 4800, B = 4500.
4800 + 4500 = 9300
4800 – 2300 = 2500 Web-страниц
Представим условие задачи графически:
На 2500 Web-страницах встречается слово "крейсер" И НЕ встречается слово "линкор".
5 000 000
7 000
НЕ (А ИЛИ В)
Сегмент Web-страниц
A
B
A&B
9300 – 7000 = 2300 Web-страниц A&B
A
И
А ИЛИ В

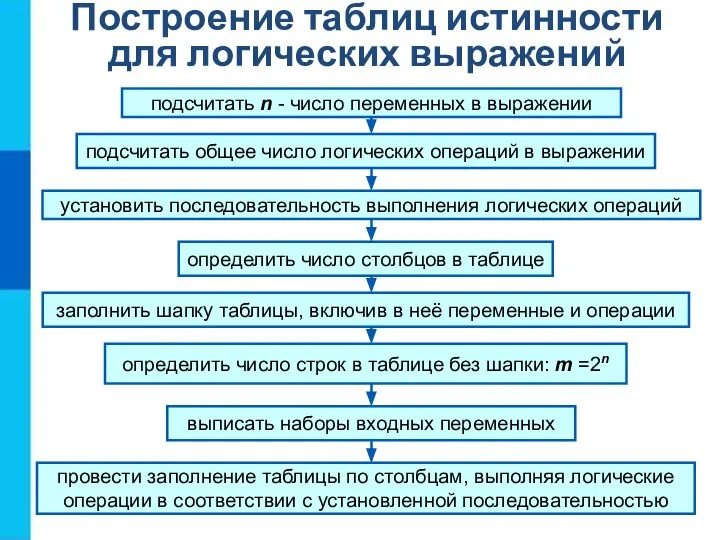
Построение таблиц истинности для логических выражений
подсчитать n - число переменных в выражении
подсчитать общее число логических операций в выражении
установить последовательность выполнения логических операций
определить число столбцов в таблице
заполнить шапку таблицы, включив в неё переменные и операции
определить число строк в таблице без шапки: m =2n
выписать наборы входных переменных
провести заполнение таблицы по столбцам, выполняя логические
операции в соответствии с установленной последовательностью

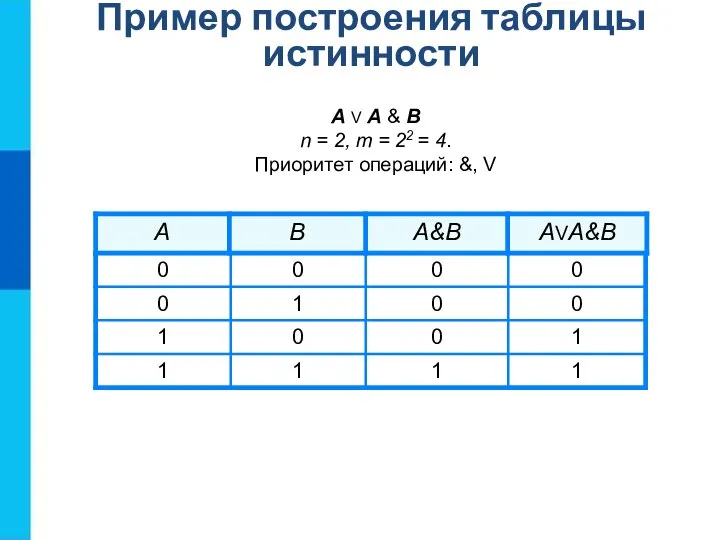
А V A & B
n = 2, m = 22 = 4.
Приоритет операций: &, V
Пример построения таблицы истинности

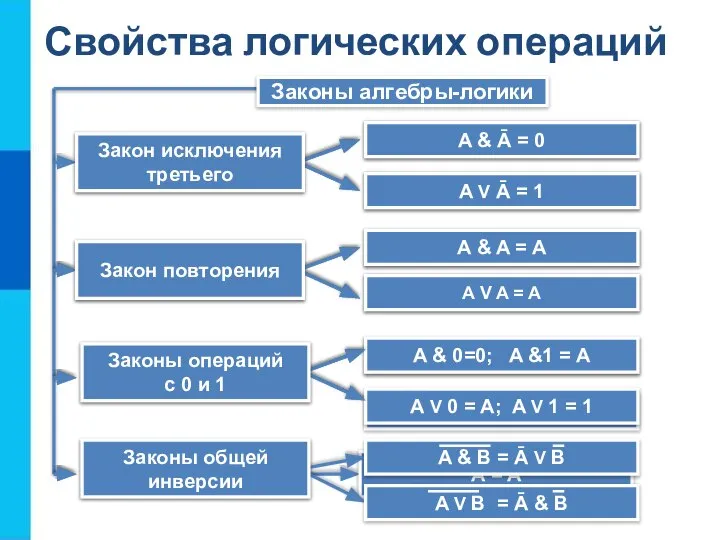
Свойства логических операций
Законы алгебры-логики
A & B = B & A
A V B = B V A
A&(BVC)= (A&B) V (A&C)
AV(B&C) = (AVB)&(AVC)
(A & B) & C = A & ( B & C)
(A V B) V C =A V ( B V C)
Переместительный
Сочетательный
Распределительный
Закон двойного
отрицания
A & Ā = 0
A V Ā = 1
A & 0=0; A &1 = A
A V 0 = A; A V 1 = 1
A & A = A
A V A = A
Закон исключения
третьего
Закон повторения
Законы операций
с 0 и 1
Законы общей
инверсии