Содержание
- 2. Вспоминаем то, что знаем
- 3. Определение подобных треугольников Первый признак подобия треугольников Отношение площадей подобных треугольников Начать изучение нового
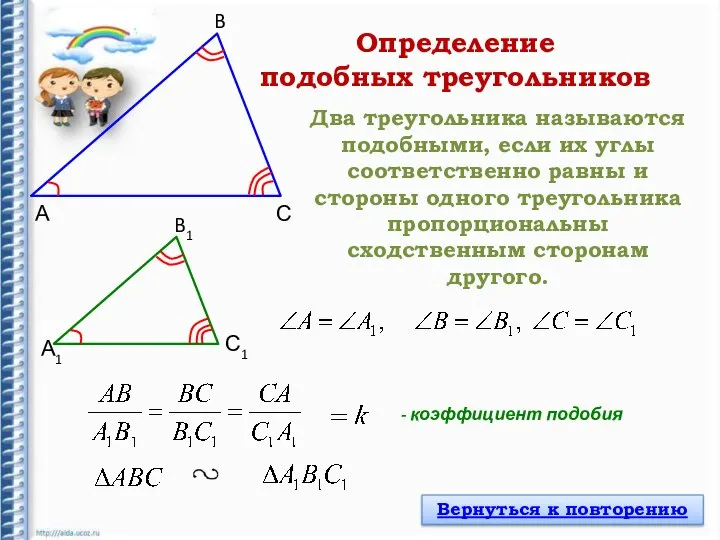
- 4. А B А1 B1 С С1 Два треугольника называются подобными, если их углы соответственно равны и
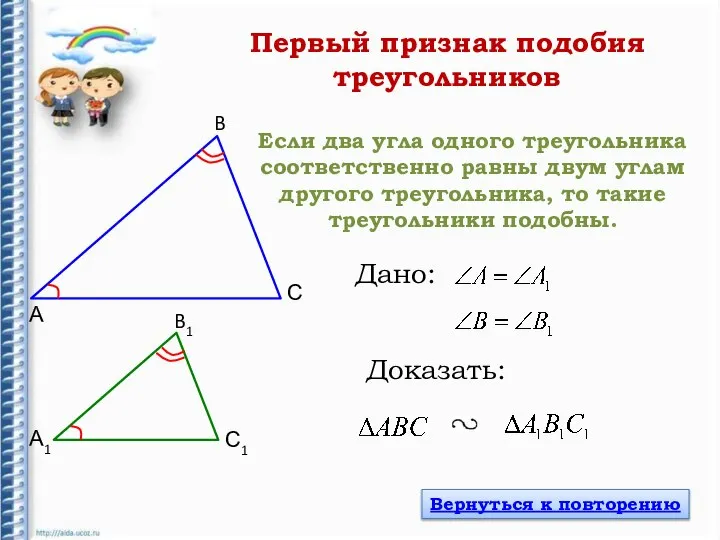
- 5. Если два угла одного треугольника соответственно равны двум углам другого треугольника, то такие треугольники подобны. А
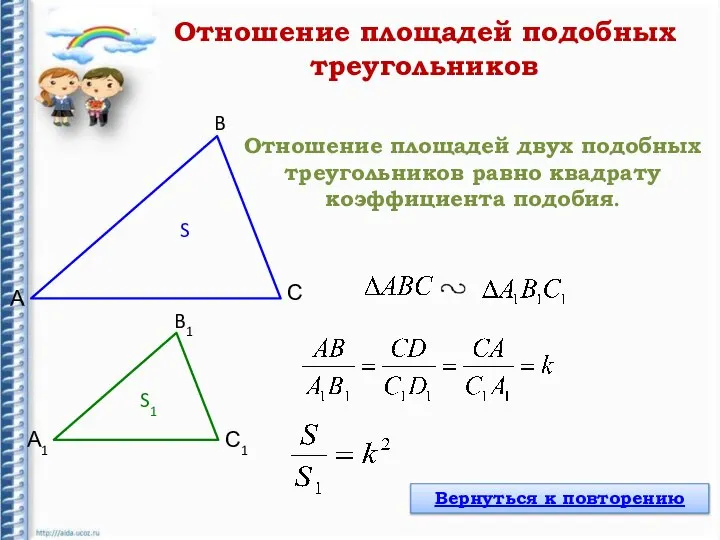
- 6. Отношение площадей двух подобных треугольников равно квадрату коэффициента подобия. А B А1 B1 С С1 S
- 7. Открываем новые знания
- 8. Второй признак подобия треугольников Третий признак подобия треугольников Начать развивать умения
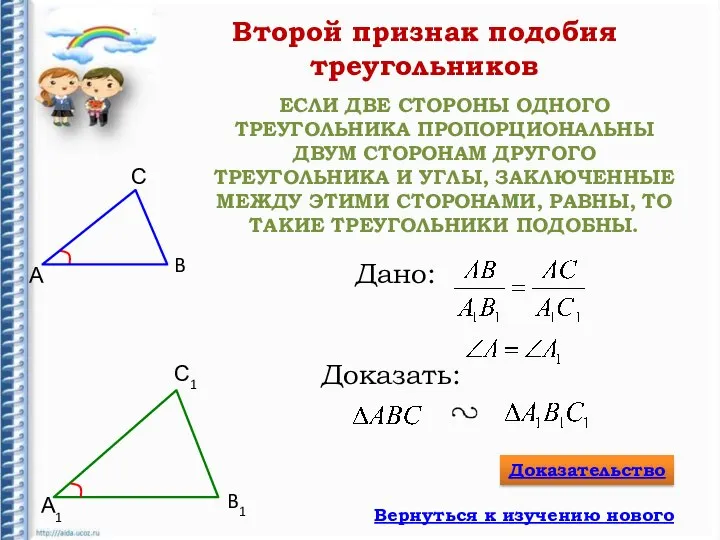
- 9. ЕСЛИ ДВЕ СТОРОНЫ ОДНОГО ТРЕУГОЛЬНИКА ПРОПОРЦИОНАЛЬНЫ ДВУМ СТОРОНАМ ДРУГОГО ТРЕУГОЛЬНИКА И УГЛЫ, ЗАКЛЮЧЕННЫЕ МЕЖДУ ЭТИМИ СТОРОНАМИ,
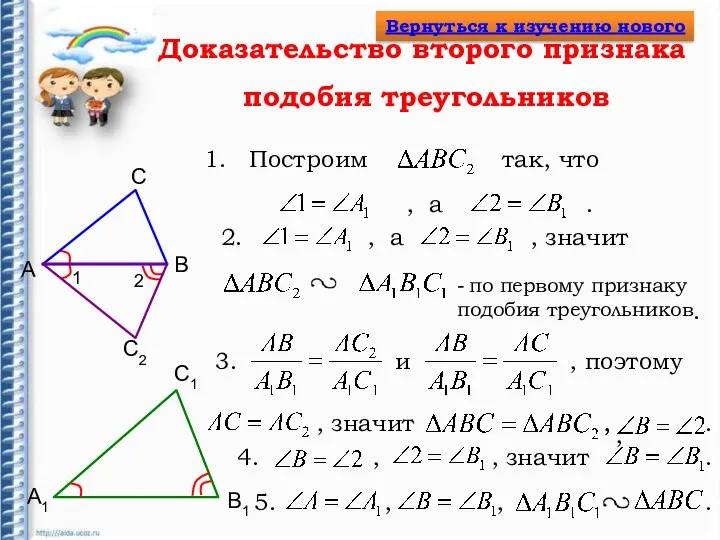
- 10. Доказательство второго признака подобия треугольников А B А1 B1 С С1 С2 1 2 - по
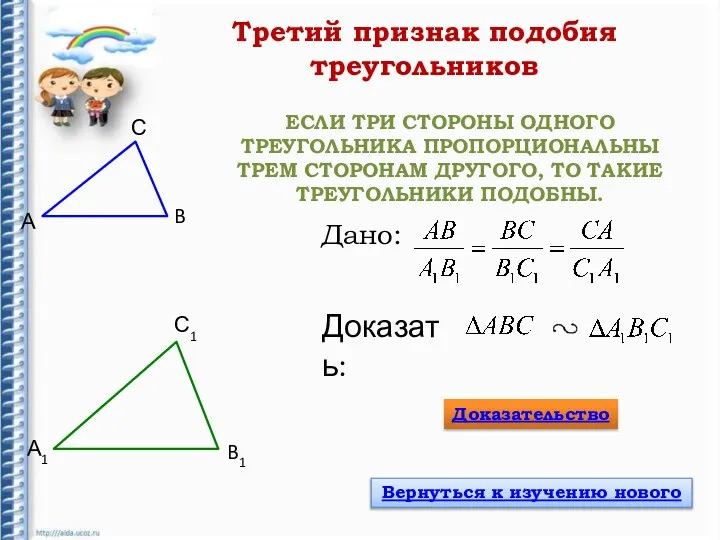
- 11. ЕСЛИ ТРИ СТОРОНЫ ОДНОГО ТРЕУГОЛЬНИКА ПРОПОРЦИОНАЛЬНЫ ТРЕМ СТОРОНАМ ДРУГОГО, ТО ТАКИЕ ТРЕУГОЛЬНИКИ ПОДОБНЫ. А B А1
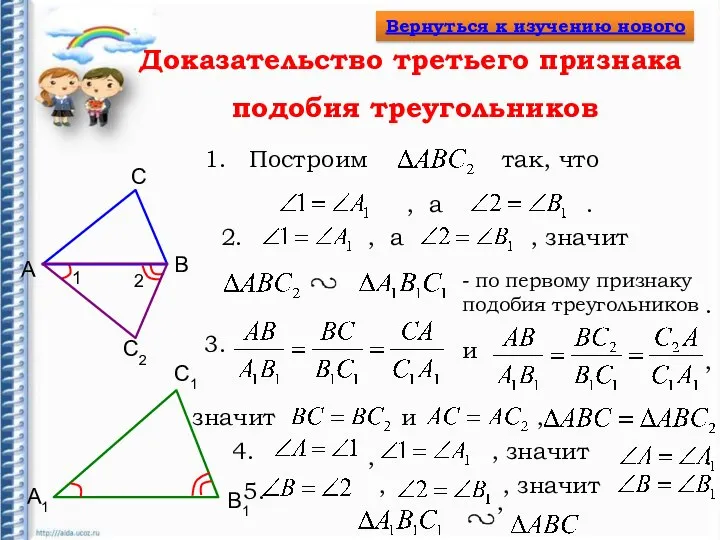
- 12. Доказательство третьего признака подобия треугольников А B А1 B1 С С1 С2 1 2 - по
- 13. Развиваем умения
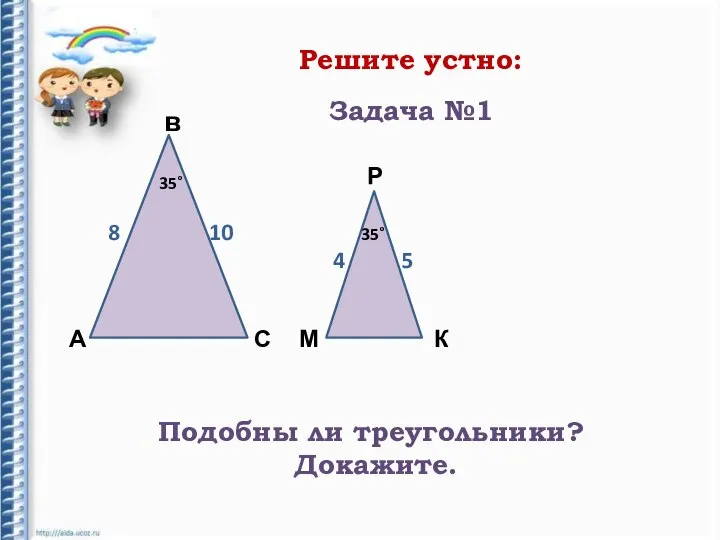
- 14. Решите устно: А в С Р К М 8 35˚ 35˚ 10 4 5 Подобны ли
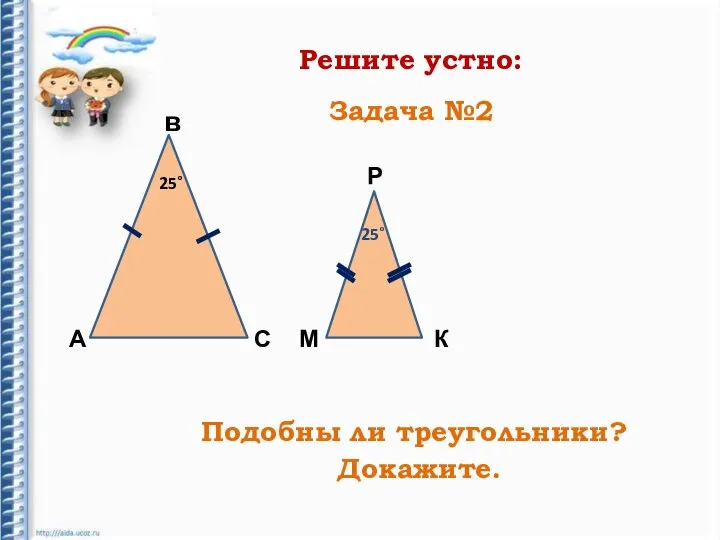
- 15. Решите устно: А в С Р К М 25˚ 25˚ Подобны ли треугольники? Докажите. Задача №2
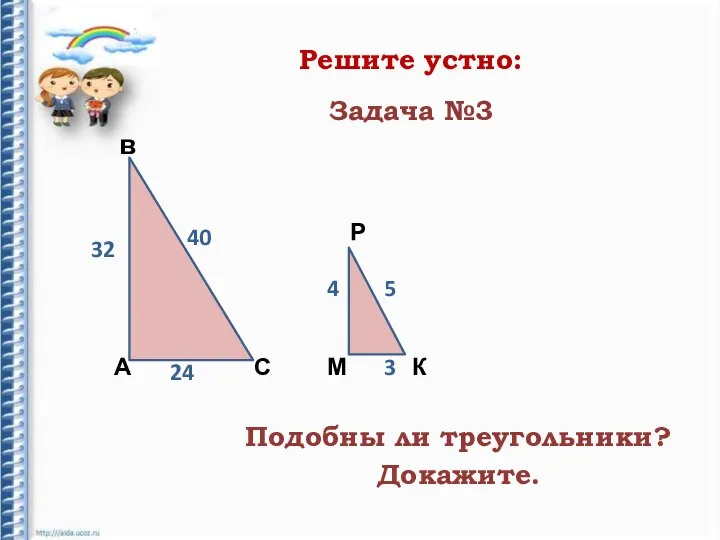
- 16. Решите устно: А в С Р К М 32 40 4 5 Подобны ли треугольники? Докажите.
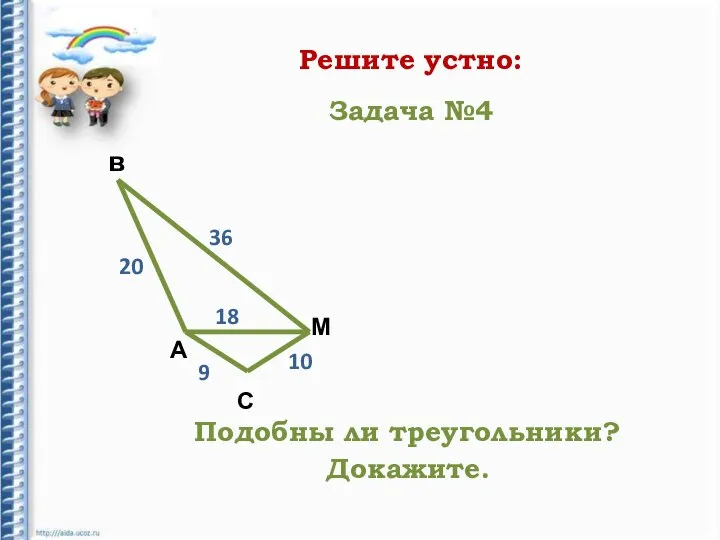
- 17. Решите устно: А в С М 20 36 10 Подобны ли треугольники? Докажите. Задача №4 18
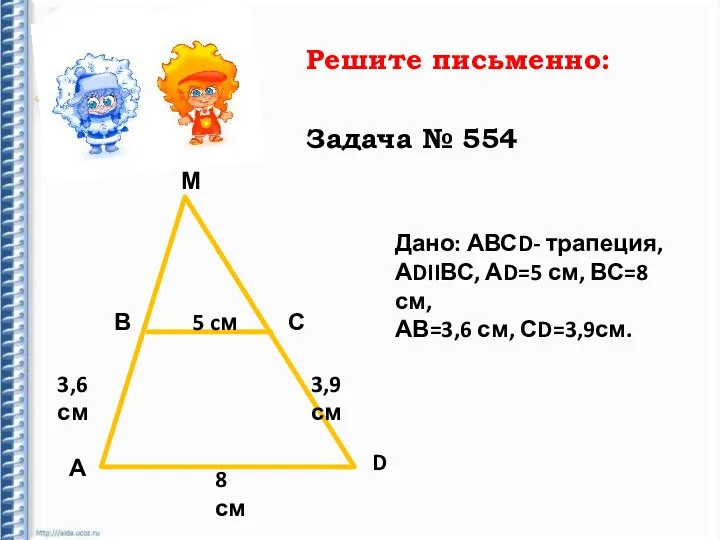
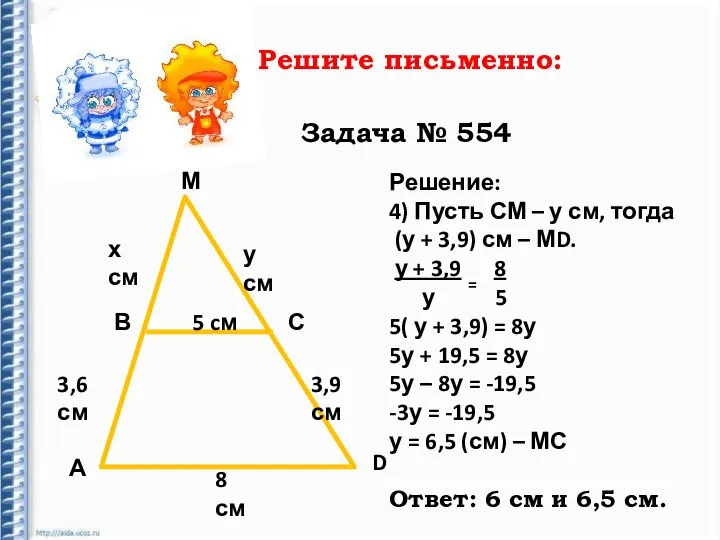
- 18. Решите письменно: Задача № 554
- 19. Решите письменно: Задача № 554 М В С А D 5 cм 3,6 см 3,9 см
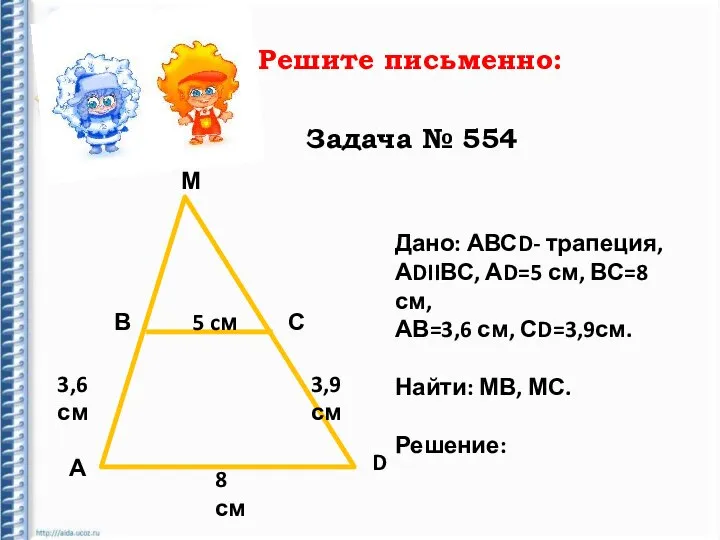
- 20. Решите письменно: Задача № 554 М В С А D 5 cм 3,6 см 3,9 см
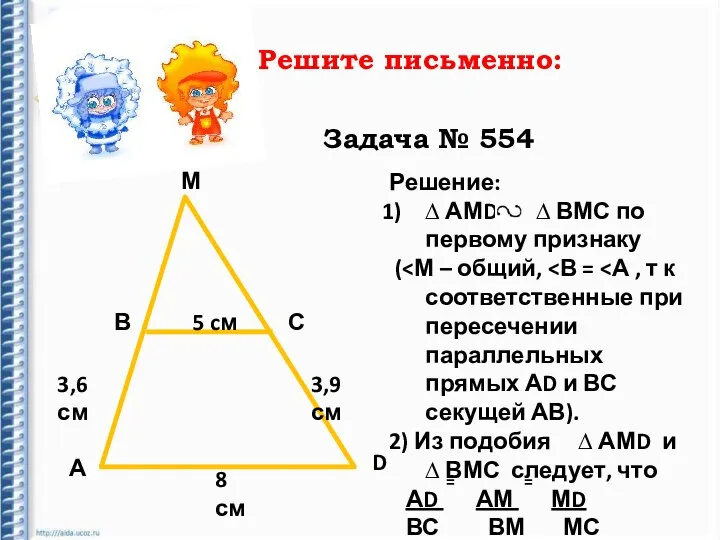
- 21. Решите письменно: Задача № 554 М В С А D 5 cм 3,6 см 3,9 см
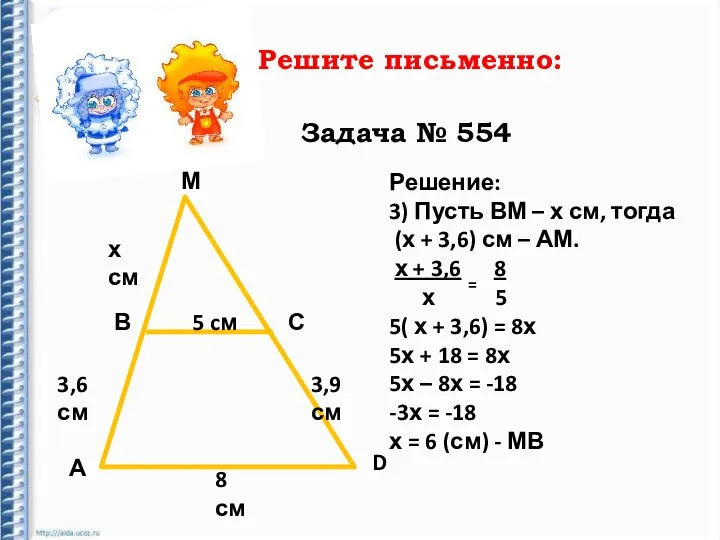
- 22. Решите письменно: Задача № 554 М В С А D 5 cм 3,6 см 3,9 см
- 23. Решите письменно: Задача № 554 М В С А D 5 cм 3,6 см 3,9 см
- 24. Домашнее задание: П. 57 – 61 формулировки наизусть № 550 № 555 (а) № 560 (а)
- 25. Вопросы к уроку: Какие треугольники называются подобными? Чему равно отношение площадей подобных треугольников? Сформулируйте признаки подобия
- 27. Скачать презентацию







 Векторы на плоскости
Векторы на плоскости Algorytmy i struktury danych
Algorytmy i struktury danych Деление на двузначное число
Деление на двузначное число Признаки параллелограмма. 8 класс
Признаки параллелограмма. 8 класс Решение треугольников
Решение треугольников Сложение, вычитание смешанных чисел. Задание для устного счета
Сложение, вычитание смешанных чисел. Задание для устного счета Расстояние от точки до прямой. Решение задач
Расстояние от точки до прямой. Решение задач Методика обучения решению простых задач
Методика обучения решению простых задач Дифференцирование. Производная функции в точке
Дифференцирование. Производная функции в точке Понятие теории игр
Понятие теории игр Правила нахождения производных
Правила нахождения производных Числовые промежутки
Числовые промежутки Полимино
Полимино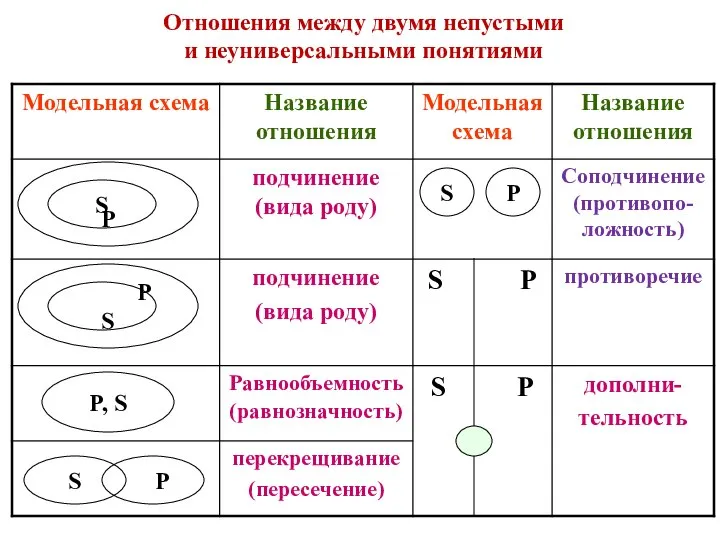 Отношения между двумя непустыми и неуниверсальными понятиями. Модельная схема
Отношения между двумя непустыми и неуниверсальными понятиями. Модельная схема Математика (1 класс)
Математика (1 класс) Теорема Муавра -Лапласа
Теорема Муавра -Лапласа Сложение и вычитание многозначных чисел
Сложение и вычитание многозначных чисел Практико-ориентированные задачи по математике про шины
Практико-ориентированные задачи по математике про шины Проектная деятельность в школе как показатель сформированности познавательных УУД
Проектная деятельность в школе как показатель сформированности познавательных УУД SLUChAJNYE_VELIChINY
SLUChAJNYE_VELIChINY В мире магических чисел
В мире магических чисел Понятие многогранник, призма
Понятие многогранник, призма Методы решения СЛДУ
Методы решения СЛДУ Правила построения алгоритма
Правила построения алгоритма Физический смысл производной
Физический смысл производной Движение
Движение Действия над десятичными дробями
Действия над десятичными дробями Углы, связанные с окружностью
Углы, связанные с окружностью