- Главная
- Информатика
- Кодирование и декодирование информации

Содержание
- 2. Задача 1. ИНФОРМАТИКА 2014г. Кирсанов Илья Андреевич © Для кодирования некоторой последовательности, состоящей из букв А,
- 3. В секундах. Задача 1. ИНФОРМАТИКА 2014г. Кирсанов Илья Андреевич © Решение. Мы видим, что выполняется условие
- 4. Рассмотрим варианты ответов. 1) ОК. Разбивать на части нужно так: 11 и 2. Возможные исходные 618
- 5. В секундах. Задача 2. ИНФОРМАТИКА 2014г. Кирсанов Илья Андреевич © Решение. Выберем коды, для которых выполнено
- 6. Рассмотрим варианты ответов. 1) ОК. Разбивать на части нужно так: 11 и 2. Возможные исходные 618
- 7. В секундах. Задача 3. ИНФОРМАТИКА 2014г. Кирсанов Илья Андреевич © Решение. Сначала следует представить данные в
- 8. Рассмотрим варианты ответов. 1) ОК. Разбивать на части нужно так: 11 и 2. Возможные исходные 618
- 9. В секундах. Задача 4. ИНФОРМАТИКА 2014г. Кирсанов Илья Андреевич © Решение. Закодируем каждое слово. КАА —
- 10. Вопросы. ИНФОРМАТИКА 2014г. Кирсанов Илья Андреевич © По каналу связи передаются сообщения, содержащие только 4 буквы:
- 11. Вопросы. ИНФОРМАТИКА 2014г. Кирсанов Илья Андреевич © По каналу связи передаются сообщения, содержащие только 4 буквы:
- 12. Вопросы. ИНФОРМАТИКА 2014г. Кирсанов Илья Андреевич © Для кодирования букв И, Д, Т, О, X решили
- 14. Скачать презентацию
Слайд 2Задача 1.
ИНФОРМАТИКА
2014г. Кирсанов Илья Андреевич ©
Для кодирования некоторой последовательности, состоящей из букв
Задача 1.
ИНФОРМАТИКА
2014г. Кирсанов Илья Андреевич ©
Для кодирования некоторой последовательности, состоящей из букв

Можно ли сократить для одной из букв длину кодового слова так, чтобы код по-прежнему можно было декодировать однозначно? Коды остальных букв меняться не должны. Выберите правильный вариант ответа.
1) это невозможно
2) для буквы В – 000
3) для буквы Б – 0
4) для буквы Г – 11
Слайд 3В секундах.
Задача 1.
ИНФОРМАТИКА
2014г. Кирсанов Илья Андреевич ©
Решение.
Мы видим, что выполняется условие
В секундах.
Задача 1.
ИНФОРМАТИКА
2014г. Кирсанов Илья Андреевич ©
Решение.
Мы видим, что выполняется условие

Чтобы сократить код одной буквы, необходимо выполнение условия Фано в новом коде.
Вариант 1 оставляем, пока не проверим остальные.
Вариант 2 подходит, так как не нарушает условия Фано.
Вариант 3 не подходит, потому что 0 является началом кода 0001.
Вариант 4 не подходит, потому что код 11 является началом кода 111.
Правильный ответ указан под номером 2.
Ответ 2
Слайд 4Рассмотрим варианты ответов.
1) ОК. Разбивать на части нужно так: 11 и
Рассмотрим варианты ответов.
1) ОК. Разбивать на части нужно так: 11 и

2) Не подходит. Разбить на части можно только так: 21 и 11. Число 218 нельзя получить, как сумму однозначных восьмеричных чисел. (нарушено условие в2).
3) Не подходит. Цифра 9 не может встречаться в восьмеричном числе.
4) Не подходит. Разбить на части можно только так: 2 и 7. При этом 2 > 7 (нарушено условие в3 - первое число должно быть больше второго)
Правильный ответ: 1
Задача 2.
ИНФОРМАТИКА
2014г. Кирсанов Илья Андреевич ©
По каналу связи передаются сообщения, содержащие только 4 буквы:
А, И, С, Т.
В любом сообщении больше всего букв А, следующая по частоте буква — С, затем — И. Буква Т встречается реже, чем любая другая.
Для передачи сообщений нужно использовать неравномерный двоичный код, допускающий однозначное декодирование; при этом сообщения должны быть как можно короче. Шифровальщик может использовать один из перечисленных ниже кодов. Какой код ему следует выбрать?
1) А−0, И−1, С−00, Т−11
2) С−1, И−0, А−01, Т−10
3) А−1, И−01, С−001, Т−000
4) С−0, И−11, А−101, Т−100
Слайд 5В секундах.
Задача 2.
ИНФОРМАТИКА
2014г. Кирсанов Илья Андреевич ©
Решение.
Выберем коды, для которых выполнено
В секундах.
Задача 2.
ИНФОРМАТИКА
2014г. Кирсанов Илья Андреевич ©
Решение.
Выберем коды, для которых выполнено

Следовательно, ответ 3, поскольку буква А — самая часто встречающаяся буква и для ее кодирования в варианте 3 используется один символ.
Ответ 3
Слайд 6Рассмотрим варианты ответов.
1) ОК. Разбивать на части нужно так: 11 и
Рассмотрим варианты ответов.
1) ОК. Разбивать на части нужно так: 11 и

2) Не подходит. Разбить на части можно только так: 21 и 11. Число 218 нельзя получить, как сумму однозначных восьмеричных чисел. (нарушено условие в2).
3) Не подходит. Цифра 9 не может встречаться в восьмеричном числе.
4) Не подходит. Разбить на части можно только так: 2 и 7. При этом 2 > 7 (нарушено условие в3 - первое число должно быть больше второго)
Правильный ответ: 1
Задача 3.
ИНФОРМАТИКА
2014г. Кирсанов Илья Андреевич ©
Для кодирования букв О, В, Д, П, А решили использовать двоичное представление чисел 0, 1, 2, 3 и 4 соответственно (с сохранением одного незначащего нуля в случае одноразрядного представления). Если закодировать последовательность букв ВОДОПАД таким способом и результат записать восьмеричным кодом, то получится
1) 22162
2) 1020342
3) 2131453
4) 34017
Слайд 7В секундах.
Задача 3.
ИНФОРМАТИКА
2014г. Кирсанов Илья Андреевич ©
Решение.
Сначала следует представить данные в
В секундах.
Задача 3.
ИНФОРМАТИКА
2014г. Кирсанов Илья Андреевич ©
Решение.
Сначала следует представить данные в

Затем закодировать последовательность букв:
ВОДОПАД — 01-00-10-00-11-100-10.
Теперь разобьём это представление на тройки справа налево и переведём полученный набор чисел в десятичный код, затем в восьмеричный (восьмеричное представление совпадает с десятичным при разбиении тройками, воспользуемся таблицей из А1)
010-010-001-110-010 — 22162.
Правильный ответ указан под номером 1.
Ответ 1
«сохранение одного незначащего нуля в случае одноразрядного представления»
Слайд 8Рассмотрим варианты ответов.
1) ОК. Разбивать на части нужно так: 11 и
Рассмотрим варианты ответов.
1) ОК. Разбивать на части нужно так: 11 и

2) Не подходит. Разбить на части можно только так: 21 и 11. Число 218 нельзя получить, как сумму однозначных восьмеричных чисел. (нарушено условие в2).
3) Не подходит. Цифра 9 не может встречаться в восьмеричном числе.
4) Не подходит. Разбить на части можно только так: 2 и 7. При этом 2 > 7 (нарушено условие в3 - первое число должно быть больше второго)
Правильный ответ: 1
Задача 4.
ИНФОРМАТИКА
2014г. Кирсанов Илья Андреевич ©
По каналу связи передаются сообщения, содержащие только 5 букв А, И, К, О, Т. Для кодирования букв используется неравномерный двоичный код с такими кодовыми словами:
А — 0, И — 00, К — 10, О — 110, Т — 111.
Среди приведённых ниже слов укажите такое, код которого можно декодировать только одним способом. Если таких слов несколько, укажите первое по алфавиту.
1) КАА
2) ИКОТА
3) КОТ
4) ни одно из сообщений не подходит
Слайд 9В секундах.
Задача 4.
ИНФОРМАТИКА
2014г. Кирсанов Илья Андреевич ©
Решение.
Закодируем каждое слово.
КАА — 1000
ИКОТА
В секундах.
Задача 4.
ИНФОРМАТИКА
2014г. Кирсанов Илья Андреевич ©
Решение.
Закодируем каждое слово.
КАА — 1000
ИКОТА

КОТ — 10110111
Слово КАА можно декодировать как КИ
Слово ИКОТА можно декодировать как ААКОТА
Слово КОТ никак нельзя декодировать по-другому.
Следовательно, ответ 3.
Ответ 3
Слайд 10Вопросы.
ИНФОРМАТИКА
2014г. Кирсанов Илья Андреевич ©
По каналу связи передаются сообщения, содержащие только 4
Вопросы.
ИНФОРМАТИКА
2014г. Кирсанов Илья Андреевич ©
По каналу связи передаются сообщения, содержащие только 4

Для этого набора кодовых слов выполнено такое свойство: любые два слова из набора отличаются не менее чем в трех позициях.
Это свойство важно для расшифровки сообщений при наличии помех. Какое из перечисленных ниже кодовых слов можно использовать для буквы T, чтобы указанное свойство выполнялось для всех четырёх кодовых слов?
1) 00000
2) 11100
3) 00011
4) не подходит ни одно из указанных слов
Ответ 3
Слайд 11Вопросы.
ИНФОРМАТИКА
2014г. Кирсанов Илья Андреевич ©
По каналу связи передаются сообщения, содержащие только 4
Вопросы.
ИНФОРМАТИКА
2014г. Кирсанов Илья Андреевич ©
По каналу связи передаются сообщения, содержащие только 4

1) 1
2) 0
3) 01
4) 101
Ответ 3
Слайд 12Вопросы.
ИНФОРМАТИКА
2014г. Кирсанов Илья Андреевич ©
Для кодирования букв И, Д, Т, О, X
Вопросы.
ИНФОРМАТИКА
2014г. Кирсанов Илья Андреевич ©
Для кодирования букв И, Д, Т, О, X

1) CD89
2) 89CD
3) 3154542
4) 2043431
Ответ 2
 Язык HTML. Оформление текста
Язык HTML. Оформление текста Тестирование, верификация и валидация ПО
Тестирование, верификация и валидация ПО Циклы с неизвестным числом повторений, итерационные
Циклы с неизвестным числом повторений, итерационные Разработка электронного бизнес-консультанта
Разработка электронного бизнес-консультанта Domaine. Concise reference sheets v2.0 by hecose
Domaine. Concise reference sheets v2.0 by hecose Вечеринка ситхов – лучшая группа в Вк
Вечеринка ситхов – лучшая группа в Вк Поиск записей в табличной базе данных с помощью фильтров
Поиск записей в табличной базе данных с помощью фильтров Что такое учебный проект?
Что такое учебный проект? Логические основы компьютеров
Логические основы компьютеров Жанр и метод интервью
Жанр и метод интервью 10u-2b_СистемыСчисления
10u-2b_СистемыСчисления Системы счисления
Системы счисления Язык программирования Pascal Повторение А. Жидков
Язык программирования Pascal Повторение А. Жидков Преобразование информации по заданным правилам
Преобразование информации по заданным правилам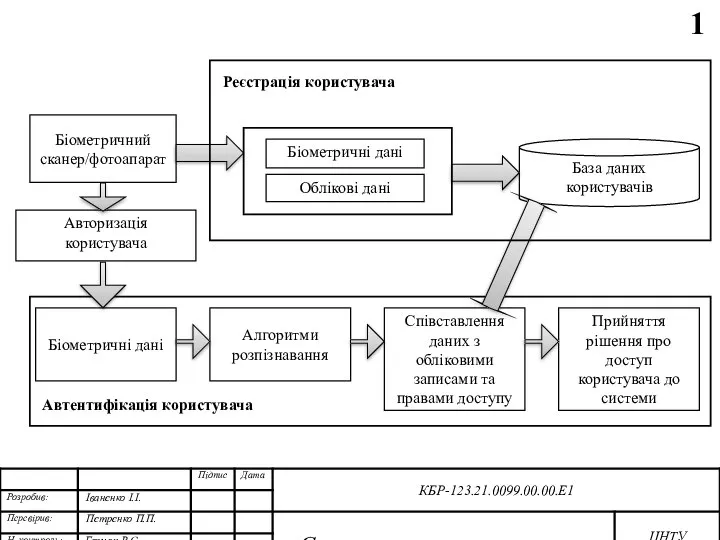 Приклад презентації. Реєстрація користувача
Приклад презентації. Реєстрація користувача Рамки для аватарок
Рамки для аватарок Типы данных языка С++, основные логические операторы языка
Типы данных языка С++, основные логические операторы языка Разработка баз данных
Разработка баз данных Web-сервис для отдела по приему автомобилей предприятия Автотрейд
Web-сервис для отдела по приему автомобилей предприятия Автотрейд Tinder - твой золотой поток успеха
Tinder - твой золотой поток успеха Рабочий стол
Рабочий стол Главный вычислительный центр – филиал ОАО РЖД
Главный вычислительный центр – филиал ОАО РЖД Умозаключение (4 класс)
Умозаключение (4 класс) Основные цели автоматизированного проектирования
Основные цели автоматизированного проектирования Разработка системы распознавания печатного текста
Разработка системы распознавания печатного текста Учебник Паскаль
Учебник Паскаль Cyber Motion 3D-Designer. Основные действия и рабочее поле
Cyber Motion 3D-Designer. Основные действия и рабочее поле UA-IX Проблемы внедрения протокола IPv6 в Украине
UA-IX Проблемы внедрения протокола IPv6 в Украине