- Главная
- Информатика
- Функциональное описание и моделирование систем

Содержание
- 2. Функциональная организация может быть описана: алгоритмически, аналитически, графически, таблично, посредством временных диаграмм функционирования, вербально (словесно). Описание
- 3. В самом общем виде функциональное описание системы в любой динамической системе изображается семеркой: Sf={T, x, C,
- 4. Рациональный путь формирования функционального описания состоит в применении такой многоуровневой иерархии описаний, при которой описание более
- 5. Путем построения иерархии (параметры b-го уровня - процессы (b-1)-го уровня - параметры (b-1)-го уровня) можно связать
- 6. ГРАФИЧЕСКИЕ СПОСОБЫ ФУНКЦИОНАЛЬНОГО ОПИСАНИЯ СИСТЕМ Выше был рассмотрен способ обобщенного аналитического функционального описания систем. Очень часто
- 7. Дерево функций системы представляет декомпозицию функций системы и формируется с целью детального исследования функциональных возможностей системы
- 8. Моделирование сложных систем (какими являются современные промышленные системы) было начато в программе интегрированной автоматизации производства (ICAM
- 9. При этом каждая из функций конкретно взятого i-ого уровня может рассматриваться как макрофункция по отношению к
- 10. Объектами моделирования являются системы. Описание IDEF0 модели построено в виде иерархической пирамиды, в вершине которой представляется
- 11. Диаграммы должны иметь связанный интерфейс, когда номера Блоков, Дуги и ICOM коды имеют единую структуру. Уникальность
- 12. В рамках методологии IDEF0 модель системы описывается при помощи Графических IDEF0 Диаграмм и уточняется за счет
- 13. Хотя вершиной модели является Диаграмма уровня А-0, настоящей “рабочей вершиной или структурой” является Диаграмма А0, поскольку
- 14. Управляющие выполнением функции данные входят в блок сверху, в то время как информация, которая подвергается воздействию
- 15. ДУГИ, КАК ОГРАНИЧИВАЮЩИЕ И УТОЧНЯЮЩИЕ ФАКТОРЫ БЛОКА
- 16. ПРИМЕР А0 ДИАГРАММЫ
- 17. Функциональные Блоки на Диаграмме изображаются в виде прямоугольников, внутри которых записывается имя функции и номер Блок
- 18. – Взаимосвязь по управлению, – когда выход одного Блока влияет (является управляющей) на выполнение функции в
- 19. – Обратная связь по входу, – когда выход из одной функции является входом для другой функции,
- 20. Пример. Рассмотрим немного надуманный пример системы – некоторый отдел контроля, созданный для оценки эффективности управления и
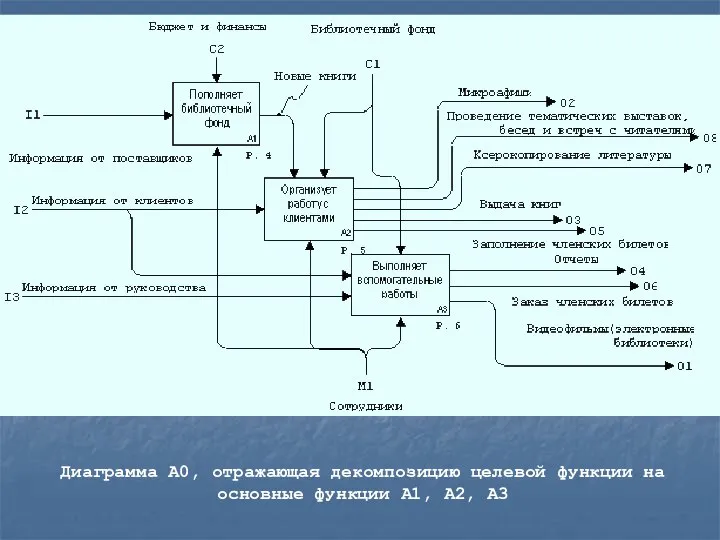
- 21. Диаграмма А0, отражающая декомпозицию целевой функции на основные функции А1, А2, А3
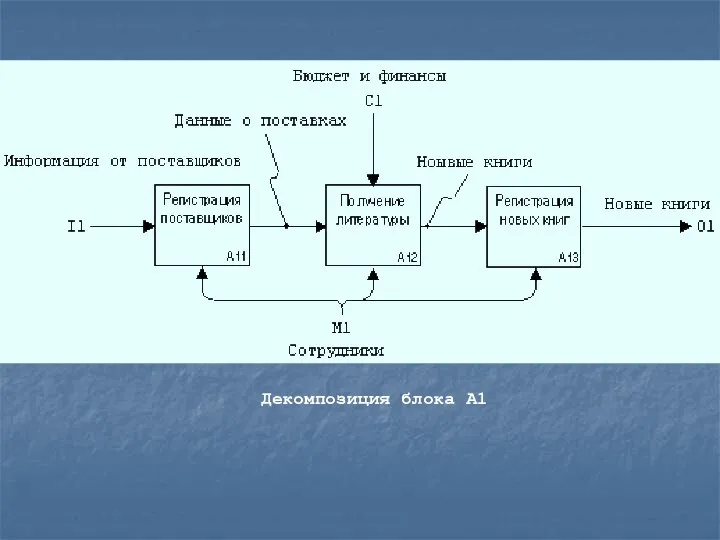
- 22. Декомпозиция блока А1
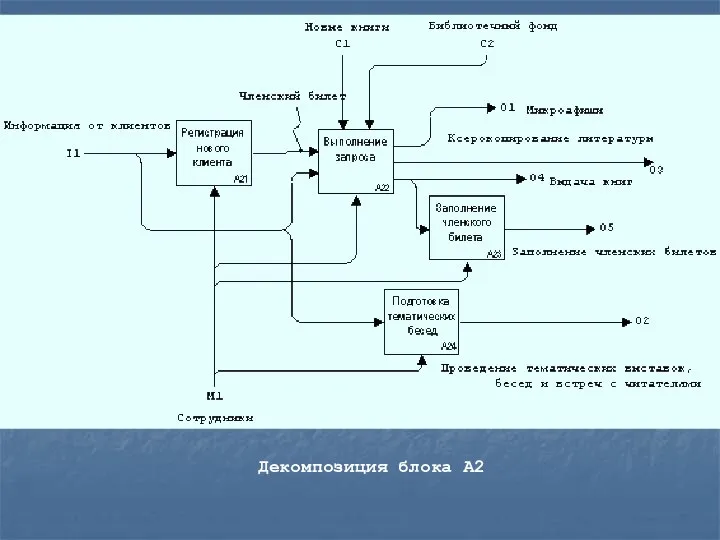
- 23. Декомпозиция блока А2
- 25. Скачать презентацию
Слайд 2 Функциональная организация может быть описана:
алгоритмически,
аналитически,
графически,
таблично,
посредством временных
Функциональная организация может быть описана:
алгоритмически,
аналитически,
графически,
таблично,
посредством временных

вербально (словесно).
Описание должно соответствовать концепции развития систем определенного класса и удовлетворять некоторым требованиям:
должно быть открытым и допускать возможность расширения (сужения) спектра функций, реализуемых системой;
предусматривать возможность перехода от одного уровня рассмотрения к другому, т.е. обеспечивать построение виртуальных моделей систем любого уровня.
При описании системы будем рассматривать ее как структуру, в которую в определенные моменты времени вводится нечто (вещество, энергия, информация), и из которой в определенные моменты времени нечто выводится.
Слайд 3 В самом общем виде функциональное описание системы в любой динамической системе
В самом общем виде функциональное описание системы в любой динамической системе

Sf={T, x, C, Q, y, φ, η},
где T - множество моментов времени,
х - множество мгновенных значений входных воздействий,
С = {c: T→x} – множество допустимых входных воздействий;
Q – множество состояний;
y - множество значений выходных величин;
Y={u:T→y} - множество выходных величин;
φ = {T×T×T×c→Q} - переходная функция состояния;
η: T×Q→y – выходное отображение;
с - отрезок входного воздействия;
u – отрезок выходной величины.
Такое описание системы охватывает широкий диапазон свойств.
Недостаток данного описания – не конструктивность: трудность интерпретации и практического применения. Функциональное описание должно отражать такие характеристики сложных и слабо познанных систем как параметры, процессы, иерархию.
Примем, что система S выполняет N функций ψ1, ψ2, …,ψs, …,ψN, зависящих от n процессов F1, F2, …,Fi, …, Fn. Эффективность выполнения s-й функции Эs = Эs(ψs) =Э(F1, F2, …,Fi, …, Fn) =Эs({Fi}), i=1…n, s=1…N.
Общая эффективность системы есть вектор-функционал Э={Эs}. Эффективность системы зависит от огромного количества внутренних и внешних факторов.
Слайд 4 Рациональный путь формирования функционального описания состоит в применении такой многоуровневой иерархии
Рациональный путь формирования функционального описания состоит в применении такой многоуровневой иерархии

Иерархия создается по уровневой факторизацией процессов { Fi } при помощи обобщенных параметров { Qi }, являющихся функционалами { Fi }. Предполагается, что число параметров значительно меньше числа переменных, от которых зависят процессы. Такой способ описания позволяет построить мост между свойствами взаимодействующих со средой элементов (подсистемами низшего уровня) и эффективностью системы.
Процессы { Fi(1) } можно обнаружить на выходе системы. Это процессы взаимодействия со средой. Будем называть их процессами первого уровня и полагать, что они определяются:
a) параметрами системы первого уровня - Q1(1), Q2(1),…, Qj(1),…, Qm(1) ;
б) активными противодействующими параметрами среды, непосредственно направленными против системы для снижения ее эффективности - b1, b2,…, bk,…, bК;
в) нейтральными (случайными параметрами среды) c1, c2,…, cl,…, cL;
г) благоприятными параметрами среды d1, d2,…, dp,…, dP.
Среда имеет непосредственный контакт с подсистемами низших уровней, воздействуя через них на подсистемы более высокого уровня иерархии, так что Fi*= Fi*({bk},{cl}, {dp}).
Слайд 5 Путем построения иерархии (параметры b-го уровня - процессы (b-1)-го уровня -
Путем построения иерархии (параметры b-го уровня - процессы (b-1)-го уровня -

Собственным функциональным пространством системы W называется пространство, точками которого являются все возможные состояния системы, определяемое множеством параметров до уровня b:
Q={Q(1), Q(2), …Q(b) }. Состояние может сохраняться постоянным на некотором интервале времени Т. Процессы {Fi(2)} не могут быть обнаружены на выходе системы. Это процессы второго уровня, зависящие от параметров Q(2) подсистем системы (параметров второго уровня). И так далее.
Образуется иерархия описания: эффективность (конечное множество функционалов) – процессы первого уровня (функции) – параметры первого уровня (функционалы) - процессы второго уровня (функции) – параметры второго уровня (функционалы) и т.д. На каком-то уровне наши знания о функциональных свойствах системы исчерпываются, и иерархия обрывается. Обрыв может произойти на разном уровне для разных параметров (процессов), причем как на процессе, так и на параметре. Внешние характеристики системы определяются верхним уровнем иерархии, поэтому часто удается ограничиться описанием вида ({Эi},{ψS}, {Fi(1)}, {Qj(1)}, {bk}, {cl}, {dp}). Число уровней иерархии зависит от требуемой точности представления входных процессов.
Слайд 6ГРАФИЧЕСКИЕ СПОСОБЫ ФУНКЦИОНАЛЬНОГО ОПИСАНИЯ СИСТЕМ
Выше был рассмотрен способ обобщенного аналитического функционального
ГРАФИЧЕСКИЕ СПОСОБЫ ФУНКЦИОНАЛЬНОГО ОПИСАНИЯ СИСТЕМ
Выше был рассмотрен способ обобщенного аналитического функционального

Все функции, реализуемые сложной системой, могут быть условно разделены на три группы:
целевая функция;
базисные функции системы;
дополнительные функции системы.
Целевая функция системы соответствует ее основному функциональному назначению, т.е. целевая (главная) функция – отражает назначение, сущность и смысл существования системы.
Основные функции отражают ориентацию системы и представляют собой совокупность макрофункций, реализуемых системой. Эти функции обусловливают существование системы определенного класса. Основные функции – обеспечивают условия выполнения целевой функции (прием, передача приобретение, хранение, выдача).
Дополнительные (сервисные) функции расширяют функциональные возможности системы, сферу их применения и способствуют улучшению показателей качества системы. Дополнительные функции – обеспечивают условия выполнения основных функций (соединение (разведение, направление, гарантирование)).
Слайд 7 Дерево функций системы представляет декомпозицию функций системы и формируется с целью
Дерево функций системы представляет декомпозицию функций системы и формируется с целью

Исходными данными для формирования дерева функций являются основные и дополнительные функции системы. Формирование дерева функций представляет процесс декомпозиции целевой функции и множества основных и дополнительных функций на более элементарные функции, реализуемые на последующих уровнях декомпозиции. При этом каждая из функций конкретно взятого i-ого уровня может рассматриваться как макрофункция по отношению к реализующим ее функциям на (i+1)-го уровня, и как элементарная функция по отношению к соответствующей функции верхнего (i-1)-го уровня.
Слайд 8Моделирование сложных систем (какими являются современные промышленные системы) было начато в программе
Моделирование сложных систем (какими являются современные промышленные системы) было начато в программе

Слайд 9 При этом каждая из функций конкретно взятого i-ого уровня может рассматриваться
При этом каждая из функций конкретно взятого i-ого уровня может рассматриваться

КРАТКОЕ ОПИСАНИЕ МЕТОДОЛОГИИ IDEF0
Моделирование сложных систем (какими являются современные промышленные системы) было начато в программе интегрированной автоматизации производства (ICAM - (Integrated Computer Aided Manufacturing) Министерства обороны США в которой была признана полезность методологии SADT (Structured Analysis and Design Technique - Технология структурного анализа и проектирования) введенной в 1973 году Россом, что привело к стандартизации и публикации ее части, называемой IDEF0 (IDEF=ICAM DEFinition или Integration Definition for Function Modeling). C 1981 года стандарт IDEF0 претерпел несколько незначительных изменений, в основном ограничивающего характера, и последняя его редакция была выпущена в декабре 1993 года Национальным Институтом по Стандартам и Технологиям США (NIST). В 2000 году – IDEF0 был принят в качестве стандарта в Российской Федерации.
Слайд 10Объектами моделирования являются системы.
Описание IDEF0 модели построено в виде иерархической
Объектами моделирования являются системы.
Описание IDEF0 модели построено в виде иерархической

IDEF0 методология построена на следующих принципах:
Графическое описание моделируемых процессов. Графический язык Блоков и Дуг IDEF0 Диаграмм отображает операции или функции в виде Блоков, а взаимодействие между входами/выходами операций, входящими в Блок или выходящими из него, Дугами.
Лаконичность. За счет использования графического языка описания процессов достигается с одной стороны точность описания, а с другой – краткость.
Необходимость соблюдения правил и точность передачи информации. При IDEF0 моделировании необходимо придерживаться следующих правил:
На Диаграмме должно быть не менее 3-х и не более 6-и функциональных Блоков.
Диаграммы должны отображать информацию, не выходящую за рамки контекста, определенного целью и точкой зрения.
Слайд 11 Диаграммы должны иметь связанный интерфейс, когда номера Блоков, Дуги и ICOM
Диаграммы должны иметь связанный интерфейс, когда номера Блоков, Дуги и ICOM

Уникальность имен функций Блоков и наименований Дуг.
Четкое определение роли данных и разделение входов и управлений.
Замечания для Дуг и имена функций Блоков должны быть краткими и лаконичными.
Для каждого функционального Блока необходима как минимум одна управляющая Дуга.
Модель всегда строится с определенной целью и с позиций конкретной точки зрения.
В процессе моделирования очень важным является четко определить направление разработки модели – ее контекст, точку зрения и цель.
Контекст модели очерчивает границы моделируемой системы и описывает ее взаимосвязи с внешней средой.
Точка зрения определяет позицию автора, т.е. что будет рассматриваться и под каким углом зрения.
Необходимо помнить, что одна модель представляет одну точку зрения. Для моделирования системы с нескольких точек зрения используется несколько моделей.
Цель отражает причину создания модели и определяет ее назначение. При этом, все взаимодействия в модели рассматриваются именно с точки зрения достижения поставленной цели.
Слайд 12 В рамках методологии IDEF0 модель системы описывается при помощи Графических IDEF0
В рамках методологии IDEF0 модель системы описывается при помощи Графических IDEF0

Разработка IDEF0 Диаграмм начинается с построения самого верхнего уровня иерархии (А-0) – одного Блока и интерфейсных Дуг, описывающих внешние связи рассматриваемой системы. Имя функции, записываемое в Блоке 0, является целевой функцией системы с принятой точки зрения и цели построения модели.
При дальнейшем моделировании Блок 0 декомпозируется на Диаграмме А0, где целевая функция уточняется с помощью нескольких Блоков, взаимодействие между которыми описывается с помощью Дуг. В свою очередь, функциональные Блоки на Диаграмме А0 могут быть также декомпозированы для более детального представления.
В результате, имена функциональных Блоков и интерфейсные Дуги, описывающие взаимодействие всех Блоков, представленных на Диаграммах, образуют иерархическую взаимосогласованную модель.
Слайд 13 Хотя вершиной модели является Диаграмма уровня А-0, настоящей “рабочей вершиной или
Хотя вершиной модели является Диаграмма уровня А-0, настоящей “рабочей вершиной или

ОПИСАНИЕ СИНТАКСИСА ЯЗЫКА МОДЕЛИРОВАНИЯ
Основными элементами на IDEF0 Диаграммах являются Блоки и Дуги.
Блоки служат для отображения функций (действий), выполняемых моделируемой системой. Сформулированные функции должны содержать глагольный оборот.
глагол + объект действия + [дополнение].
Например: обрабатывать деталь на станке, передать документы в отдел, разработать план-график проведения анализа, опубликовать материалы...
Дуги служат для отображения информации или материальных объектов, которые необходимы для выполнения функции или появляются в результате ее выполнения (объекты, обрабатываемые системой). Под объектами в рамках функционального моделирования могут пониматься документы, физические материалы, инструменты, станки, информация, организации и даже системы.
Место соединения дуги с блоком определяет тип интерфейса.
Слайд 14 Управляющие выполнением функции данные входят в блок сверху, в то время
Управляющие выполнением функции данные входят в блок сверху, в то время
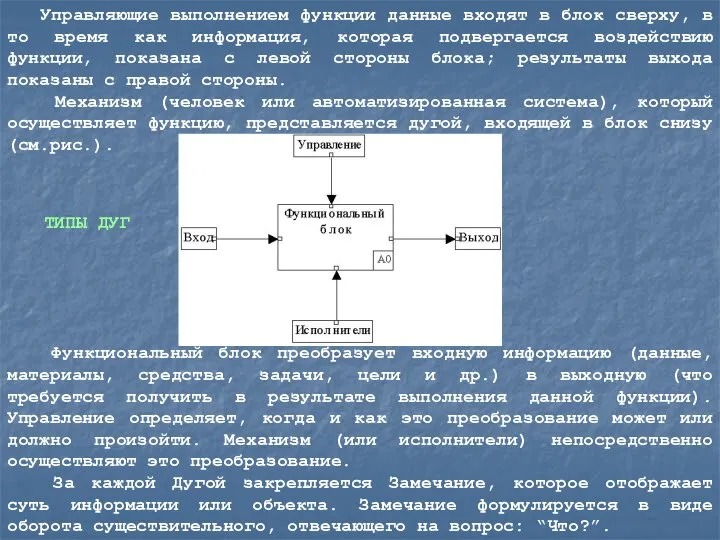
Механизм (человек или автоматизированная система), который осуществляет функцию, представляется дугой, входящей в блок снизу (см.рис.).
ТИПЫ ДУГ
Функциональный блок преобразует входную информацию (данные, материалы, средства, задачи, цели и др.) в выходную (что требуется получить в результате выполнения данной функции). Управление определяет, когда и как это преобразование может или должно произойти. Механизм (или исполнители) непосредственно осуществляют это преобразование.
За каждой Дугой закрепляется Замечание, которое отображает суть информации или объекта. Замечание формулируется в виде оборота существительного, отвечающего на вопрос: “Что?”.
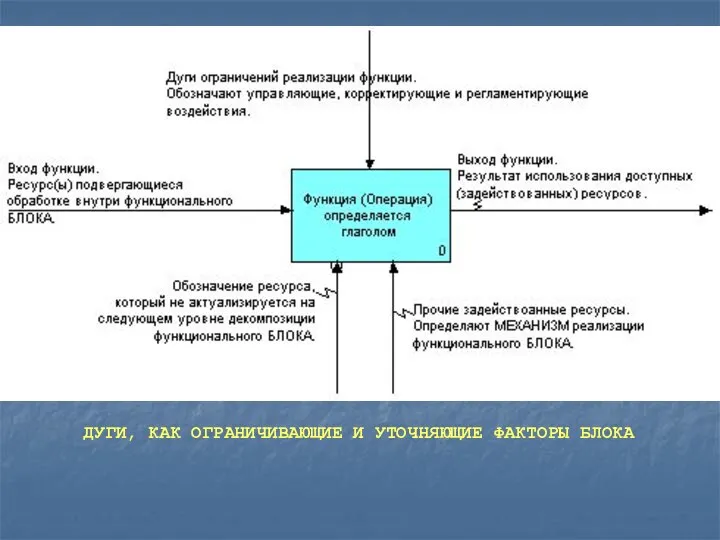
Слайд 15ДУГИ, КАК ОГРАНИЧИВАЮЩИЕ И УТОЧНЯЮЩИЕ ФАКТОРЫ БЛОКА
ДУГИ, КАК ОГРАНИЧИВАЮЩИЕ И УТОЧНЯЮЩИЕ ФАКТОРЫ БЛОКА
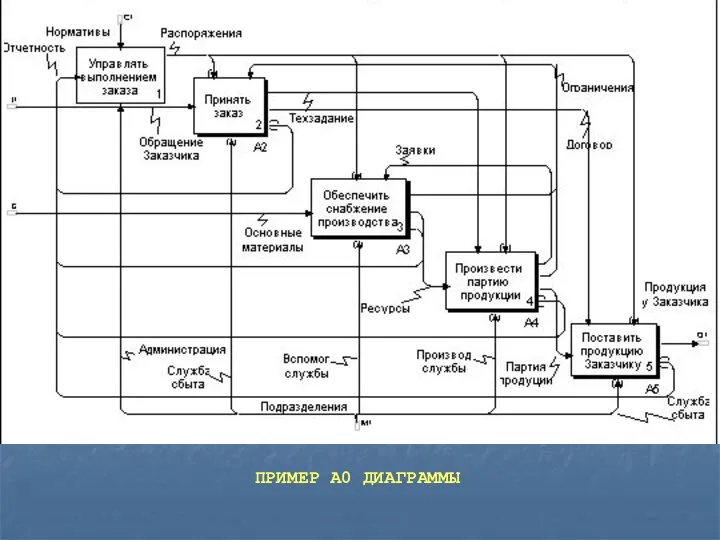
Слайд 16ПРИМЕР А0 ДИАГРАММЫ
ПРИМЕР А0 ДИАГРАММЫ
Слайд 17 Функциональные Блоки на Диаграмме изображаются в виде прямоугольников, внутри которых записывается
Функциональные Блоки на Диаграмме изображаются в виде прямоугольников, внутри которых записывается

Блоки располагаются на Диаграмме согласно их степени важности (по мнению автора модели). При этом доминирующим является тот Блок, выполнение функции которого оказывает влияние на выполнение всех остальных функций, представленных на Диаграмме. К примеру, это может быть Блок, содержащий контролирующую или планирующую функцию, выходы которого являются управляющими для всех остальных функциональных Блоков Диаграммы.
Доминирующий Блок помещается, как правило, в верхнем левом углу листа Диаграммы, а наименее важный Блок – в правом нижнем углу. Таким образом, ступенчатость Блоков на Диаграмме отражает мнение автора о доминировании одних Блоков относительно других.
Очень важно помнить, что доминирование блоков на диаграмме не задаёт чёткой временной зависимости операций.
Стороны Блока также имеют определенное значение. К левой границе Блока присоединяются входные Дуги, к верхней – управляющие Дуги, к правой – выходные Дуги, а к нижней – Дуги механизмов.
Дуги на IDEF0 Диаграмме изображаются в виде стрелок.
При IDEF0 моделировании используются пять типов взаимосвязей между Блоками, для описания их отношений.
Слайд 18– Взаимосвязь по управлению, – когда выход одного Блока влияет (является управляющей)
– Взаимосвязь по управлению, – когда выход одного Блока влияет (является управляющей)
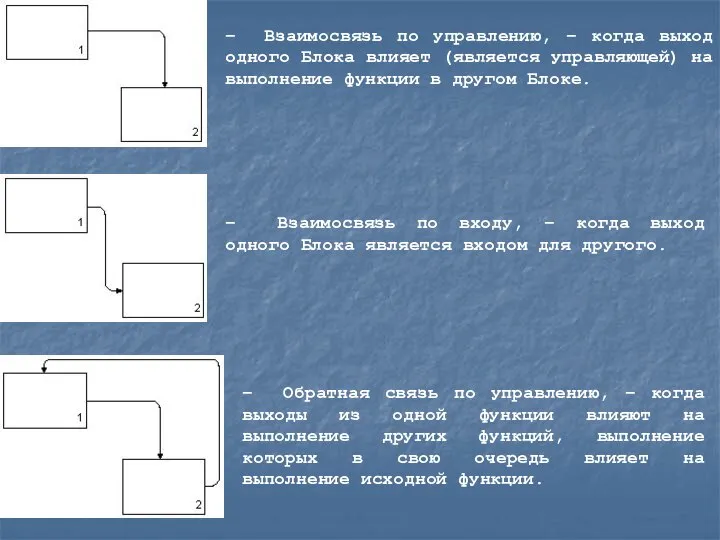
– Взаимосвязь по входу, – когда выход одного Блока является входом для другого.
– Обратная связь по управлению, – когда выходы из одной функции влияют на выполнение других функций, выполнение которых в свою очередь влияет на выполнение исходной функции.
Слайд 19– Обратная связь по входу, – когда выход из одной функции является
– Обратная связь по входу, – когда выход из одной функции является

– Взаимосвязь “выход-механизм”, – когда выход одной функции является механизмом для другой. Иначе говоря, выходная Дуга одного Блока является Дугой механизма для другого. Такой тип связи встречается редко и относится чаще всего к подготовительным операциям.
Поскольку содержание IDEF0 Диаграмм уточняется в ходе моделирования постепенно, Дуги на Диаграммах редко изображают один объект. Чаще всего они отображают определенный набор объектов и могут иметь множество начальных точек (источников) и определенное количество конечных точек (приемников). В ходе разработки графической Диаграммы для отражения этой особенности используют механизм разветвления/слияния Дуг. Это позволяет не только уточнить с использованием Замечаний содержание каждой ветви разветвленной Дуги (потока объектов), но и более точно описать из каких наборов объектов состоит входящая в функциональный Блок Дуга, если она получена путем слияния.
Слайд 20Пример.
Рассмотрим немного надуманный пример системы – некоторый отдел контроля, созданный для
Пример.
Рассмотрим немного надуманный пример системы – некоторый отдел контроля, созданный для
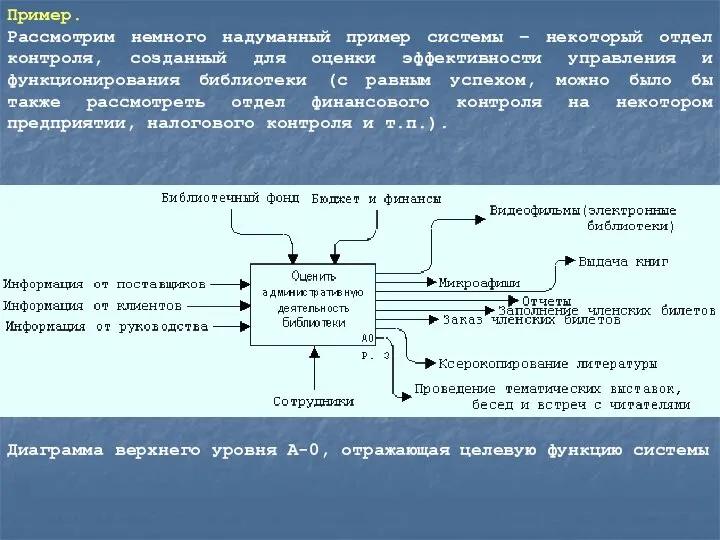
Диаграмма верхнего уровня А-0, отражающая целевую функцию системы
Слайд 22Декомпозиция блока А1
Декомпозиция блока А1
Слайд 23Декомпозиция блока А2
Декомпозиция блока А2
 Методические аспекты эволюции информационных технологий. NBICS-конвергенция
Методические аспекты эволюции информационных технологий. NBICS-конвергенция Компьютерная школа Инфосфера. Профессии компьютера
Компьютерная школа Инфосфера. Профессии компьютера Создание 3D объектов в Inkscape
Создание 3D объектов в Inkscape Программирование на языке Си. Введение
Программирование на языке Си. Введение Quiz in Java Script
Quiz in Java Script Исполнитель Калькулятор
Исполнитель Калькулятор Диаграммы взаимодействия Interaction diagrams
Диаграммы взаимодействия Interaction diagrams Логические основы устройства компьютера: базовые логические элементы
Логические основы устройства компьютера: базовые логические элементы Digital Paper. Цифровая бумага. Новый цифровой носитель информации
Digital Paper. Цифровая бумага. Новый цифровой носитель информации Instagram weekend. What did celebrities do yesterday
Instagram weekend. What did celebrities do yesterday История развития сети Интернет
История развития сети Интернет Компьютерная графика
Компьютерная графика Питание в школе. Школа будущего
Питание в школе. Школа будущего Дискретная форма представления информации. Единицы измерения информации
Дискретная форма представления информации. Единицы измерения информации Реквием по фронту. Библиотека Korolev
Реквием по фронту. Библиотека Korolev База данных. Типы моделей баз данных
База данных. Типы моделей баз данных О соцсетях. Александр Гуков
О соцсетях. Александр Гуков Использование ГИС-технологий для функционально-экологической оценки лесов
Использование ГИС-технологий для функционально-экологической оценки лесов Базовая обработка изображений
Базовая обработка изображений Урок 8 Создание графических изображений
Урок 8 Создание графических изображений Русские Instagram-маски. Команда вселенная
Русские Instagram-маски. Команда вселенная Презентация на тему Исполнитель Робот
Презентация на тему Исполнитель Робот  Презентация на тему Научно-технический прогресс
Презентация на тему Научно-технический прогресс  Лекция 1 (2) (1)
Лекция 1 (2) (1) Триггеры в презентации. Применение. Создание слайдов с триггерами
Триггеры в презентации. Применение. Создание слайдов с триггерами Загрузочные вирусы
Загрузочные вирусы Вопросы - программирование (8 класс)
Вопросы - программирование (8 класс) Представление информации в табличной форме
Представление информации в табличной форме