Кодирование источника (эффективное кодирование)

Кодирование источника
Для источников с памятью избыточность тем больше, чем выше степень статистической (вероятностной) зависимости символов в сообщении, при этом неопределенность относительно очередного символа в сообщении уменьшается, соответственно уменьшается и количество информации, переносимое этим символом.

Кодирование
Один символ источника → кодовое слово (кодовая комбинация)
Если для всех символов источника длина кодовых слов одинакова, код называют равномерным, в противном случае – неравномерным.
Примером равномерного кода является код Бодó:
каждая из букв алфавита представляется двоичным числом фиксированной разрядности (например, а → 00001, б → 00010 и т.д.). Тогда для алфавита из 32 символов достаточно 5-значного кода.
Jean-Maurice-Émile
Baudot, 1845 —1903

При неравномерном коде говорят о средней длине кодового слова (усреднение длин кодовых слов производится по априорному распределению вероятностей символов источника):

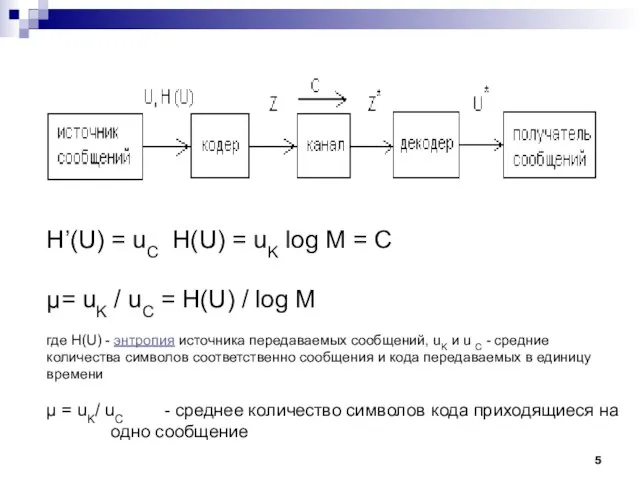
H’(U) = uC H(U) = uK log M = C
µ= uK / uC = H(U) / log M
где H(U) - энтропия источника передаваемых сообщений, uK и u C - средние количества символов соответственно сообщения и кода передаваемых в единицу времени
µ = uK/ uC - среднее количество символов кода приходящиеся на одно сообщение

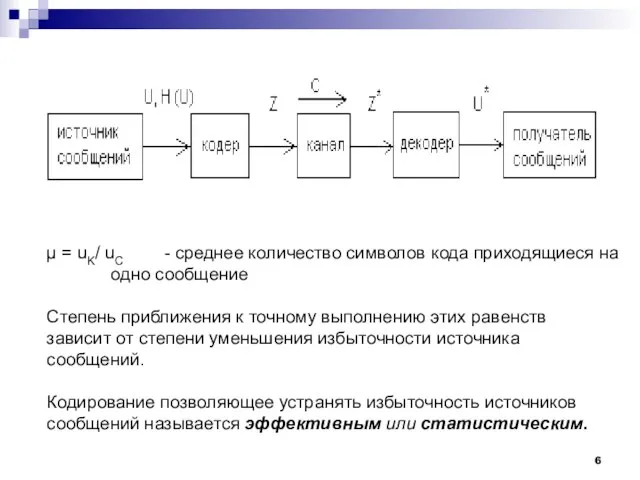
µ = uK/ uC - среднее количество символов кода приходящиеся на одно сообщение
Степень приближения к точному выполнению этих равенств зависит от степени уменьшения избыточности источника сообщений.
Кодирование позволяющее устранять избыточность источников сообщений называется эффективным или статистическим.

Избыточность дискретных источников обуславливается двумя причинами:
1) памятью источника;
2) неравномерностью сообщений.
Универсальным способом уменьшения избыточности обусловленной памятью источника является укрупнение элементарных сообщений.
При этом кодирование осуществляется длинными блоками. Вероятностные связи между блоками меньше чем между отдельными элементами сообщений и чем длиннее блоки, тем меньше зависит между ними

Пример. Рассмотрим источник, вырабатывающий два независимых символа с вероятностями 0,1 и 0,9. В этом тривиальном случае символы алфавита кодируются символами «0» и «1». Энтропия источника Н=0,469, средняя длина кодового слова равна 1,
избыточность источника и избыточность кода одинаковы и равны

1-я Теорема Шеннона
Предельные возможности статистического кодирования раскрывается в теореме Шеннона для канала без шума, которая является одним из основных положений теории информации.
Пусть источник сообщений имеет производительность H’U) = u C×H(U), а канал имеет пропускную способность C = uK ×log M. Тогда можно закодировать сообщения на выходе источника таким образом, чтобы получить среднее число кодовых символов приходящихся на элемент сообщения
µ = uK /uC = (H(U)/ log M)+ε
где ε- сколь угодно мало (прямая теорема)

1-я Теорема Шеннона
Получить меньшее значение µ невозможно
(обратная теорема).
Обратная часть теоремы утверждающая, что невозможно получить значение
µ = uK / uC < H(U)/ log M
Энтропия в секунду на входе канала или производительность кодера не может превышать пропускную способность канала)

1-я Теорема Шеннона
«Основная теорема о кодировании в отсутствие шумов»:
Среднюю длину кодовых слов для передачи символов источника А при помощи кода с основанием m можно как угодно приблизить к величине H(A) / log m.
теорема определяет нижнюю границу средней длины кодовых слов

Пример. Если источник без памяти имеет объем алфавита 32, то при равновероятных символах его энтропия равна 5 битам. Согласно теореме, для двоичного кода (m=2) наименьшая средняя длина кодового слова составляет H(A) / log m = 5, следовательно, код Бодо является оптимальным кодом для равновероятного источника без памяти.
Текст на русском языке, например, имеет энтропию около 2,5 бит, поэтому путём соответствующего кодирования можно увеличить скорость передачи информации вдвое против пятиразрядного равномерного кода Бодо

Практическое значение теоремы Шеннона заключается в возможности повышения эффективности систем передачи информации (систем связи) путем применения эффективного или экономного кодирования (кодирования источника).
Очевидно, что экономный код должен быть в общем случае неравномерным.
Общее правило кодирования источника (без памяти) состоит в том, что более вероятным символам источника ставятся в соответствие менее длинные кодовые слова (последовательности канальных символов).

Пример 8.5. Известный код Морзе служит примером неравномерного кода. Кодовые слова состоят из трех различных символов: точки ∙ (передается короткой посылкой), тире ― (передается относительно длинной посылкой) и пробела (паузы).
«е» “ ∙ ”
«ш» “ – – – – ”
Samuel Finley Breese Morse [mɔːrs] 1791 - 1872
Alfred Lewis Vail
1807 - 1859

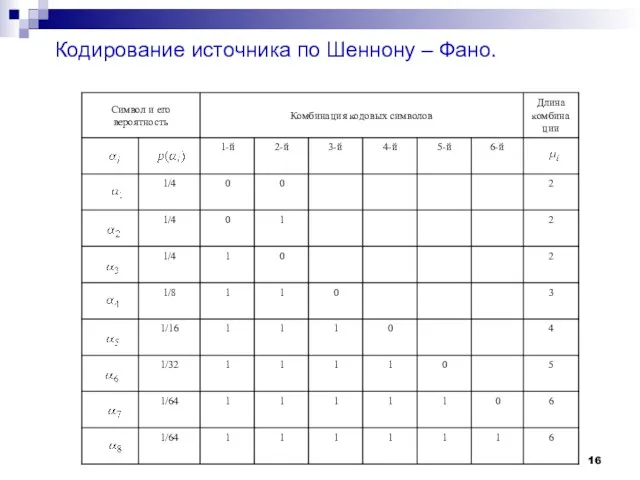
Кодирование источника по Шеннону – Фано.

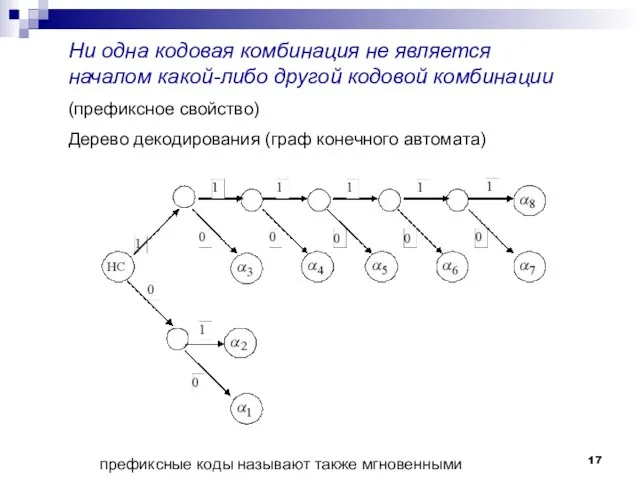
Ни одна кодовая комбинация не является началом какой-либо другой кодовой комбинации
(префиксное свойство)
Дерево декодирования (граф конечного автомата)
префиксные коды называют также мгновенными

Средняя длина кодовой комбинации для построенного кода
Согласно теореме Шеннона при оптимальном кодировании можно достичь средней длины
Заметим, что восемь различных символов источника можно представить восемью комбинациями равномерного двоичного кода (Бодо), при этом длина каждой кодовой комбинации равняется, очевидно, 3. Увеличение скорости передачи информации) составляет в данном примере около 22%.

Определим вероятность появления определенного символа в кодовой комбинации (пусть это будет
символ 1).
Её можно найти следующим образом:
а) подсчитать количества единиц во всех кодовых словах;
б) умножить эти количества на вероятности
соответствующих кодовых слов;
в) просуммировать полученные величины;
г) отнести результат к средней длине кодового слова.

при оптимальном кодировании источника кодовые символы равновероятны; такое кодирование является безызбыточным. Источник вместе с кодером можно рассматривать, как новый источник с алфавитом, состоящим из кодовых символов; энтропия и избыточность этого источника – это энтропия и избыточность кода. Оптимальный код имеет максимальную энтропию и нулевую избыточность.
ИС
К

Кодирование источника по Хаффману
Все символы алфавита записываются в порядке убывания вероятностей.
2. Два нижних символа соединяются скобкой, из них верхнему приписывается символ 0, нижнему 1 (или наоборот).
3. Вычисляется сумма вероятностей, соответствующих этим символам алфавита.
4. Все символы алфавита снова записываются в порядке убывания вероятностей, при этом только что рассмотренные символы «склеиваются», т.е. учитываются, как единый символ с суммарной вероятностью.
5. Повторяются шаги 2, 3 и 4 до тех пор, пока не останется ни одного символа алфавита, не охваченного скобкой.

Кодирование источника по Хаффмену

Энтропия алфавита .
Средняя длина кодового слова
=0,3⋅2+0,2⋅2+0,15⋅3+0,15⋅3+0,1⋅3+0,04⋅4+0,03⋅5+0,03⋅5=2,66
Вероятность символа 1 в последовательности кодовых комбинаций находится как среднее количество единиц, отнесённое к средней длине кодового слова
Избыточность кода равна 0.005

Оптимальность кода Шеннона – Фано в рассмотренном примере объясняется специально подобранными вероятностями символов, так, что на каждом шаге вероятности делятся ровно пополам.
В примерах предполагались источники без памяти. В реальных сообщениях на естественных языках символы не являются независимыми; в таких случаях следует кодировать не отдельные символы (буквы), а группы букв или слова. Это уменьшает зависимость и повышает эффективность кода.
Кодирование групп символов вместо отдельных символов также повышает эффективность кодирования в случае независимого источника с сильно различающимися вероятностями символов, как это видно из следующего примера.

Пример. Рассмотрим источник, вырабатывающий два независимых символа с вероятностями 0,1 и 0,9. В этом тривиальном случае методы кодирования Хаффмена и Шеннона – Фано приводят к одинаковому коду: символы алфавита кодируются символами «0» и «1». Энтропия источника Н=0,469, средняя длина кодового слова равна 1, избыточность источника и избыточность кода одинаковы и равны