Содержание
- 2. Сжатие информации представляет собой процесс преобразования исходного сообщения из одной кодовой системы в другую, в результате
- 3. Процесс восстановления называется декомпрессией или распаковкой и только после процесса распаковки данные пригодны для обработки в
- 4. Необратимое сжатие имеет гораздо более высокую степень сжатия, но допускает некоторые отклонения декодированных данных от исходных.
- 5. 3. Помехоустойчивое кодирование
- 9. Помехоустойчивое кодирование - предназначено для обнаружения и по возможности исправления ошибок, возникших вследствие действия помех при
- 10. Общим для всех трех видов кодирования является то, что информация каким-либо образом меняет форму представления, но
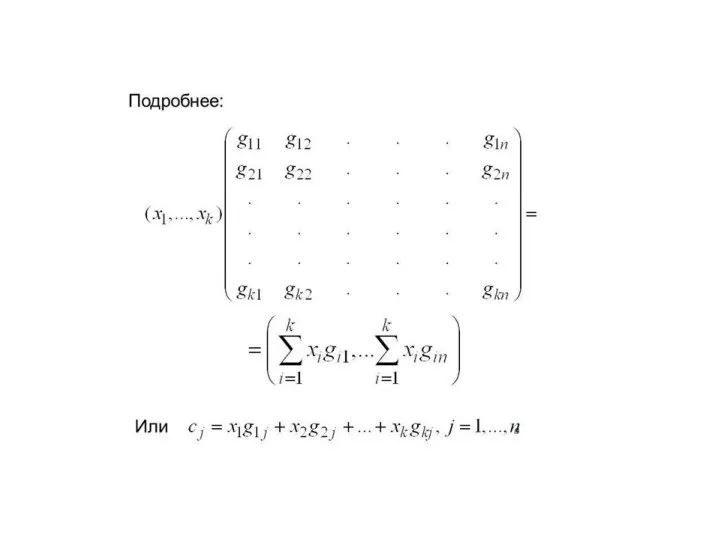
- 12. 2. Параметры кодов Число m используемых для кодирования элементарных символов, определяет основание кода. Коды с основанием
- 13. Расстоянием по Хэммингу между двумя кодовыми словами называется число разрядов, в которых они различны. При этом
- 14. Чтобы получить кодовое расстояние между двумя комбинациями двоичного кода, достаточно подсчитать число единиц в сумме этих
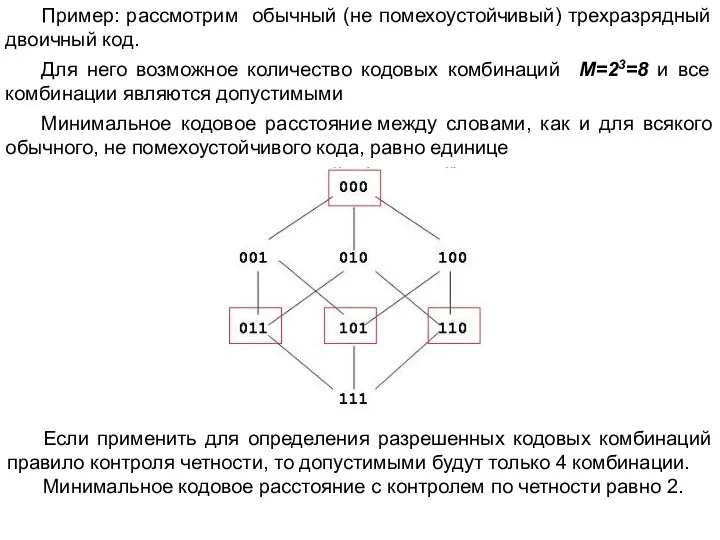
- 15. Пример: рассмотрим обычный (не помехоустойчивый) трехразрядный двоичный код. Для него возможное количество кодовых комбинаций M=23=8 и
- 16. Платой за помехоустойчивость является необходимость увеличения длины слов по сравнению с обычным кодом. В данном примере
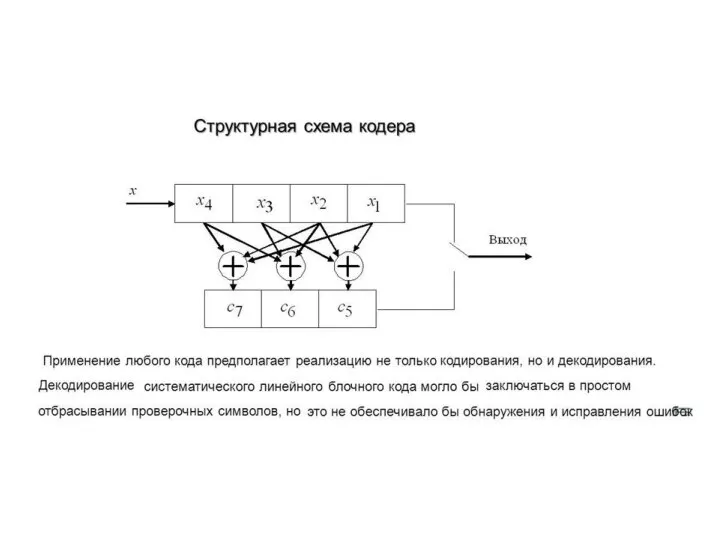
- 17. Таким образом, для того чтобы код мог обнаруживать и устранять ошибки, необходимо отказаться от его безызбыточности.
- 18. Введение дополнительных контрольных разрядов увеличивает затраты на хранение или передачу кодированной информации. При этом фактический объем
- 19. Чтобы код обладал свойствами обнаруживать одиночные ошибки, необходимо ввести избыточность, которая обеспечивала бы минимальное расстояние между
- 20. 2. Для исправления одиночной ошибки каждой разрешенной кодовой комбинации необходимо сопоставить подмножество запрещенных кодовых комбинаций. Чтобы
- 21. Для ориентировочного определения необходимой избыточности кода при заданном кодовом расстоянии d можно воспользоваться верхней граничной оценкой
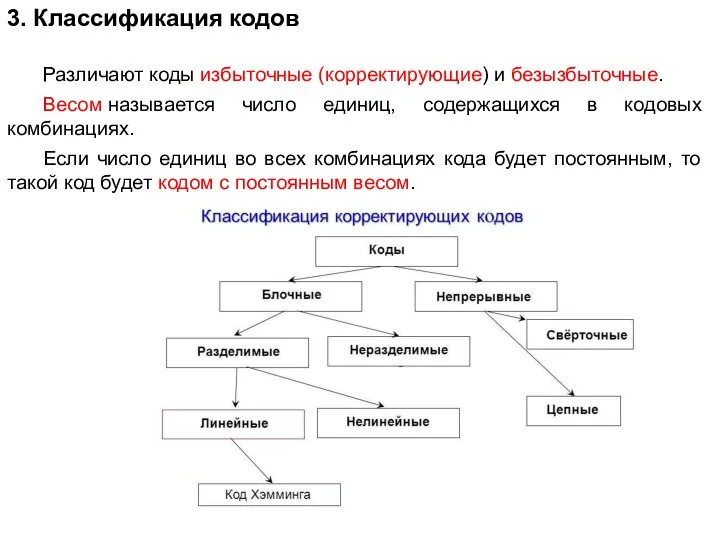
- 22. 3. Классификация кодов Различают коды избыточные (корректирующие) и безызбыточные. Весом называется число единиц, содержащихся в кодовых
- 23. Равномерные и неравномерные коды. У равномерных кодов n=const, например, пятиразрядный код Бодо. У неравномерных кодов n
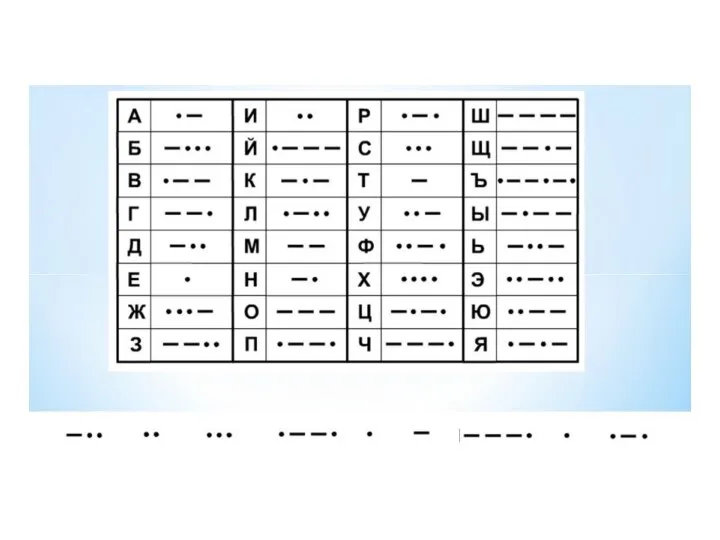
- 25. Код Морзе статистически согласован с английским языком. Так буква Е, которая в английском языке имеет наибольшую
- 26. Неравномерность является основной особенностью кода Морзе, которая позволяет учитывать статистику сообщения. Однако код Морзе менее экономичный,
- 27. Неравномерность кода Морзе не позволяет осуществить слитную передачу кодовых комбинаций, а следовательно, и осуществить кодом Морзе
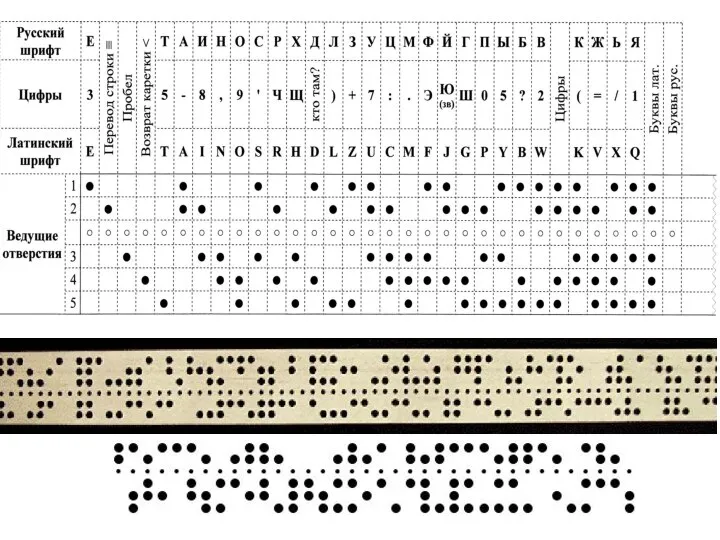
- 28. Код Бодо
- 30. Равномерные корректирующие коды подразделяются на блочные и непрерывные. В блочных двоичных кодах последовательность элементарных сообщений источника
- 31. Среди помехоустойчивых кодов выделяют разделимые коды и неразделимые коды. В разделимых кодах разряды могут быть принципиально
- 32. Для систематического кода применяется обозначение (n,m)–код, где n – число всех разрядов в кодовой комбинации, m
- 44. Циклические коды относятся к блоковым кодам. Последовательность кодовых комбинаций в циклическом коде разбивается на отдельные блоки,
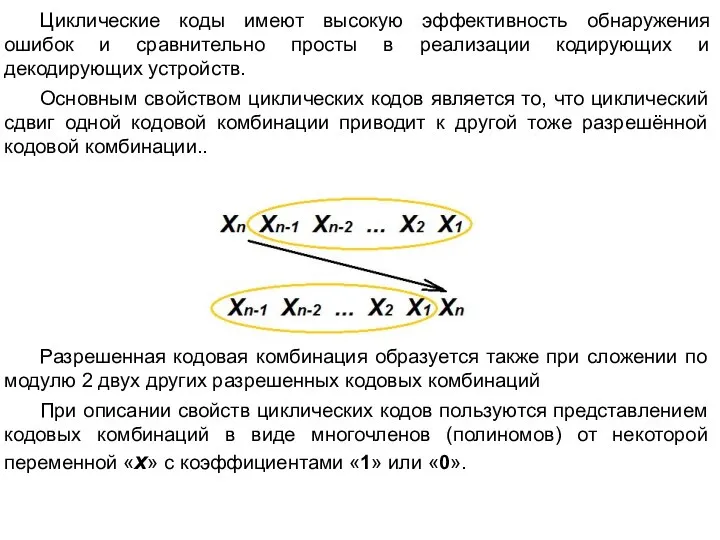
- 45. Циклические коды имеют высокую эффективность обнаружения ошибок и сравнительно просты в реализации кодирующих и декодирующих устройств.
- 46. Цифры двоичного кода можно рассматривать как коэффициенты многочлена переменной х. Например, для кодовой комбинации 1011011 (n=7)
- 47. Принцип обнаружения ошибок при помощи циклического кода заключается в том, что в качестве разрешенных кодовых комбинаций
- 48. Построение комбинаций циклического кода возможно путем умножения исходной комбинации А(х) на образующий полином G(x) с приведением
- 49. В процессе кодирования сообщения: Mногочлен А(x), отображающий двоичный код исходного передаваемого сообщения, умножается на хk. При
- 50. Пример. Дано: n=7, m=4, k=3 и G(x)=x3+x2+1. Требуется закодировать сообщение 1 0 1 1. Cообщению 1011
- 51. При применении циклического кода в качестве кода с исправлением ошибок места искаженных разрядов определяются путем анализа
- 52. 5. Код Хемминга Ричард Хемминг разработал код, который обеспечивает обнаружение и исправление одиночных ошибок при минимально
- 53. Рассмотрим пример, когда количество информационных бит m в блоке равно 4. Это код (7,4), количество проверочных
- 54. Построение корректирующего кода Хэмминга производится исходя из требуемого объема информационных сообщений и статистических данных о наиболее
- 55. Значения символов в проверочных разрядах устанавливаются в результате суммирования по модулю 2 значений символов в определенных
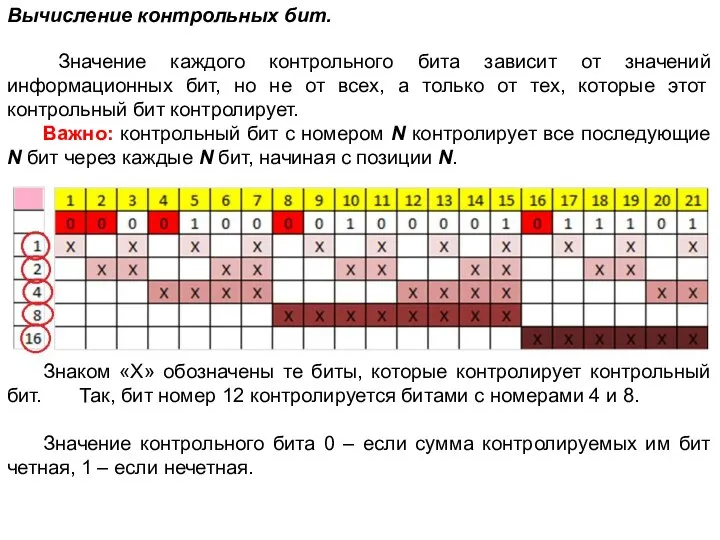
- 56. Вычисление контрольных бит. Значение каждого контрольного бита зависит от значений информационных бит, но не от всех,
- 57. Проверка на приемной стороне принятой кодовой комбинации осуществляется следующим образом: создаются контрольные суммы S1, S2, S3,
- 58. Сущность обнаружения позиции ошибки, а значит и ее исправления кодом Хэмминга состоит в том, что производятся
- 59. . Пример. Построить код Хэмминга с исправлением одиночной ошибки при 11 информационных разрядах, т.е. m=11. Определим
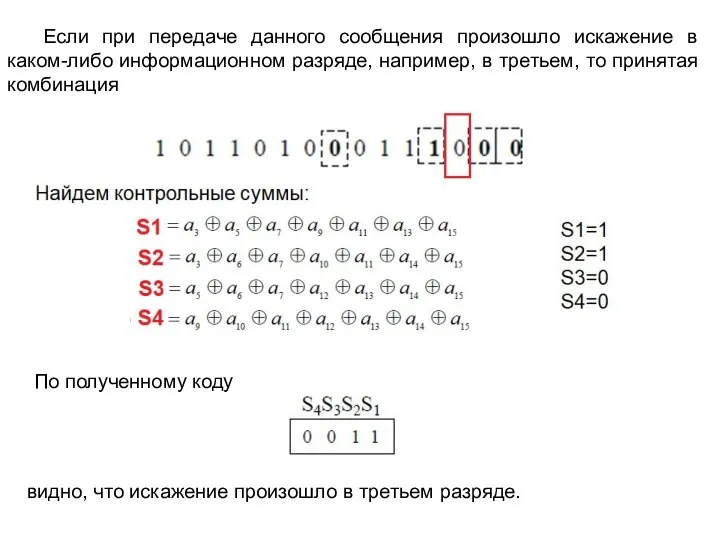
- 60. Если при передаче данного сообщения произошло искажение в каком-либо информационном разряде, например, в третьем, то принятая
- 61. 6. Коды Рида-Соломона Коды Рида-Соломона были предложены в 1960 сотрудниками Линкольнской лаборатории МТИ Ирвином Ридом и
- 63. Скачать презентацию


















































 Знакомство с Visual Studio
Знакомство с Visual Studio Информационные системы и автоматизация информационных процессов
Информационные системы и автоматизация информационных процессов Выдача компьютера: создание заявки
Выдача компьютера: создание заявки Создание и заполнение баз данных. 9 класс
Создание и заполнение баз данных. 9 класс Интернет-проект История.ру
Интернет-проект История.ру Применение и наладка протоколов маршрутизации TCP, UDP, SCTP
Применение и наладка протоколов маршрутизации TCP, UDP, SCTP Свинограм
Свинограм Вставка в документ художественного текста и рисунков
Вставка в документ художественного текста и рисунков Проводник пассажирского вагона 3-го разряда с использованием социальной сети ВКонтакте
Проводник пассажирского вагона 3-го разряда с использованием социальной сети ВКонтакте Инструкция по обновлению навигационного ПО Hyundai Creta (GSr) with SD card
Инструкция по обновлению навигационного ПО Hyundai Creta (GSr) with SD card Программирование линейных алгоритмов. Начала программирования
Программирование линейных алгоритмов. Начала программирования Программирование в среде Robot C. Занятие 10: Структурное программирование
Программирование в среде Robot C. Занятие 10: Структурное программирование Формы мышления. Алгебра высказываний. Логические выражения и таблицы истинности
Формы мышления. Алгебра высказываний. Логические выражения и таблицы истинности Оператор Ввода
Оператор Ввода Презентация МДК
Презентация МДК Хищники. Культура и биология
Хищники. Культура и биология Правила поведения в чатах
Правила поведения в чатах Қазақстандағы байланыс қуралдарынын дамуы
Қазақстандағы байланыс қуралдарынын дамуы Устройства ввода графической информации. Итоговое тестирование
Устройства ввода графической информации. Итоговое тестирование Кодировка символов. Символьный тип. Строковые функции. Примеры. Лекция 4
Кодировка символов. Символьный тип. Строковые функции. Примеры. Лекция 4 Моделирование объектов виртуальной экспериментальной установки для лабораторной работы
Моделирование объектов виртуальной экспериментальной установки для лабораторной работы Сохранение сметы
Сохранение сметы Знаки и знаковые системы
Знаки и знаковые системы Путешествие в страну Занимательной грамматики
Путешествие в страну Занимательной грамматики Алгоритмы и их свойства
Алгоритмы и их свойства Tsoy
Tsoy Создание модели компьютерного класса будущего
Создание модели компьютерного класса будущего Принцип организации и преимущества колонки-ориентированной со сжатым словарем базы данных в памяти
Принцип организации и преимущества колонки-ориентированной со сжатым словарем базы данных в памяти