Слайд 2 ЛК № 6-7
Каждая функция имеет имя и один или несколько

аргументов, заключенных в круглые скобки, например, = СУММ(А1:А3). Некоторые функции не имеют аргументов, например,= ПИ(), = СЕГОДНЯ().
При использовании в функции нескольких аргументов они отделяются один от другого ( ; ), например =ПРОИЗВЕД(С1;C3;C6). В функции можно использовать до 30 аргументов, при общей длине формулы менее 1024 символа.
В качестве аргум-ов ф-ции могут быть использованы:
1. Диапазон, содержащий произвольное число ячеек листа. Например, = СУММ(А1:A3;C2:C10;D3:D11). Ф-ция имеет три аргумента, но суммирует числа в 21 ячейке.
Слайд 3 ЛК № 6-7
При этом указанные в ссылке ячейки могут содержать

формулы.
2. Выражения, содержащие функции или их набор. Комбинацию функций можно использовать для создания выражения, которое в дальнейшем будет использоваться как аргумент. Например, =СУММ(SIN(A1*ПИ());2*COS(ПИ())) , где SIN(A1*ПИ()) и 2*COS(ПИ()) - выражения, которые
используются в качестве аргументов.
3. Числовые значения. Например, =СУММ(110;19;45)
4. Текстовые значения. Например, =ТЕКСТ(ТДАТА;"Д МММ ГГ"), где Д МММ ГГ текстовый аргумент т.к. в " ". Возвращаемое этой функцией значение 24 фев 2003.
Слайд 4 ЛК № 6-7
5. Логические значения. Аргументы ряда функций могут принимать

логические значения ИСТИНА или ЛОЖЬ ( не путать с функциями ИСТИНА(), ЛОЖЬ() ). Например, ячейка А1 может принимать значения ИСТИНА или ЛОЖЬ, то можно составить уравнение: =ЕСЛИ(А1=ИСТИНА;"Новый год";"Старый год") , где А1=ИСТИНА - логическое выражение. {А2=2 А3=1 в яч. А1 введем =А2>А3, в яч. А1 отобразится ИСТИНА.}.
6. Имена диапазонов. Присвоим диапазону А1:А6 имя Кредит, тогда используем формулу =СУММ(Кредит).
Слайд 5 ЛК № 6-7
7. Массивы. Например, {=ЦЕЛОЕ(А1:С7}
8. Различные типы аргументов.

Например, =СРЗНАЧ(Кредит;А8;2*7) , где Кредит - диапазон ячеек, А8-ячейка, 2*7 - числовое значение.
2) Группы встроенных функций
Выделим восемь групп встроенных функций. Приведем синтаксис некоторых из них. Дополнительную инф-цию о функциях можно найти в специальной литературе.
А) Функции дат =СЕГОДНЯ() - возвращает десятичное значение текущей даты; =ТДАТА() - возвращает текущее значение даты и времени; =ГОД(десятичная дата); =МЕСЯЦ(десятичная дата);
Слайд 6 ЛК № 6-7
=ДЕНЬ(десятичная дата) --эти три функции возвращают год, месяц,

день для заданного значения даты =ДОЛЯГОДА(начальная дата; конечная дата; базис) --вычисляет десятичное значение, представляющее собой часть года, которую составляет интервал между двумя заданными датами;
Б) Функции времени =ЧАС(десятичная дата); =МИНУТЫ(десятичная дата); СЕКУНДЫ(десятичная дата) -- они возвращают час, минуты, секунды для заданного значения времени.
2. Математические функции
Это: =СУММ(числа); различные модификации ф-ций округления вниз, вверх , до ближайшего целого и т.д.
Слайд 7 ЛК № 6-7
В ряду математических ф-й можно выделить: Логарифмические :

LOG, LOG10, LN, EXP и СТЕПЕНЬ
Тригонометрические: ПИ(), SIN,COS, ГРАДУСЫ, РАДИАНЫ
Инженерные: они разделяются на три основные группы: -функции для работы с комплексными числами;
-ф-ции для преобразования между различными системами счисления (двоичной, десятичной и т.д.)
-различные формы функций Бесселя.
3. Текстовые функции
Они преобразуют числовые текстовые значения в числа и числовые значения в строки символов (текстовые строки), а также позволяют выполнять над строками символов
Слайд 8 ЛК № 6-7
различные операции.
=ДЛСТР(текст)--возвращает количество символов в текстовой строке; {=ДЛСТР(“123456”)

возвращает число 6}.
=СИМВОЛ(число) –возвращает символ, который соответствует заданному числовому коду ASCII
{=СИМВОЛ(89)- возвращает символ Y}
=СОВПАД(текст1;текст2)-- сравнивает две строки текста на полную идентичность с учетом регистра букв; =ПОВТОР(текст; число повторений)-- позволяет заполнить ячейку строкой символов, повторенной заданное число раз.
4. Логические функции
Это: =ЕСЛИ(логическое выражение;значение если истина;значение если ложь); Вложенные функции ЕСЛИ
Слайд 9 ЛК № 6-7
(допускается до семи уровней вложения);
=И(лог. зн.1;лог. зн.2;…лог.

зн.30)
=ИЛИ(лог. зн.1;лог. зн.2;…лог. зн.30)
=НЕ(лог. зн.).
Большинство логических функций используют логические выражения, например =А1>А2.
5. Функции просмотра и ссылок
Они позволяют "просматривать " информацию, хранящуюся в списке или таблице и обрабатывать ссылки.
=ВЫБОР(номер индекса;зн.1; зн.2;…зн.29)-возвращает значение из списка аргументов;
Если в А2=4, а в яч. А1=ВЫБОР(А2;2;3;4;5;6) А1=5
Функции ВПР и ГПР имеют одинаковый синтаксис и предназначены для поиска данных (чисел, текста)
Слайд 10 ЛК № 6-7
соответственно в вертикальной и горизонтальной таблице.
=ВПР(искомое значение; таблица;номер

столбца;тип просмотра);
=ИНДЕКС(массив;номер строки;номер столбца) --возвращает значение элемента массива, заданного номером строки и номером столбца;
6. Финансовые функции
Они позволяют выполнять обычные финансовые вычисления. Эту группу можно разделить на четыре подгруппы. Приведем без синтаксиса некоторые из них.
6.1. Функции для анализа инвестиций. Это: НПЗ- чистая текущая стоимость, ППЛАТ- вычисляет размер периодической выплаты, необходимый для погашения ссуды за указанное число периодов.
Слайд 11 ЛК № 6-7
6.2. Функции для вычисления скорости оборота. Это: НОРМА-

позволяет определять скорость оборота.
6.3. Функции для вычисления амортизации. Это: АМР, ДДОБ, ДОБ -позволяют определять величину амортизации имущества за заданный период.
6.4. Функции для анализа ценных бумаг. Это: ИНОРМА -вычисляет процентную ставку для полностью инвестированных ценных бумаг, СКИДКА- вычисляет скидку для ценных бумаг.
7. Статистические функции
Это: СРЗНАЧ, МЕДИАНА, МОДА, ЛИНЕЙН, РОСТ, ТЕНДЕНЦИЯ и др. будут рассмотрены в дальнейшем.
8. Статистические функции баз данных
Эти функции предназначены для работы со списками. Их 14:СЧЕТЕСЛИ, СУММЕСЛИ, БДСУММ и т.д.
Слайд 12 ЛК № 6-7
3) Массивы
Под массивом в Excel понимается прямоугольный диапазон

формул и значений, которые программа обрабатывает как единую группу.
Например, диапазон С2:С5 – есть массив данных. Создать формулу массива значит выполнить какую либо операцию над массивом. Например, массив С2:С5 умножим на число 125, т.е. создадим формулу массива: {=С2:С5*125}
Excel позволяет работать с массивом 200х200.
Формула массива использует несколько множеств значений, называемых массивами аргументов. Например, С2:С5 – массив аргументов.
Слайд 13 ЛК № 6-7
В качестве аргументов могут быть использованы:
Диапазон ячеек D2:D8
Массив

констант. Он должен заключаться во внутренние фигурные скобки, а элементы массива, находящиеся в разных столбцах должны разделяться (;), а разных строках – (:). (3 строки, 4 столбца)
{=КОРЕНЬ({14;9;16;25:36;49;64;82:100;121;144;169)}}
Имя диапазона или массива
Массивы бывают:
Одномерные(горизонтальные A1:G1, вертикальн.A1:A9)
Двумерные (А1:С3)
Слайд 14 ЛК № 6-7
Действия с массивами:
Массивы можно умножать и делить на

число, к массивам можно прибавлять и вычитать числа.
С несколькими массивами можно выполнять арифметические операции, т.е. Поэлементное сложение, вычитание, деление и умножение.
Необходимо помнить, что для фиксации ввода формулы массива необходимо нажать комбинацию клавиш Ctrl+Shift+Enter.
Для работы с массивами имеются специальные встроенные функции.
=МОБР(массив) – возвращает обратную матрицу
Слайд 15 ЛК № 6-7
=МОПРЕД(массив) – возвращает определитель матрицы
=МУМНОЖ(массив1;массив2) - возвращает матричное

произведение двух матриц
=ТРАНСП(массив) – возвращает транспонированную матрицу.
Слайд 16 ЛК № 6-7
Финансовый анализ в Excel
Вопросы:
1. Функции для анализа инвестиций

и вычисления скорости оборота
2. Функции для вычисления амортизации.
3. Функции для анализа ценных бумаг
Финансовые функции можно разделить на:
-Функции для анализа инвестиций
∙ -Функции для вычисления скорости оборота
∙ -Функции для вычисления амортизации
∙ -Функции для анализа ценных бумаг
Рассмотрим каждую из этих подгрупп.
Слайд 17 ЛК № 6-7
1) Функции для анализа инвестиций и вычисления скорости

оборота
Инвестиционный проект (ИП) - это долгосрочный план вложения средств предприятий, фирм и т.д. в такие активы, как оборудование, здания, землю, технологии и т.п. и получение доходов от этих вложений.
В каждом периоде времени ИП предполагает как доходы, так и расходы. Т.е. ИП порождает поток денежных средств. Расчеты по инвестиционной деятельности, как правило, выполняются за промежуток времени, равный году.
Для оценки инвестиционных проектов применяются разные критерии. Одним из них является метод чистой текущей стоимости. Рассмотрим его.
Метод чистой текущей стоимости.
Слайд 18 ЛК № 6-7
Чистую текущую стоимость обозначают аббревиатурой NPV.
, где
С0,

С1 …, Сn - поток платежей в годы t= 0,1,…, n. При этом знак Сt может быть как положительным так и отрицательным.
r- ставка дисконтирования, процентная ставка (в качестве которой может быть принята ставка прибыли).
Для анализа проектов по этому методу используется функция НПЗ(ставка;плата1;плата2;…плата29), где ставка - процентная ставка за период,%, плата1…плата29 - аргументы, определяющие доходы и расходы.
Функция НПЗ возвращает чистую текущую стоимость вклада, которая представляет собой сегодняшний объем
Слайд 19 ЛК № 6-7
будущих платежей (отрицательные значения) и поступлений (положительные значения).

Т.е предполагаемый доход от вклада требуется пересчитать на настоящее время.
Необходимо учитывать две вещи:
не включать первоначальные инвестиции (сделанные в момент 0) в поток платежей
вычесть величину первоначальных инвестиций из полученного значения функции НПЗ.
Если НПЗ отрицательна, то принимать такой проект не имеет смысла. Из нескольких проектов следует принимать тот, который имеет более высокое значение НПЗ при одной и той же ставке дисконтирования.
Полным аналогом ф-ции НПЗ, является ф-ция ЧИСТПЗ, вычисляющая стоимость потока платежей, осуществля-
Слайд 20 ЛК № 6-7
емых, через произвольные промежутки времени. Ф-ция имеет синтаксис:

ЧИСТПЗ(ставка;платежи;дата).
Более сложным аналогом ф-ции НПЗ является функция ПЗ. Ее синтаксис:
ПЗ(ставка;кпер;выплата;бз;тип) где
Ставка - процентная ставка за период
Кпер - общее число периодов выплат
Выплата - величина постоянных периодических платежей
Бз - будущая стоимость или баланс наличности, который нужно достичь после последней выплаты.
Тип - число, равное 0 или 1, обозначающее когда должна производиться выплата. 1- в начале, 0 - в конце периода или если этот аргумент опущен.
Слайд 21 ЛК № 6-7
Отличие ф-ции ПЗ от НПЗ состоит в следующем

:
А) ф-ция ПЗ предполагает значения выплат постоянными, а НПЗ допускает использование выплат переменной величины
Б) ПЗ допускает поток платежей как в начале, так в конце периода, а НПЗ предполагает, что поток платежей равномерно распределен по годам и производится в конце периода.
Функция НПЗ тесно связана с ф-ей которая возвращает внутреннюю скорость оборота (ВНДОХ) и относится ко 2-ой подгруппе функций.
Функция ВНДОХ возвращает скорость оборота , для которой значение функции НПЗ равняется нулю, т.е. НПЗ(ВНДОХ(…);…)=0.
Функция ВНДОХ (IRR)имеет синтаксис:
Слайд 22 ЛК № 6-7
ВНДОХ(значение;прогноз), где
Значение - массив или ссылка на ячейки,

содержащие числовые величины, для которых вычисляется внутренняя скорость оборота средств.
Прогноз - величина, о которой предполагается, что она близка к результату ВНДОХ. Это необязательный аргумент. Если он не указан, то по умолчанию он равен 10%.
Экономический смысл функции ВНДОХ состоит в следующем.
Если ИП состоит из потока платежей: С0, С1, .., Сn и платеж Сt происходит в год t (t=0,1,…n), то ставка прибыли (процентная ставка) r является корнем уравнения:
Слайд 23 ЛК № 6-7
т.о. внутренняя скорость оборота - это ставка, при

которой текущая стоимость (NPV) поступлений от вложения равна стоимости вложения.
Использование вышеприведенных ф-ций может осуществляться по трем направлениям:
1. Когда дан поток платежей и барьерная процентная ставка (%).
Пример 1. Есть возможность вложения авансом на четыре года 250 000 при процентной ставке 12%. При этом в конце каждого года получим:
1-ый год - убыток 55 000
2-ой год - прибыль 95 000
3-й год - прибыль 140 000
4-й год - прибыль 185 000
Тогда ф-я НПЗ может быть записана:
Слайд 24 ЛК № 6-7
= НПЗ(12%; -55000;95000; 140000; 185000)-- 250000.
Результат

равен - 6153,65,а т.к. знак минус, то вы не можете рассчитывать на прибыль по данному проекту.
Пример 2. Можно вложить сегодня 4 000, и в течение пяти лет получать ежегодно по 1 000. Выгодно это или нет? Полагая, что деньги можно положить под процент в банк (4,5%), возьмем его в качестве ставки прибыли («барьера»).
Тогда, ф-я =ПЗ(4,5%;5;1000) возвратит минус 4390, означающее, что если вложить 4390 теперь (при 4,5%), то через 5 лет получим 5 000. Значит наши вложения выгодны, т.к. мы вкладываем 4 000.
Пример 3. Можно вложить сегодня 4 000, и в конце пятого года получать 5 000. Выгодно это или нет?
Процентная ставка 4,5%. Тогда ф-я =ПЗ(4,5%;5;;5000).
Слайд 25 ЛК № 6-7
возвратит текущую стоимость минус 4012.Т.е. выгодно, но не

очень.
2. Когда дан поток платежей и требуется определить процентную ставку, при которой сделка дает прибыль. Для этого используется команда Подбор параметра.
Пример. =НПЗ(А1;А2:А5), где в ячейке А1 в результате подбора параметра отобразится искомый процент. В ячейки А2:А5 вводятся значения потока платежей (по годам).
3. Когда даны платежи и требуется определить “барьерную” процентную ставку, т.е. ставку когда прибыль равна первоначальным вложениям.
Пример. Вы вкладываете в предприятие 120 000. В течение следующих пяти лет вы ожидаете получить прибыль 25 000, 27 000, 35 000, 38 000, 40 000. Тогда функция
=ВНДОХ({-120000; 25000;27000;35000;38000;40000}) или
Слайд 26 ЛК № 6-7
=ВНДОХ(А1:А6), если данные введены в ячейки А1,А2…А6,

возвратит внутреннюю скорость оборота, равную 11%. Т.о. если барьерная ставка (процентная ставка банка) равна 10%, то вложение денег выгодное.
2) Функции для вычисления амортизации
Под амортизацией понимается уменьшение стоимости имущества в процессе эксплуатации. Обычно оценивают величину этого уменьшения на единицу времени(в частности месяца).
Суммы, на которые уменьшается стоимость имущества, называются амортизационными отчислениями (АО). Владелец налогооблагаемого имущества заинтересован в быстром уменьшении его балансовой стоимости и переноса ее на себестоимость продукции, т.к. это ведет к снижению налога на имущество.
Слайд 27 ЛК № 6-7
Различные способы расчета АО
2.1.Равномерная (линейная) амортизация.
Если срок

службы имущества равен n годам и первоначальная стоимость его S, то ежегодно стоимость уменьшается на S/n или (100/n)%. Следовательно величина ежегодных АО равна S/n. Стоимость имущества в конце К-того года Sk вычисляется по формуле:
, где К=1,2,…..n.
Для расчета амортизации за один период используется функция: =АМР(стоимость; остаток; срок), где
стоимость- первоначальная стоимость
остаток- остаточная стоимость полной амортизации (ликвидная стоимость)
Слайд 28 ЛК № 6-7
срок- количество периодов, за которые имущество амортизируется(лет).
2.2.

Правило суммы лет.
Известно, что износ оборудования обычно идет больше в начале срока службы, так например, автомобиль изнашивается больше в первые годы эксплуатации.
Поэтому разработаны методы ускоренной амортизации, к которым и относится правило суммы лет.
Для него величина АО в i-том году для срока амортизации равного n лет равна:
, где S-первоначальная стоимость
имущества
Kn-сумма номеров лет, т.е. Kn=1+2+3+…+n=n(n+1)/2
Слайд 29 ЛК № 6-7
АО по правилу суммы лет -- убывающая функция.
Для

расчета используется встроенная функция:
=АМГД(стоимость; остаток; срок; период),
стоимость, остаток, срок- имеют описание аналогичное для функции АМР.
Период- номер периода для вычисления амортизации (д.б. измерен в тех же единицах, что и аргумент срок).
Пример. Определить по годам АО оборудования с начальной стоимостью 15 000, сроком амортизации 3 года и остаточной стоимостью 1 250.
АО в 1-й год =АМГД(15 000;1250;3;1) равны 6 875.
АО во 2-ой год =АМГД(15 000;1250;3;2) равны 4 583.
АО в 3-й год =АМГД(15 000;1250;3;3) равны 2 292.
Итого: 15 000
Слайд 30 ЛК № 6-7
2.3.Методы фиксированного и двойного процента.
При расчете АО по

методу фиксированного процента вначале определяется фиксированная ставка процента(r), на которую снижается остановочная стоимость имущества каждый год. Для этого используется формула:
, где S-первоначальная стоимость имущества
S0-остаточная стоимость имущества
n- срок службы имущества
Затем по нижеприведенной формуле определяются АО.
АО=r* (стоимость на конец года)
Функция, производящая расчет по методу фиксирован- ного процента имеет синтаксис:
Слайд 31 ЛК № 6-7
ДОБ(стоимость; остаток; срок; период; месяц), где месяц -

количество месяцев в первом году(по умолчанию этот аргумент равен 12).
Суть метода двойного процента: фиксированный процент (r) принимается равным удвоенному проценту снижения стоимости при равномерной амортизации.
Для расчета АО по методу двойного процента используется следующие функции:
ДДОБ(стоимость; остаток; срок; период; коэффициент)
ПДОБ(стоимость; остаток; срок; начало; конец; коэффициент; переключение), где аргументы
коэффициент и переключение - необязательные аргументы
Пример 1. Начальная стоимость – 1 000 000.
Слайд 32 ЛК № 6-7
Остаточная стоимость - 100 000.
Срок службы - 6

лет
Первый год службы - 7 месяцев
Определить АО за первый год (период).
=ДОБ(1 000 000;100 000;6;1;7) равно 186 083.
=ДДОБ(1 000 000;100 000;6;1) равно 333 333.
Пример 2. В конце 1-го квартала приобрели имущество на сумму 15 000.
Срок службы – 5 лет.
Остаточная стоимость – 2 000.
Определить АО за следующий год(с 4-го по 7-й квартал)
=ПДОБ(15 000;2 000;20;3;7) равно 3 671.
Слайд 33 ЛК № 6-7
3) Функции для анализа ценных бумаг
Ценная бумага (ЦБ)

– форма существования капитала, отличная от его товарной, производительной и денежной форм, которая может передаваться вместо него самого, обращаться на рынке как товар и приносить доход.
Эмитент – продавец ЦБ
Инвестор – покупатель ЦБ
Основные ценные бумаги.
3.1. Акции – ЦБ, закрепляющая права владельца на получение части прибыли акционерного общества(АО) в виде дивидендов, на участие в управлении АО и на часть имущества, после его ликвидации.
К выпуску акций эмитента привлекает следующее:
АО не обязано возвращать инвесторам их капитал, вложенный а покупку акций
Слайд 34 ЛК № 6-7
Выплата дивидендов не гарантируется
Размер дивидендов может устанавливаться

произвольно
Инвестора привлекает:
Право голоса на вложенный капитал
Право на доход, в виде дивидендов и т.д.
3.2. Облигации – ЦБ, которая предоставляет ее держателю право на получение фиксированного процента от номинала.
Особенности облигаций
Инвестор не пользуется правами собственника(отличие от акций)
Инвестор гарантированно получает прибыль в виде процентов и т.д.
3.3. Государственные ценные бумаги и т.д.
Слайд 35 ЛК № 6-7
Функции для анализа ценных бумаг
Аргумент Описание
Базис – способ

вычисления дня (1-фактический)
Частота - количество выплат в год (1-ежегодная, 2-полугодовая , 4- ежеквартальная)
Выпуск - дата выпуска ценных бумаг
Погашение - дата погашения ценных бумаг
Номинал – номинальная стоимость ценных бумаг
Ставка-процентная ставка по ЦБ на дату выпуска
Сделка- дата сделки(день оплаты) с ЦБ
Доход- годовой доход по ЦБ
Выкуп –стоимость ЦБ при погашении (за 100 р. нар.ст.)
Цена- цена за 100 р.($) нарицательной стоимости ЦБ
Ф –я НАКОПДОХОД возвращает накопленный доход по ценным бумагам с периодической выплатой процентов.
Слайд 36 ЛК № 6-7
=НАКОПДОХОД(выпуск;дата первой выплаты; сделка;ставка;номинал;частота;базис)
Ф-я ДОХОД определяет годовой доход

по ЦБ с периодической выплатой процентов.
=ДОХОД( сделка;погашение;ставка;цена;выкуп; частота; базис)
Ф-я Цена вычисляет цену за 100 руб($) нарицательной стоимости ЦБ
=ЦЕНА(сделка;погашение;ставка;доход;выкуп; частота;базис)
Ф-я НАКОПДОХОДПОГАШ возвращает накопленный доход по ЦБ с периодическим начислением процентов, выплата которых производится при погашении.



































 Cпособы обтравки изображений
Cпособы обтравки изображений Библиотеки Python
Библиотеки Python Путешествуем по графу
Путешествуем по графу Особенности репрезентации римской темы в российской социальной сети Вконтакте
Особенности репрезентации римской темы в российской социальной сети Вконтакте Образовательные сайты в Интернете
Образовательные сайты в Интернете Shox International Hospital. Международная больница Шокс
Shox International Hospital. Международная больница Шокс Разработка информационной панели (dashboard) ключевых показателей деятельности органов исполнительной власти субъекта РФ
Разработка информационной панели (dashboard) ключевых показателей деятельности органов исполнительной власти субъекта РФ Кодирование информации
Кодирование информации Обработка текстовой информации
Обработка текстовой информации Введение в программирование
Введение в программирование От персонального компьютера к персональному производству
От персонального компьютера к персональному производству ВКР: Автоматизация расчетов с поставщиками и подрядчиками Steak at home
ВКР: Автоматизация расчетов с поставщиками и подрядчиками Steak at home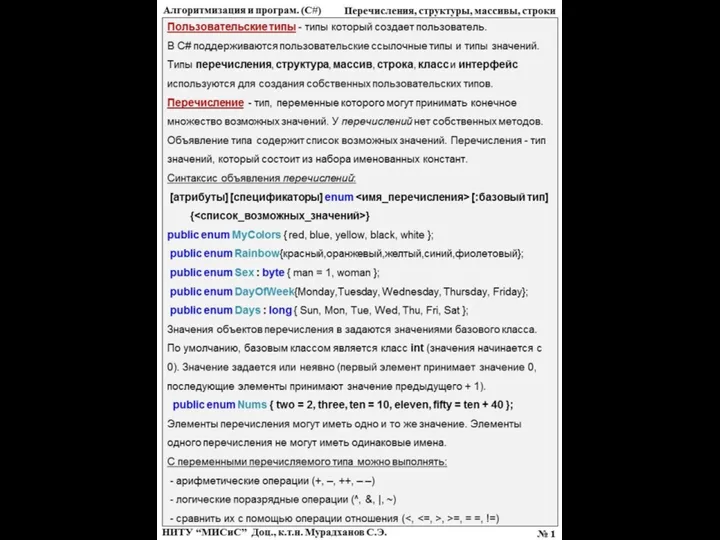 Алгоритмизация и программирование С#. Перечисления, структуры, массивы, строки. (Лекция 6)
Алгоритмизация и программирование С#. Перечисления, структуры, массивы, строки. (Лекция 6) АС мониторинг оборудования в сети и базы данных
АС мониторинг оборудования в сети и базы данных Системы кадровой синхронизации
Системы кадровой синхронизации Objektorientierte. Modul 24
Objektorientierte. Modul 24 Python. База данных: консольный интерфейс
Python. База данных: консольный интерфейс Поколения компьютеров
Поколения компьютеров Страна информатика
Страна информатика Аналитические публицистические жанры
Аналитические публицистические жанры Проектирование сети поставщика интернет-услуг
Проектирование сети поставщика интернет-услуг Векторная графика. Задания
Векторная графика. Задания Игра – конкурс по информатике
Игра – конкурс по информатике Сервис для определения вашей схожести со звездами
Сервис для определения вашей схожести со звездами ArtCAМ. Размер новой модели
ArtCAМ. Размер новой модели Защита персональных данных
Защита персональных данных Тематический календарь 2020
Тематический календарь 2020 Baby Blog. ru
Baby Blog. ru