Содержание
- 2. Цель и задачи Цель презентации: изучение и закрепление знаний о комбинаторике. Задачи презентации: 1. Отыскать информацию
- 3. . Комбинаторика Комбинаторика -- это область математики, прежде всего связанная с подсчетом, как средство и цель
- 4. Функция, определённая на множестве неотрицательных целых чисел. Название происходит от лат. factorialis — действующий, производящий, умножающий;
- 5. Определение перестановки и пример В комбинаторике перестано́вка — это упорядоченный набор без повторений чисел 1,
- 6. Определение размещения и пример Размещением из m элементов по n называется любое упорядоченное подмножество из n
- 7. Определение комбинации и пример
- 8. Правило суммы и пример. Правило суммы. Если элемент А можно выбрать m способами, а элемент В
- 9. Правило произведения. Если элемент А можно выбрать m способами, а после этого элемент В – n
- 10. Задача 1 Из города А в город В ведут 3 дороги, из города В в город
- 11. Задача 2 Из города А в город В ведут 3 дороги, из города В в город
- 16. Скачать презентацию













 Основные направления истории моделирования
Основные направления истории моделирования Сравнительный анализ дизайна интернет-сайтов
Сравнительный анализ дизайна интернет-сайтов Персональные данные
Персональные данные Дональд Дэвис
Дональд Дэвис Помощь студенту к первой лабораторной работе. При выполнении лабораторных работ используется программа ISE Project Navigator
Помощь студенту к первой лабораторной работе. При выполнении лабораторных работ используется программа ISE Project Navigator Обработка графической информации. Вставка изображений в документы
Обработка графической информации. Вставка изображений в документы Объектно-ориентированные технологии программирования и стандарты проектирования
Объектно-ориентированные технологии программирования и стандарты проектирования Методы работы с источником информации
Методы работы с источником информации Информационные ресурсы
Информационные ресурсы Правила работы с презентацией
Правила работы с презентацией Алгоритм. Способы записи алгоритма
Алгоритм. Способы записи алгоритма Искусственный интеллект
Искусственный интеллект Поиск музыки по напеванию
Поиск музыки по напеванию Файл и файловая система
Файл и файловая система Байланыс негіздері
Байланыс негіздері Информационные технологии в гостиничном бизнесе
Информационные технологии в гостиничном бизнесе Сберкласс
Сберкласс Презентация на тему Информация и информационные процессы в технике
Презентация на тему Информация и информационные процессы в технике 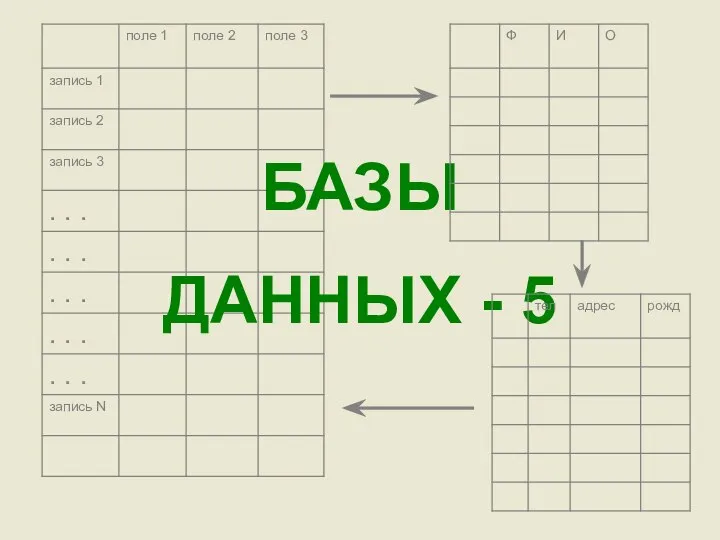 Базы данных - 5
Базы данных - 5 АО ТомскНИПИнефть: Общая информация об институте
АО ТомскНИПИнефть: Общая информация об институте Планерка. Семейство IG
Планерка. Семейство IG Премущества Интернета
Премущества Интернета Проект Преврати путешествие в киноленту
Проект Преврати путешествие в киноленту Обработка текстовых величин
Обработка текстовых величин Текстовые документы и технологии их создания обработка текстовой информации
Текстовые документы и технологии их создания обработка текстовой информации Среда программирования programming environment
Среда программирования programming environment Территориальные МИС (медицинская статистическая информация)
Территориальные МИС (медицинская статистическая информация) Информатика и я
Информатика и я