Компьютерные системы счисления

Система счисления - это знаковая система, в которой приняты определённые правила записи чисел.
Цифры - знаки, при помощи которых записываются числа.
Алфавит системы счисления - совокупность цифр.
Общие сведения
Простейшая и самая древняя система - унарная система счисления. В ней для записи любых чисел используется всего один символ - палочка, узелок, зарубка, камушек.
Система счисления называется непозиционной, если количественный эквивалент (количественное значение) цифры в числе не зависит от её положения в записи числа.
Система счисления называется позиционной, если количественный эквивалент цифры в числе зависит от её положения в записи числа.
Основание позиционной системы счисления равно количеству цифр, составляющих её алфавит.

Узловые числа обозначаются цифрами.
Узловые и алгоритмические числа
Римская система счисления

Цифры 1234567890 сложились в Индии около 400 г. н. э.
Арабы стали пользоваться подобной нумерацией около 800 г. н. э.
Примерно в 1200 г. н. э. эту нумерацию начали применять в Европе.
Десятичная система счисления

В позиционной системе счисления с основанием q любое число может быть представлено в виде:
Aq =±(an–1×qn–1+ an–2 × qn–2+…+ a0 × q0+ a–1×q–1+…+ a–m× q–m)
Здесь:
А — число;
q — основание системы счисления;
ai — цифры, принадлежащие алфавиту данной системы счисления;
n — количество целых разрядов числа;
m — количество дробных разрядов числа;
qi — «вес» i-го разряда.
Такая запись числа называется развёрнутой формой записи.
Основная формула

Aq =±(an–1 × qn–1+ an–2 × qn–2+…+ a0 × q0+ a–1 × q–1+…+ a–m × q–m)
Примеры записи чисел в развёрнутой форме:
2012=2×103 +0×102 +1×101 +2×100
0,125=1×10-1 +2×10-2 +5×10–3
14351,1=1×104 +4×103 +3×102 +5×101 +1×100 +1×10–1
Развёрнутая форма

Устное повторение:
Где применяется двоичная система счисления?
Каков ее алфавит и основание?
Как записать двоичное число в развернутой форме?

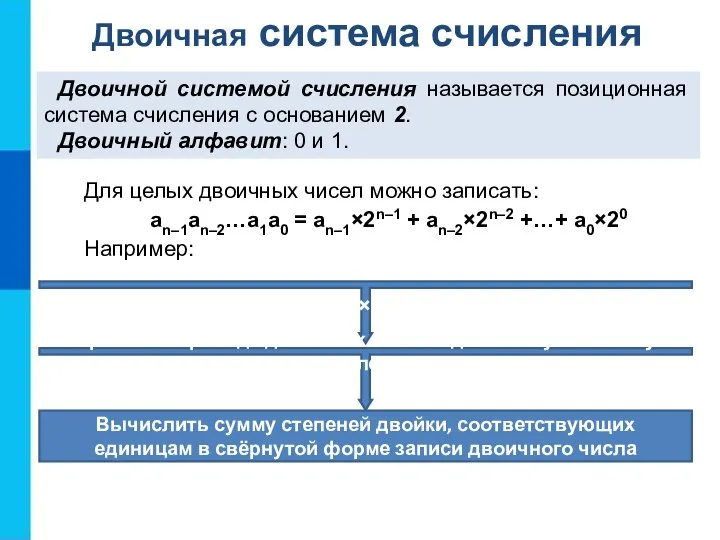
Двоичная система счисления
Двоичной системой счисления называется позиционная система счисления с основанием 2.
Двоичный алфавит: 0 и 1.
Для целых двоичных чисел можно записать:
an–1an–2…a1a0 = an–1×2n–1 + an–2×2n–2 +…+ a0×20
Например:
100112 =1×24+0×23+0×22+1×21+1×20 = 24 +21 + 20 =1910
Правило перевода двоичных чисел в десятичную систему счисления:
Вычислить сумму степеней двойки, соответствующих единицам в свёрнутой форме записи двоичного числа

Сколько разрядов памяти ПК займет двоичное число?
Придумай способ экономии места в памяти ПК.
73427037008
3B8B87C016
Свяжи цифры 8 и 16 с названием систем счисления.
1110111000101110000111110000002

«Компьютерные» системы счисления
Двоичная система используется в компьютерной технике, так как:
двоичные числа представляются в компьютере с помощью простых технических элементов с двумя устойчивыми состояниями;
представление информации посредством только двух состояний надёжно и помехоустойчиво;
двоичная арифметика наиболее проста;
существует математический аппарат, обеспечивающий логические преобразования двоичных данных.
Двоичный код удобен для компьютера.
Человеку неудобно пользоваться длинными и однородными кодами. Специалисты заменяют двоичные коды на величины в восьмеричной или шестнадцатеричной системах счисления.

an–1an–2…a1a0 = an–1×8n–1+an–2×8n–2+…+a0×80
Пример: 10638 =1×83 +0×82+6×81+3×80=56310.
Для перевода целого восьмеричного числа в десятичную систему счисления следует перейти к его развёрнутой записи и вычислить значение получившегося выражения.
Восьмеричная система счисления
Восьмеричной системой счисления называется позиционная система счисления с основанием 8.
Алфавит: 0, 1, 2, 3, 4, 5, 6, 7.
Основание: q = 16.
Алфавит: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F.
Шестнадцатеричная система счисления
3АF16 =3×162+10×161+15×160 =768+160+15=94310.

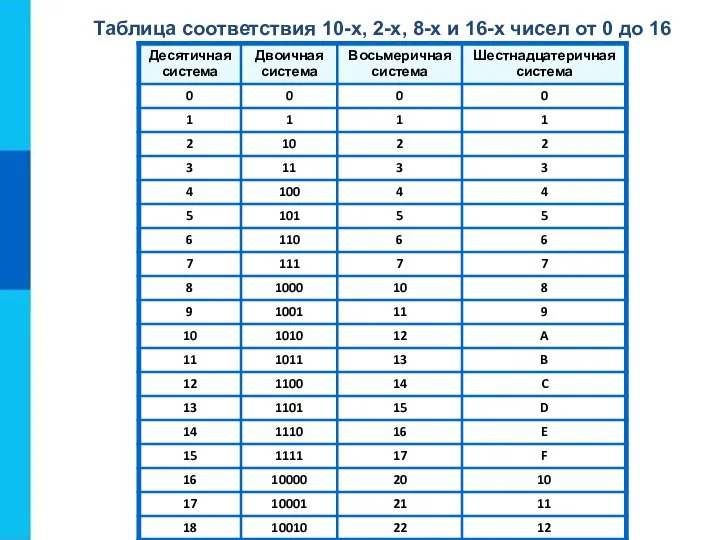
Таблица соответствия 10-х, 2-х, 8-х и 16-х чисел от 0 до 16

Задания для выполнения на уроке

Самостоятельно выполнить задания