Содержание
- 2. Оглавление: 1. Целые числа. 2. Ограничение, связанное с разрядностью архитектуры. 3. Представление целых чисел со знаком
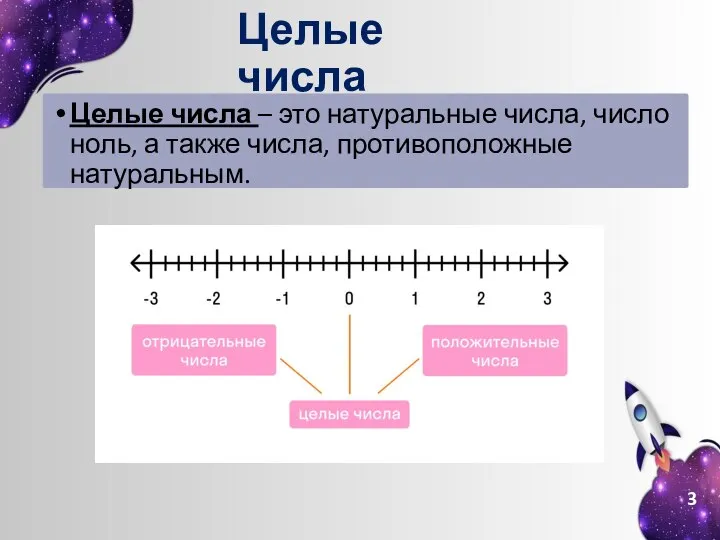
- 3. Целые числа Целые числа – это натуральные числа, число ноль, а также числа, противоположные натуральным.
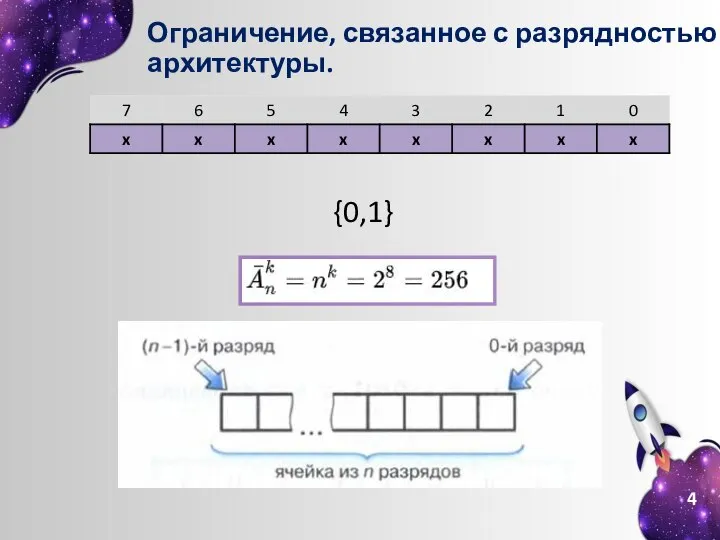
- 4. Ограничение, связанное с разрядностью архитектуры. {0,1}
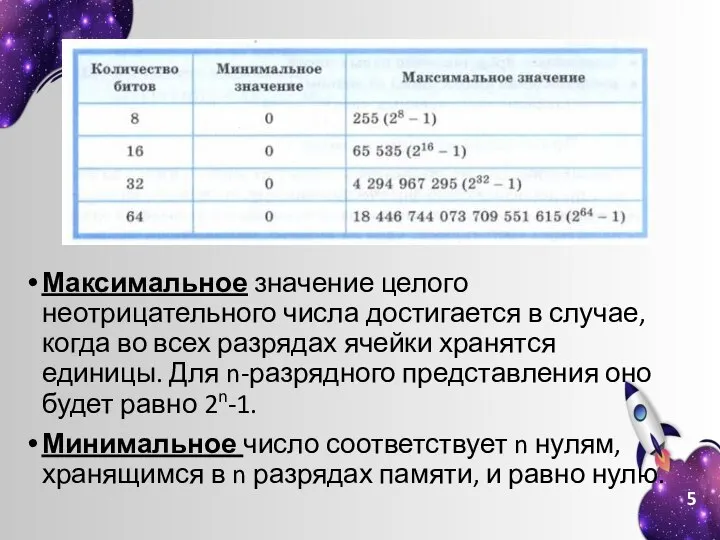
- 5. Максимальное значение целого неотрицательного числа достигается в случае, когда во всех разрядах ячейки хранятся единицы. Для
- 6. Пример: 1. Число 7210 = 10010002 в однобайтовом формате 2. Это же число в двубайтовом формате:
- 7. Представление целых чисел со знаком. Для представления знаковых целых чисел используются три способа: 1) прямой код;
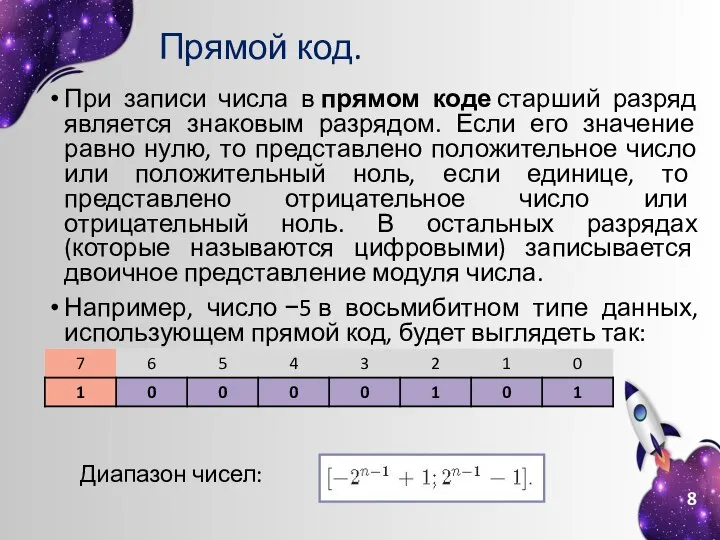
- 8. Прямой код. При записи числа в прямом коде старший разряд является знаковым разрядом. Если его значение
- 9. Схематичное представление прямого кода
- 10. Обратный код. Обратный код для положительного числа совпадает с прямым кодом. Для отрицательного числа все цифры
- 11. Дополнительный код Дополнительный код положительного числа совпадает с прямым кодом. Для отрицательного числа дополнительный код образуется
- 13. Операции «+» и «*» Сложение чисел без учёта знака
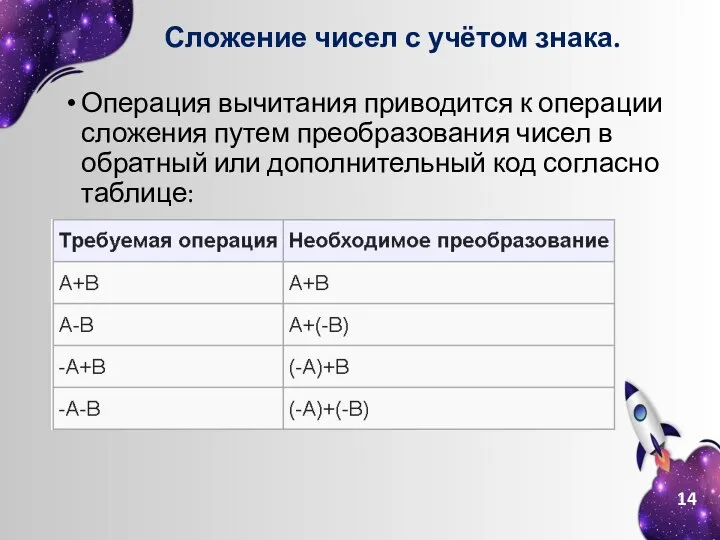
- 14. Сложение чисел с учётом знака. Операция вычитания приводится к операции сложения путем преобразования чисел в обратный
- 15. Сложение чисел со знаком в обратном коде. Сложение в обратном коде происходит следующим образом: по обычному
- 16. Сложение чисел со знаком в дополнительном коде. При алгебраическом сложении чисел со знаком результатом также является
- 17. Сложение чисел со знаком в дополнительном коде.
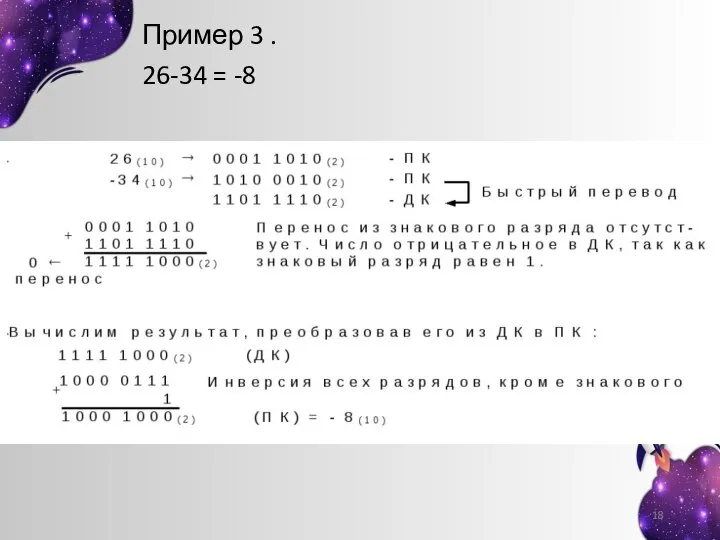
- 18. Пример 3 . 26-34 = -8
- 19. При сложении чисел в дополнительном коде единица переноса из старшего разряда игнорируется (теряется), а в обратном
- 20. Умножение Во многих компьютерах умножение производится как последовательность сложений и сдвигов. Результат инвертируем и прибавляем единицу
- 22. Скачать презентацию













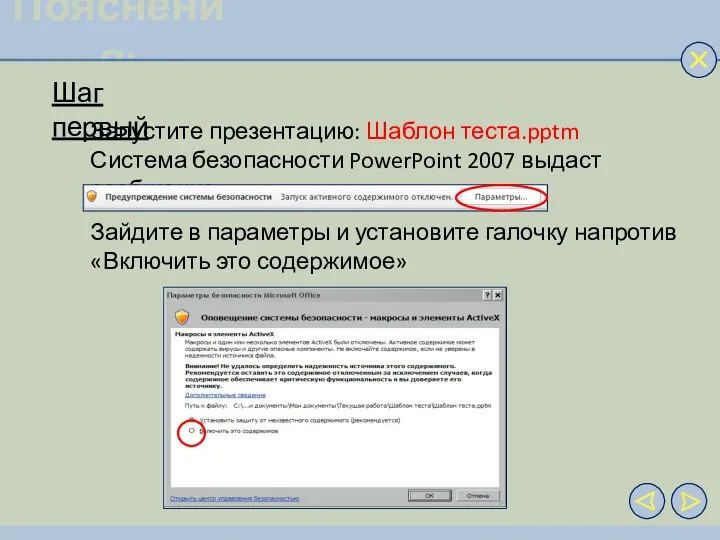 Шаблон теста
Шаблон теста Капитан Грантов. Лайфхаки грантрайтинга
Капитан Грантов. Лайфхаки грантрайтинга Віртуальні аудиторії Сумісна робота. Навчальні приміщення
Віртуальні аудиторії Сумісна робота. Навчальні приміщення Передача информации
Передача информации Файл. Внешняя память
Файл. Внешняя память Линейное программирование. Краски
Линейное программирование. Краски Конвергент от Ростелеком
Конвергент от Ростелеком История создания сети интернет. Резервное копирование и восстановление данных
История создания сети интернет. Резервное копирование и восстановление данных Исполнитель перемещайка
Исполнитель перемещайка программное обеспечение
программное обеспечение Тестирование и отладка программного средства
Тестирование и отладка программного средства Настройка INDIGO
Настройка INDIGO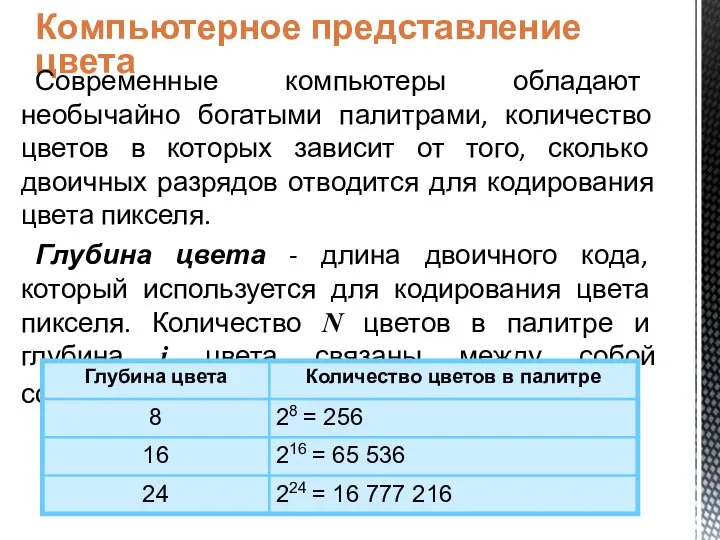 Компьютерное представление цвета
Компьютерное представление цвета Модели данных. Современные СУБД (Урок 2)
Модели данных. Современные СУБД (Урок 2) Интернет-зависимость и социокультурные предпосылки её возникновения
Интернет-зависимость и социокультурные предпосылки её возникновения lesson11
lesson11 Современные подходы к моделированию
Современные подходы к моделированию Анализ сетей массового обслуживания с положительными и отрицательными заявками
Анализ сетей массового обслуживания с положительными и отрицательными заявками The Kitik Times. Создание новостной, развлекательной интернет платформы, посвященной жизни животных
The Kitik Times. Создание новостной, развлекательной интернет платформы, посвященной жизни животных Обслуживание и диагностика EMC VNX
Обслуживание и диагностика EMC VNX Информационные ресурсы и технологии в менеджменте
Информационные ресурсы и технологии в менеджменте Автоматизированное тестирование UI
Автоматизированное тестирование UI Представление текстовой информации в ПК
Представление текстовой информации в ПК ВК: продвижение страницы
ВК: продвижение страницы Знакомство с интерфейсом программы Кумир
Знакомство с интерфейсом программы Кумир Презентация на тему Объект и его свойства
Презентация на тему Объект и его свойства  Индивидуальные сервисные пакеты
Индивидуальные сервисные пакеты Развитие персонажей
Развитие персонажей