Содержание
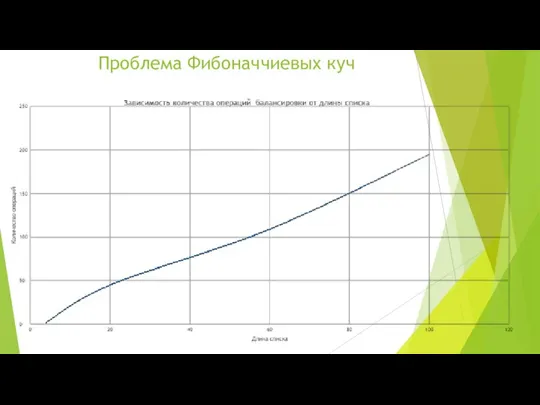
- 2. Проблема Фибоначчиевых куч
- 3. Структура 2-3 кучи Степень дерева – высота корневого узла Насыщенность дерева – возможность добавлять в дерево
- 4. Примеры деревьев Тип Внешний вид 2-3 дерева Общий внешний вид 1 1 2 1 3 2
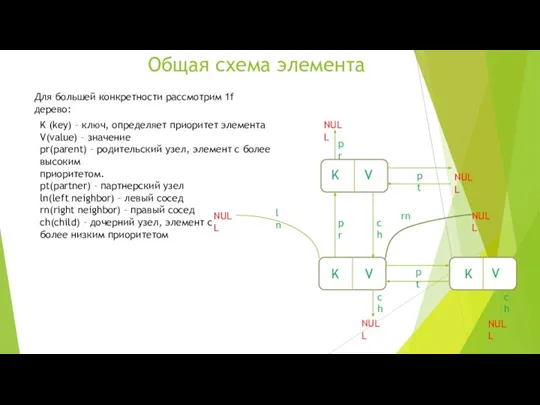
- 5. Общая схема элемента Для большей конкретности рассмотрим 1f дерево: NULL NULL NULL NULL NULL NULL K
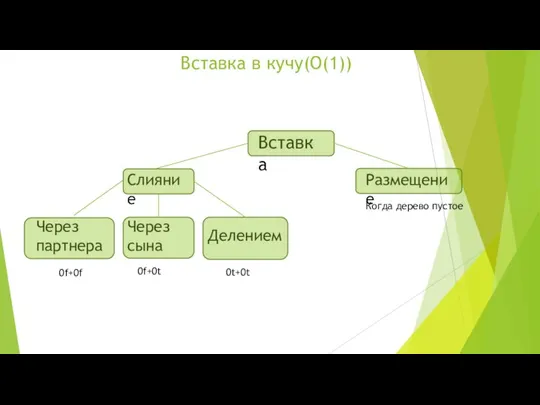
- 6. Вставка в кучу(O(1)) Вставка Размещение Слияние Через партнера Через сына Делением Когда дерево пустое 0f+0f 0f+0t
- 7. Пример вставки 1) Через партнера 1 2 1 2 + = 0f 0f 0t nf +
- 8. Извлечение из кучи минимума(O(log N)) Для извлечения из кучи минимума(это корневая вершина) сначала найдем нужное дерево,
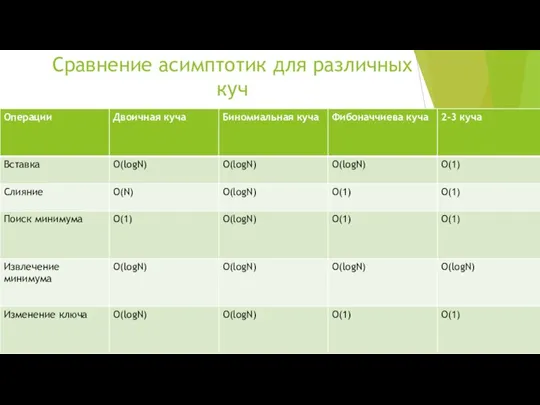
- 9. Сравнение асимптотик для различных куч
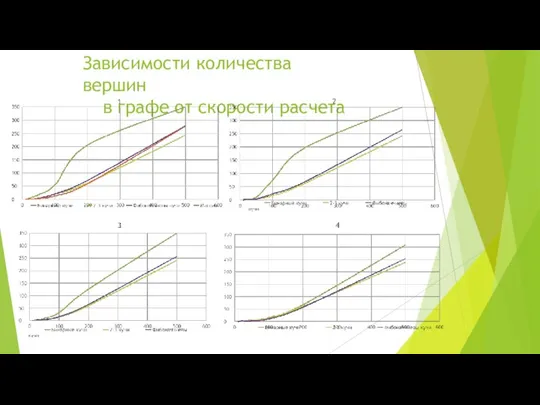
- 10. Зависимости количества вершин в графе от скорости расчета
- 12. Скачать презентацию




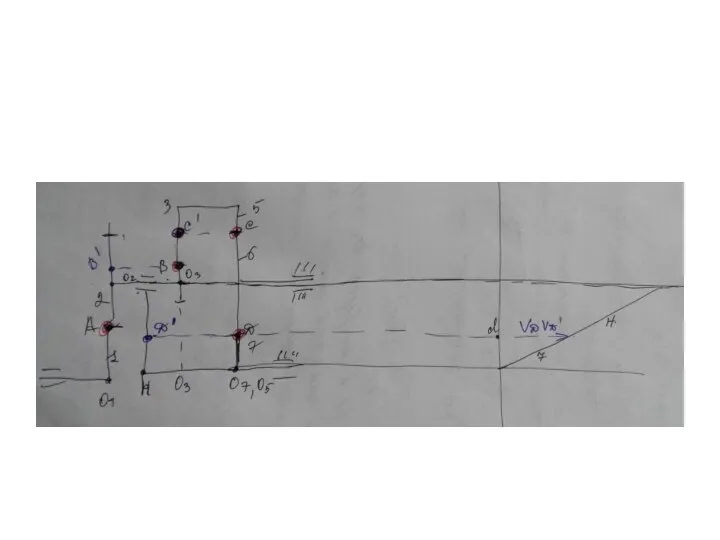 Схема
Схема Повторяющиеся элементы в окружающем мире. 6 класс
Повторяющиеся элементы в окружающем мире. 6 класс Анализ интернет-ресурсов
Анализ интернет-ресурсов Архитектура ЭВМ. Компьютерная память
Архитектура ЭВМ. Компьютерная память Интеграция с ФГИС Меркурий в типовых решениях 1С
Интеграция с ФГИС Меркурий в типовых решениях 1С Komanda FOR organizācija ciklisko izpildes citas komandas rezultāti, saraksti, un virknes teksta failus
Komanda FOR organizācija ciklisko izpildes citas komandas rezultāti, saraksti, un virknes teksta failus Практическая работа Шифрование данных
Практическая работа Шифрование данных Мифы о медийных личностях
Мифы о медийных личностях Алгоритмы. Вопросы
Алгоритмы. Вопросы Информационные технологии при изучении математики
Информационные технологии при изучении математики Настройка динамической маршрутизации на базе протокола RIP на ободуровании MikroTik
Настройка динамической маршрутизации на базе протокола RIP на ободуровании MikroTik Разработка электронного учебника по дисциплине Микропроцессоры
Разработка электронного учебника по дисциплине Микропроцессоры Разветвляющийся алгоритм
Разветвляющийся алгоритм Как мы познаём окружающий мир
Как мы познаём окружающий мир Bondder Landing page-Scroll down script
Bondder Landing page-Scroll down script Информатика. Информационные технологии
Информатика. Информационные технологии Классификация моделей и моделирования
Классификация моделей и моделирования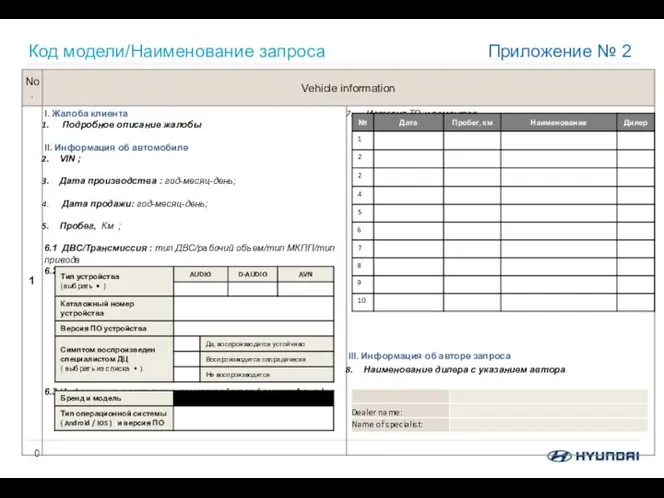 AVN_Hotline+_tech_issue+
AVN_Hotline+_tech_issue+ Поиск научной литературы, оценка достоверности и использование библиографических программ
Поиск научной литературы, оценка достоверности и использование библиографических программ Web-сайт, определение и классификация
Web-сайт, определение и классификация Формирование коммуникативно-языковой компетентности через внеурочные занятия по программе Hello English
Формирование коммуникативно-языковой компетентности через внеурочные занятия по программе Hello English Предметно-ориентированное проектирование автоматизированных систем управления. Раздел 2. Технологии DDD
Предметно-ориентированное проектирование автоматизированных систем управления. Раздел 2. Технологии DDD Безопасный интернет
Безопасный интернет Архитектура базы данных. Физическая и логическая независимость
Архитектура базы данных. Физическая и логическая независимость Microsoft Office. Краткая характеристика изученных программ
Microsoft Office. Краткая характеристика изученных программ OKauto - мобильное приложение в Казахстане, которое предоставляет сервис проверки, уведомления и оплаты штрафов ПДД
OKauto - мобильное приложение в Казахстане, которое предоставляет сервис проверки, уведомления и оплаты штрафов ПДД YouTube канал CryptoOptimist
YouTube канал CryptoOptimist Системное мышление
Системное мышление