Содержание
- 2. * MATLAB- это уникальная коллекция реализаций современных численных методов компьютерной математики. Вычисления, визуализация, программирование Возможности системы
- 3. MATLAB - уникальная коллекция реализаций современных вычислительных методов матричные и логические операторы элементарные и специальные функции
- 4. В области визуализации и графики: возможность создания двумерных и трехмерных графиков осуществление визуального анализа данных В
- 5. Список рекомендуемой литературы : Мартынов Н.Н. Matlab 7. Элементарное введение. -М:КУДИЦ-ОБРАЗ,2005.-416с
- 6. Список рекомендуемой литературы : Юлий Кетков, Александр Кетков, Михаил Шульц Matlab 7. Программирование, численные методы. -БХВ-Петербург,
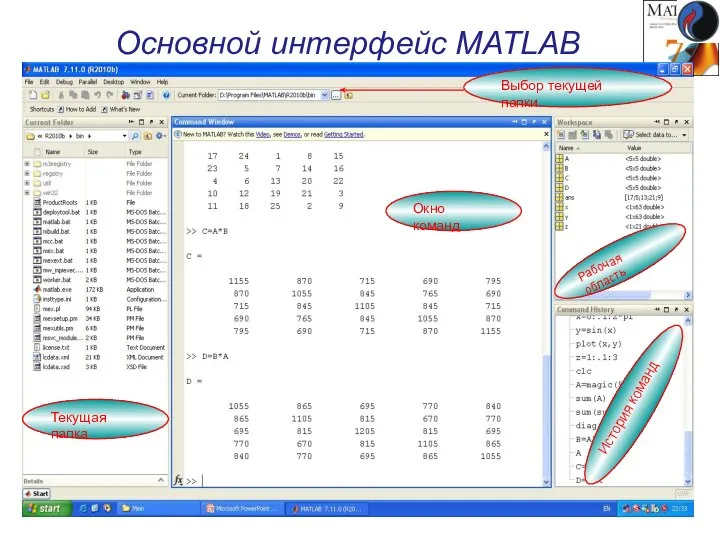
- 7. Основной интерфейс MATLAB Окно команд Рабочая область История команд Текущая папка Выбор текущей папки
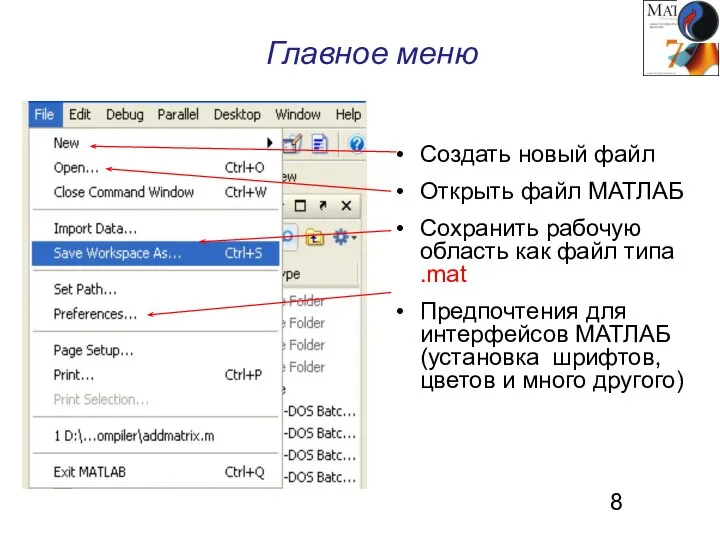
- 8. Главное меню Создать новый файл Открыть файл МАТЛАБ Сохранить рабочую область как файл типа .mat Предпочтения
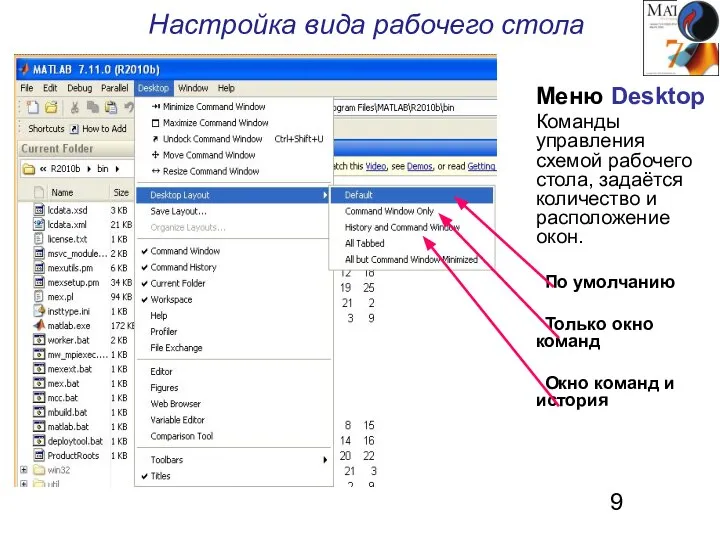
- 9. Настройка вида рабочего стола Меню Desktop Команды управления схемой рабочего стола, задаётся количество и расположение окон.
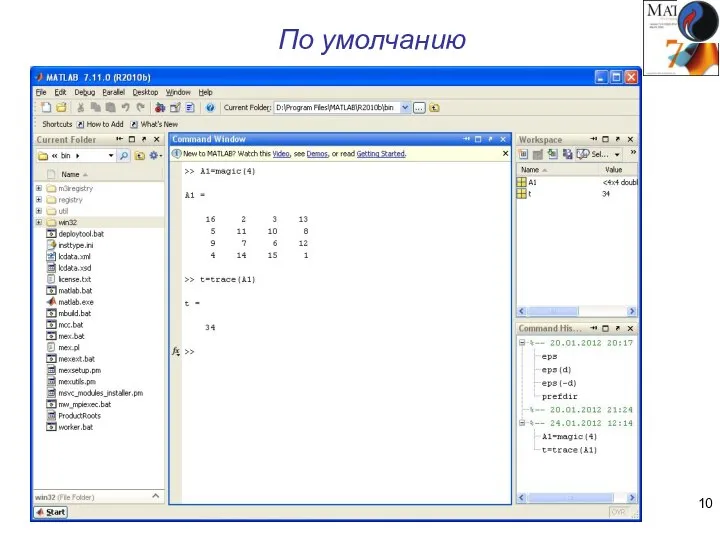
- 10. По умолчанию
- 11. В системе МАТЛАБ можно производить арифметические операции с действительными и комплексными числами, векторами и матрицами, вычислять
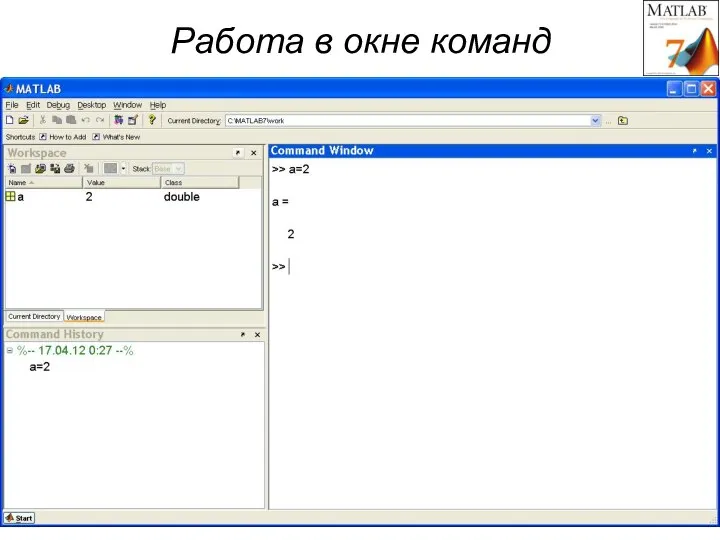
- 12. Работа в окне команд
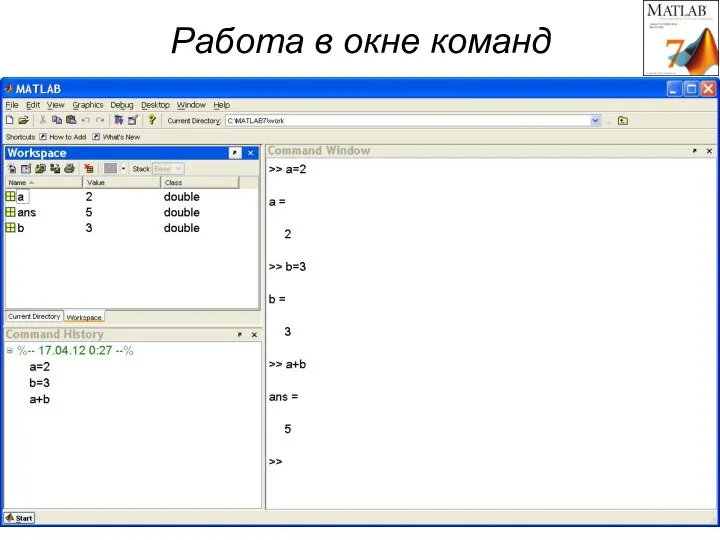
- 13. Работа в окне команд
- 14. Понятие M-файла Способы повторного ввода команд: 1. Использовать окно Command History 2. Применить m-файл m-файл может
- 15. M-файл (сценарий) Содержит серию команд, которые выполняются в режиме интерпретации построчно. Если в команде имеется ошибка,
- 16. Команды управления окном clc – очистки окна; who – вывод имен активных переменных; clear – удаление
- 17. Действительные и комплексные числа -68 3.4567 7.13e13 – означает 7.13*1013 1.7977е+308 – максимальное число realmax 2.2251e-308
- 18. Форматы format short – 4 цифры после точки (по умолчанию) format long – 15 цифр после
- 19. disp (‘Результаты расчета') Вывод комментария на экран Вывод значения а с точностью до 3 значащих цифр
- 20. Арифметические операторы Основные: + - * / ^ Обратное деление \ - справа налево Поэлементные: .*
- 21. В математических выражениях операторы имеют определенный приоритет исполнения. Например, в MATLAB приоритет логических операторов выше, чем
- 22. Элементарные алгебраические функции
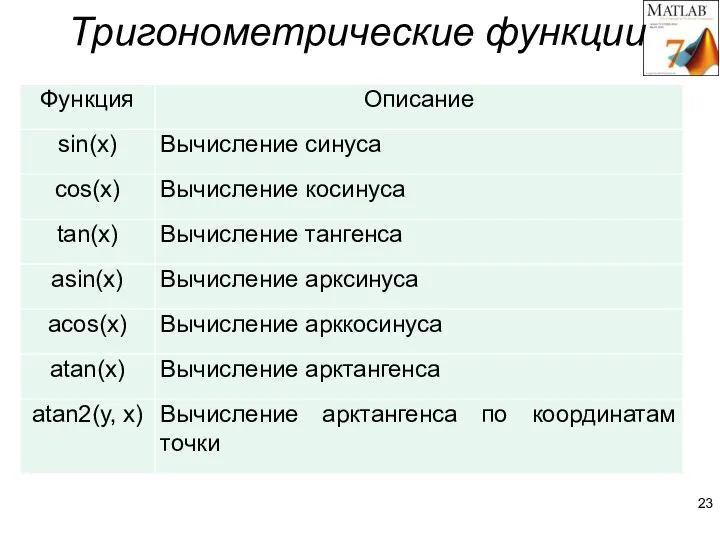
- 23. Тригонометрическиe функции
- 24. Результат вычислений присваивается переменной >> x=2-3^2 x = -7 >> x1=5*x x1 = -35 >> 1+1/2*4
- 25. Основной объект в системе Matlab — это матрицы, или массивы. Даже скалярные величины, рассматриваются системой как
- 26. Чтобы задать вектор, достаточно перечислить его элементы, заключая их в квадратные скобки. Элементы векторов-строк разделяются символами
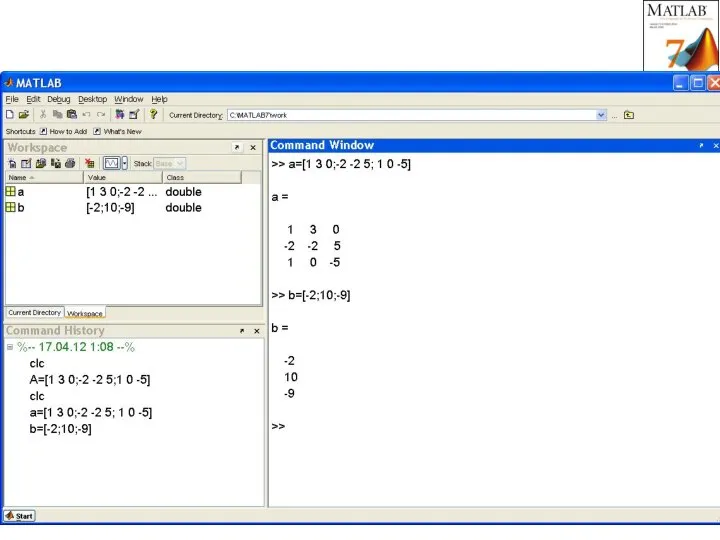
- 27. Одномерные массивы Задание массива: a = [ -3 4 2]; a = [ -3, 4, 2];
- 28. Двумерные массивы Задание массива: a = [ 1 2; 3 4; 5 6]; Доступ к элементу:
- 29. Диапазоны Функция magic(n) задает магическую матрицу nxn все ее элементы не превышают n2 Можно использовать как
- 30. for i=1:3 for j=1:3 if j>i – 1 a(i,j)=0.893+exp(2*j); else a(i,j)=2.914-sin(j*pi/i-i); end end end
- 31. Создание массивов со случайными элементами rand(n) и rand(m,n) генерируют матрицу (nxn) или (mxn) с элементами, распределенными
- 32. Диапазоны
- 33. Удаление строк и столбцов
- 34. Перестановка элементов
- 35. Операции над матрицами a+b сложение скаляров, векторов или матриц a−b вычитание скаляров, векторов или матриц a*b
- 36. Операции над матрицами Функция length(V) рассчитывает количество элементов в векторе V. Функция max(V) выдает значение максимального
- 37. Операции над матрицами Функция сортировки sort(V) формирует вектор, элементы которого распределены в порядке возрастания их значений.
- 38. Операции над матрицами abs(A) - модуль det(A) - определитель матрицы inv(A) - обратная матрица diag(A) -
- 39. Операции над матрицами prod(A,1) - произведение элементов массива в столбцах (по умолчанию prod(A)) prod(A,2) - произведение
- 40. Операции над матрицами sort(A) - сортировка по столбцам по возрастанию sort(A,2) -сортировка по строкам по возрастанию
- 41. Операции над матрицами [b2,INDEX]=sort(b) - возвращает отсортированный массив и массив индексов элементов в исходном массиве size(A)
- 42. Дневник работы Команда diary открывает дневник, т.е. указывает системе, что все, что появится после этой команды
- 43. Решение системы линейных уравнений. В матричном виде система имеет вид Ах =b, A , b ,
- 45. Решение системы линейных уравнений >> d=det(a) d = -5 >> x=А\b x = 1 -1 2
- 46. Решение системы линейных уравнений Решение x1=1, x2=-1, x3=2 легко проверить подстановкой в систему уравнений: >> disp(A*x)
- 48. Скачать презентацию


















![Одномерные массивы Задание массива: a = [ -3 4 2]; a =](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1096779/slide-26.jpg)
![Двумерные массивы Задание массива: a = [ 1 2; 3 4; 5 6]; Доступ к элементу:](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1096779/slide-27.jpg)












![Операции над матрицами [b2,INDEX]=sort(b) - возвращает отсортированный массив и массив индексов элементов](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1096779/slide-40.jpg)




 Турнир по Call of duty mobile
Турнир по Call of duty mobile Локальная сеть
Локальная сеть Пошаговая инструкция по работе с шаблонами в АИП Пилотный проект веб-портала НБ РК
Пошаговая инструкция по работе с шаблонами в АИП Пилотный проект веб-портала НБ РК Режимы построения объектов. Использование режимов ОРТО и ПОЛЯР
Режимы построения объектов. Использование режимов ОРТО и ПОЛЯР Операційні та файлові системи. Операційна система Windows XP Professional
Операційні та файлові системи. Операційна система Windows XP Professional Ближе к клиенту
Ближе к клиенту Инструкция по регистрации на курсе ПП
Инструкция по регистрации на курсе ПП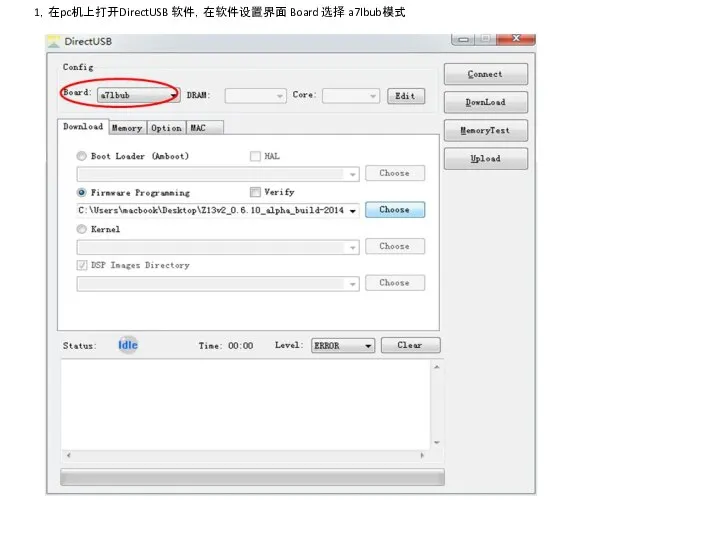 在pc机上打开 direct USB
在pc机上打开 direct USB Выбор валюты в документах внутреннего товародвижения
Выбор валюты в документах внутреннего товародвижения Склейка карт по фотографиям
Склейка карт по фотографиям Системы счисления
Системы счисления Алгоритмизация и программирование. Кафедра информатики Барнаул 2021
Алгоритмизация и программирование. Кафедра информатики Барнаул 2021 Комп'ютерні віруси
Комп'ютерні віруси Модуль. Модульная Сетка
Модуль. Модульная Сетка Администрирование СКЗИ
Администрирование СКЗИ Двумерные массивы
Двумерные массивы Основы моделирования схем в программе Electronics Workbench 512
Основы моделирования схем в программе Electronics Workbench 512 Разноцветные истории. Обзор альбомов отдела хранения основного фонда библиотеки
Разноцветные истории. Обзор альбомов отдела хранения основного фонда библиотеки Процедурное программирование 01_09_2021
Процедурное программирование 01_09_2021 Исследование топологии двумерных многообразий с помощью графического редактора Blender
Исследование топологии двумерных многообразий с помощью графического редактора Blender Массовая оптимизация запросов PostgreSQL – explain.sbis.ru
Массовая оптимизация запросов PostgreSQL – explain.sbis.ru Bakshaev
Bakshaev Классы. Описание класса
Классы. Описание класса Изучение работы программируемых логических контроллеров. Лабораторная работа №1
Изучение работы программируемых логических контроллеров. Лабораторная работа №1 Массивы в С#
Массивы в С# Компьютерные игры и сети как развлечение
Компьютерные игры и сети как развлечение İntellektual sistemlər
İntellektual sistemlər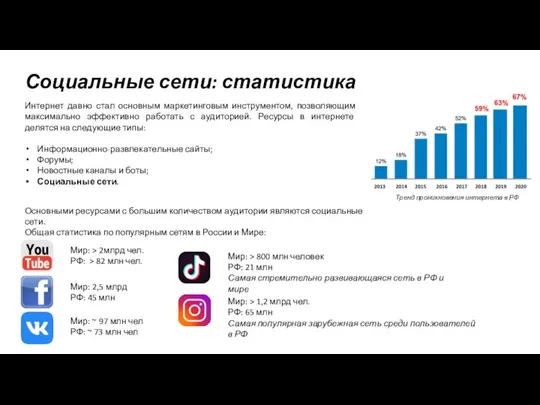 Социальные сети: статистика
Социальные сети: статистика